![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/ビットとバイナリー』として書籍化されています。
登場人物紹介
僕:数学が好きな高校生。
ミルカさん:数学が好きな高校生。僕のクラスメート。長い黒髪の《饒舌才媛》。
リサ:自在にプログラミングを行う無口な女子。赤い髪の《コンピュータ少女》。
ここは双倉図書館。
今日、僕はミルカさんに呼び出されてここにやってきた。
《変幻ピクセル》のイベントはもうとっくに終わったから、
何もないはずなんだけどな。
広いイベントホールに入ると、
大きなスクリーンにオセロを切り取ったような映像が映っていた。
白と黒の石がたくさん並び、くるくると白黒反転を繰り返している。

僕「何やってるの? ゲーム?」
ミルカ「おっと」
エラー音と共に ERROR! の文字が大きくスクリーンに表示された。

リサ「注意力不足」
ミルカ「ちょうどいい。彼も来たし、休憩にしよう」
僕「二人でゲームしていたの?」
ミルカ「いや、これは一人ゲーム。 フリップ・トリップだよ。 単純といえば単純なゲームだけど、おもしろい」
僕「フリップ・トリップ?」
ミルカ「私は《変幻ピクセル》に来れなかったからな(第103回参照)(第104回参照)。 君も参加できなかっただろう? リサに機材の一部をもう一度出してもらった。いっしょに遊ぼう」
リサ「迷惑」
僕「《変幻ピクセル》の話はユーリから聞いたよ(第107回参照)(第108回参照)。 リサちゃんからコンピュータのことたくさん教えてもらったって喜んでたよ。 ありがとう」
リサ「《ちゃん》は不要……大したこと、話してない(咳)」
僕「でも、フリップ・トリップとかいうゲームについては聞かなかったなあ。 これはどういうゲームなの?」
ミルカ「さっき私がやっていた《フリップ・トリップ $8$》は難しすぎるから、 《フリップ・トリップ $4$》にしよう」
リサ「説明パネル」
フリップ・トリップ(基本操作)

僕「ええと? まず、スタートボタンを押すと全部白になる、と」
スタートボタンを押した直後

僕「そして、反転ボタンを押したら、それに対応した石は白から黒になるんだね。 たとえば、反転ボタン $1$ を押すと、白白黒白ということかな」
スタートボタンを押して反転ボタン $1$ を押した

僕「そして反転ボタン $0$ を押すと、白白黒黒」
スタートボタン→反転ボタン $1$ →反転ボタン $0$
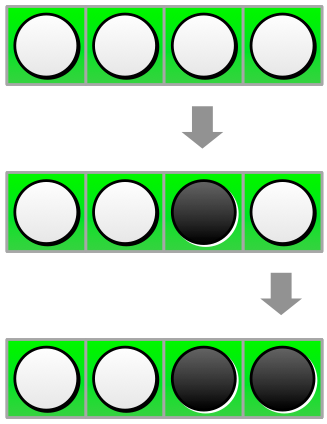
ミルカ「白なら黒になるが、黒なら白になる」
僕「ということは、もう一度ボタン $0$ を押すと、白白黒白に戻るんだね」
スタートボタン→反転ボタン $1$ →反転ボタン $0$ →反転ボタン $0$

僕が反転ボタン $0$ を押すと、 エラー音が響いてスクリーンにERROR!の文字が表示された。
ミルカ「同じパターンを出してしまったらエラーになる。 スタートしてから、白白黒白は出た。もう一度それを出したからエラーになった。 それがフリップ・トリップ」
リサ「説明パネル」
フリップ・トリップ(エラーとフルトリップ)

僕「過去に登場したパターンを作ってしまったらエラー……ということは、 同じパターンを作らないように反転ボタンを操作して、 全部のパターンを作るってこと?」
ミルカ「端的に言えば、そうなるな」
リサ「重複パターン禁止」
僕「うーん……そうか、 さっきは「白白白白→白白黒白→白白黒黒→白白黒白」と操作してしまったからエラーになったんだ。 白白黒白が二回出たから。 待てよ、 $4$ 個の石があって、それぞれ白黒二通りあるんだから、 全部で $16$ 個のパターンがある。 ということは、これまで出たパターンを最大 $16$ 個記憶しなくちゃいけないってことか」
ミルカ「まあ、記憶したければ」
僕「いやいや、簡単か。 だって、 $2$ 進法を使って数えるのと同じことをすればいいからね」
ミルカ「というと?」
僕「白を $0$ として、黒を $1$ として考えると、 $0000,0001,0010,0011,0100,0101,\ldots$ のように、 $2$ 進法で数を数えていくようにビットパターンを作っていけばいい。 そうすれば、 $4$ ビットのビットパターンすべてを尽くせるから……おっと! それじゃだめか」
ミルカ「だめだね」
$4$ ビットのビットパターン($2$ 進法で数えていく)
$$ \begin{array}{rcc} n & \REMTEXT{$n$のビットパターン} \\ \hline 0 & 0000 \\ 1 & 0001 \\ 2 & 0010 \\ 3 & 0011 \\ 4 & 0100 \\ 5 & 0101 \\ 6 & 0110 \\ 7 & 0111 \\ 8 & 1000 \\ 9 & 1001 \\ 10 & 1010 \\ 11 & 1011 \\ 12 & 1100 \\ 13 & 1101 \\ 14 & 1110 \\ 15 & 1111 \\ \end{array} $$
僕「そうだなあ。 反転ボタンを $1$ 回押すだけで、 $2$ 進法で $+1$ したビットパターンが作れるとは限らないからなあ…… $0000$ から $0001$ を作るのはいい。でも、 $0001$ から $0010$ を作るのはできない。 $0001$ から $0010$ を作ろうとすると、 $000\UL{1}$ と、 $00\UL{0}1$ の二つのビットを反転しなくちゃいけない。 でもたとえば、 $000\UL{1}$ のビットを反転したとたん、 $0000$ というビットパターンができてしまい……」
ミルカ「……そこでエラーになるわけだ」
僕「できないとは限らないか。 $000\UL{1}$ を先に反転するんじゃなく、 $00\UL{0}1$ を先に反転すればいけるかも……なるほどね。 このフリップ・トリップのポイントがやっとわかったよ。 $0000$ から $1111$ までのすべてのビットパターンを作るんだけど、 次のビットパターンに移るときには、 《過去のビットパターンと重ならない》ようにしつつ、 しかも《一度には $1$ ビットしか反転しちゃいけない》わけだね」
ミルカ「そういうこと」
僕「え……でも、そんなことできるのかな。 だって、フルトリップするためには、最後に $0000$ に戻らないといけないんだよね。 $1111$ から、 $1$ ビット反転で $0000$ にはいけないよ」
ミルカ「$2$ 進法に引きずられている。最後の一歩手前は $1111$ とは限らない。 ちょっとやってみせよう」
ミルカさんはそういうと、フリップ・トリップのスタートボタンを押し、 すごいスピードでボタンを押した。 $16$ 回の後、 $4$ 個の石はすべて白に戻り、 スクリーンにはFULL TRIP!と表示された。

僕「ううん……速すぎてわからなかったけど、 確かに《フルトリップ》を達成できそうなことはわかったよ」
問題
フリップ・トリップで、スタートボタンを押してから、 $3,2,1,0$ の四つの反転ボタンをどの順番で押せば、 フルトリップできるだろうか。

(読者のあなたも、考えてみませんか?)

無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2015年3月6日)
この記事は『数学ガールの秘密ノート/ビットとバイナリー』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!