第85回 シーズン9 エピソード5

ギザギザフレーク（前編）

図書室にて

僕「テトラちゃん、何を書いてるの？」

テトラ「あ、先輩！　いえ、あの、ちょっとうまく描けなくて……」

僕「何が？」

テトラ「これです」

僕「これは……何？」

テトラ「やっぱり、わからないですよね。 この本に描かれているKoch Snowflake（コッホ・スノーフレーク） …… 《コッホ雪片》という図形がきれいなので、 あたし、自分で描いてみたくなったんですが、すごく難しいんですっ！」

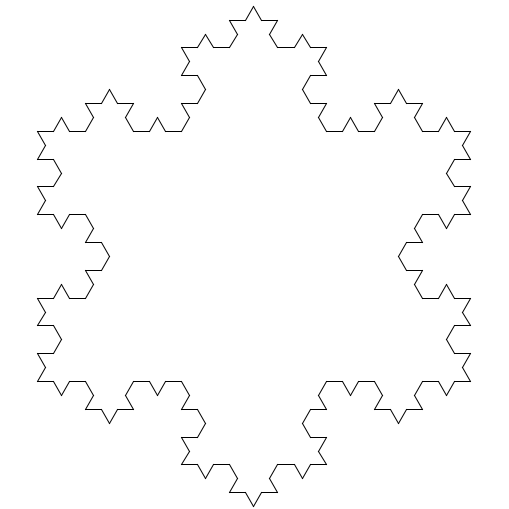
僕「ああ、これは見たことあるよ。フラクタルだね」

テトラ「フラクタル……そういえば、この本にもそんな言葉が出てきていました」

僕「うん、このコッホ雪片のような形の総称だよ。フラクタルは不思議な美しさがあるよね。 ちょっとギザギザして恐いところもあるけど。 ところで……テトラちゃんの描いたのとはずいぶん違うんじゃない？」

テトラ「え、ええっと……じゃあ、先輩も描いてみてくださいよぅ。 フリーハンドですからね。それから、この本、見ちゃだめですよ！」

僕「え、見ないで描くのか……うまく描けるかなあ」

テトラ「ね、先輩……意外と難しいですよね」

僕「そうだなあ。いや、でもほらテトラちゃんのよりは近いと思うけど。 少なくとも僕の方は線分に近い線で構成しているし」

テトラ「それは……確かに否定しませんが」

僕「ちょっと待って。これはちゃんと《構造》を調べてから描くべきだよ」

テトラ「構造といいますと？」

僕「この形はでたらめに作られたものじゃないよね。 何かルールがあって、それに従って作られたもの。だから、そのルールが作り出す構造を調べなくちゃ」

テトラ「なるほど。でも、この本にはあまり詳しく説明はないんです。 こういう図形がありますよとしか……」

僕「でも、ほらここに二つ例があるよ。だから、ここから考えてみようよ」

テトラ「はあ……」

僕「うん、思い出してきたよ。 以前フラクタルの本を読んだことがあるんだ。 そこに書いてあった」

テトラ「コッホ雪片の描き方ですか？」

僕「というか、フラクタルというものについて。 フラクタルのもっとも本質的な性質っていうのは、 《全体が部分と同じ形をしている》ということなんだ」

テトラ「全体が部分と同じ形をしている……」

僕「そうだね。このコッホ雪片の一辺《コッホ曲線》を切り出して考えてみるよ」

テトラ「はい。確かに似ている形といえばそうですが」

僕「ここをよく見ると、《似ている形》じゃなくて《同じ形》だってわかるよ」

テトラ「確かにそうですね！　左をぎゅっと小さくすると右と同じ形に！」

僕「フラクタルでは相似（そうじ）が大事な役割を果たすんだ。 ほら、拡大・縮小してぴったり重なる二つの図形は《互いに相似》っていうよね」

テトラ「はい」

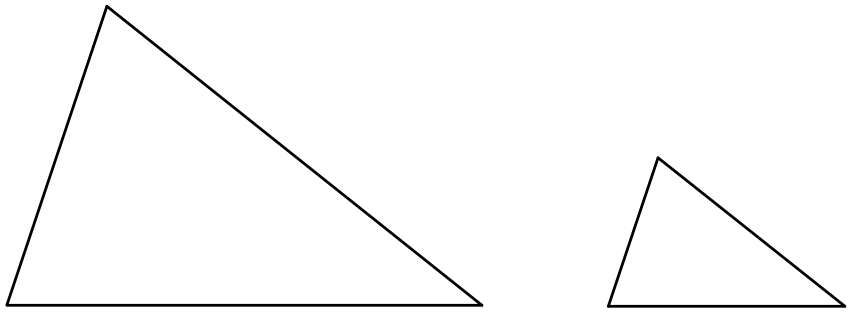
僕「だから、フラクタルというのは《全体が部分と相似になっている図形》といえるね」

テトラ「なるほど……あっ！　この斜めの部分も同じ形ですよね？　ちょっと傾いていますが。こっちも！　四つあります！」

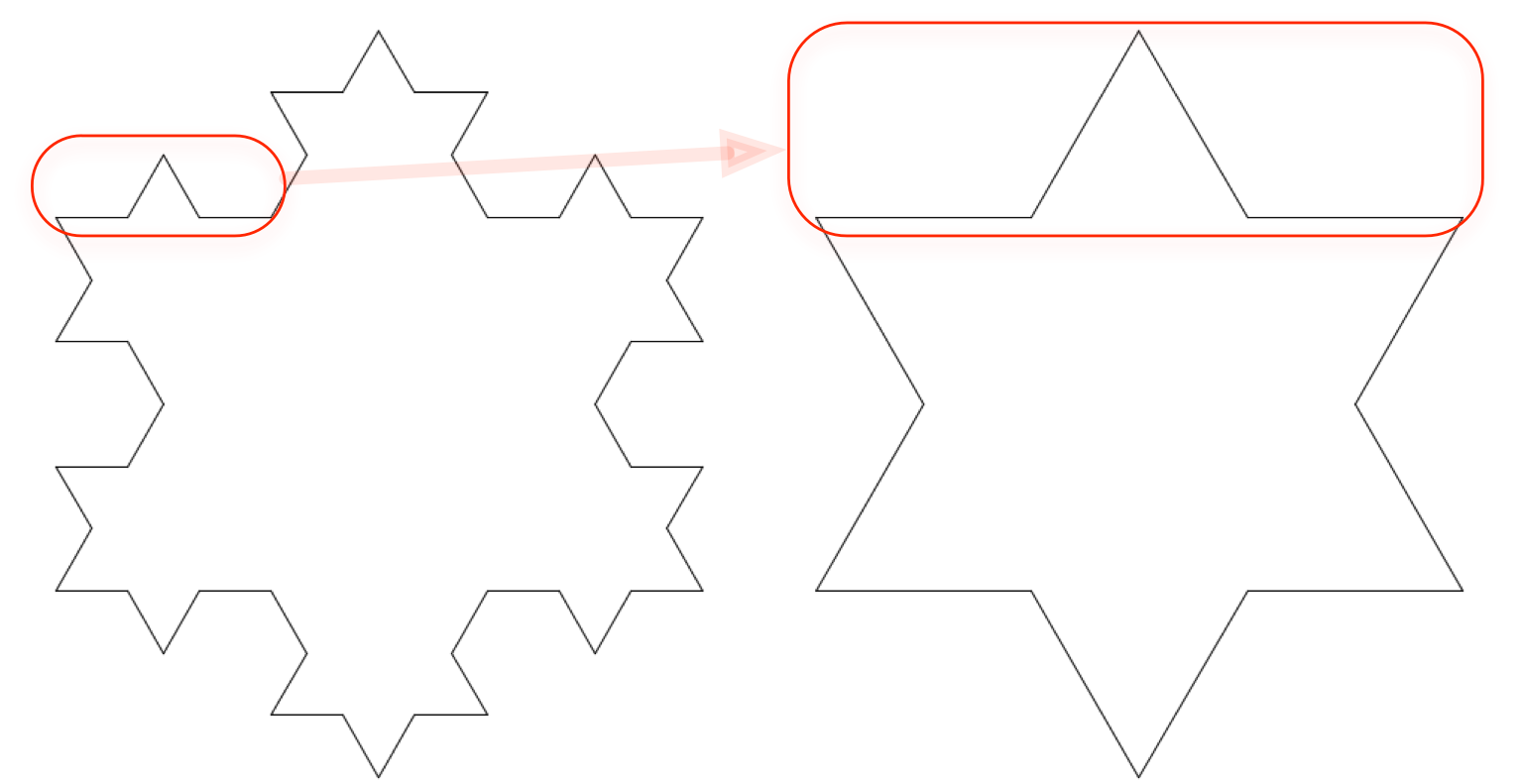
僕「うんうん、そうだね。 まんなかの出っ張りが正三角形だとすると、 $60$ 度の傾きを混ぜながら、辺を $4$ 本組み合わせていることになるね。 大ざっぱにいえば、これがコッホ曲線の構造といえるかな」

構造？

テトラ「ところで先輩。そもそも、構造っていうのはどういう意味なんでしょう」

僕「うん。構造っていうのはすごく意味が広い言葉だよ。 ミルカさんもよく構造やパターンという言い方をするね。 機械がいろんな部品を組み合わせてできるように、 基本的なものや形を組み合わせて、より複雑なものや形を作っているとき、 その組み合わせ方が構造といえるかな」

テトラ「組み合わせたり……あっ、分解したり？」

僕「うん、そうそう。いまコッホ曲線の構造を探っているのは、 まさに機械を分解しているような感じだね」

テトラ「そうですね」

僕「フラクタルのおもしろいところは、同じ構造が無限に続くってところにあるんだよ」

テトラ「無限に？」

僕「そうそう。さっきコッホ曲線を $4$ 個組み合わせて次のレベルのコッホ曲線を作ったけど、 できあがったコッホ曲線をさらに $4$ 個組み合わせて、さらに次のレベルを作ることもできるよね」

テトラ「ああっ、あああああっ！」

僕「どうしたの？！」

テトラ「す、すみません。想像したら、ものすごいイメージが浮かんでしまいまして……無限に続けたら、 ものすごく絡み合ってギザギザした丸い形になるんじゃないでしょうか」

僕「ギザギザした丸い形って……いや、そんなことないと思うよ。ほら、次のページにコッホ雪片の極限の形が載ってる」

テトラ「あ、あれ？　あまり丸くないですね」

僕「そうだね。全体としては正六角形の枠に収まるようなイメージかな。 雪の結晶に似ているといえば似ている」

テトラ「そうですね。それにしても、コッホ雪片を見ていると、なんだか引き込まれそうです。じっと見ていると《同じ形》があちこちに見つかってきて……」

僕「今度は、逆方向に行ってみよう」

テトラ「逆方向といいますと？」

僕「もっとシンプルな形。この一辺を取って、拡大して組み合わせればいいよね。一段階低いレベルのコッホ雪片が作れる」

テトラ「ははあ、そうですね。あっ、もう一回できますよ！」

僕「おもしろい！　一番低いレベルのコッホ雪片は $6$ 角形じゃなくて、 $3$ 角形なんだね！」

テトラ「全部並べてみます！」

テトラ「先ほど一辺を切り出して、縮小して $4$ 個並べたのを見てから、 何だか《形が見える》ような感じがします」

僕「そうだね。きっとそれが《構造を見抜く》ってことなんだよ」

テトラ「なるほどです」

ヒルベルト曲線

僕「その本、他にはフラクタルは載ってないの？」

テトラ「これはどうでしょう？　《ヒルベルト曲線》と書いてあります」