![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/場合の数』として書籍化されています。
今日は土曜日。ここは僕の家のダイニング。 ユーリと僕は組み合わせの数を題材に数学トークを続けている。
ユーリ「さすが数式マニア」
僕「マニアじゃないって」
ユーリ「でもね、お兄ちゃんが数式をいじっているときってすっごく楽しそーなんだよ」
僕「そうかなあ」
ユーリ「そーだよー。お兄ちゃん見てるとね、ユーリも数式書きたくなってくるもん」
僕「そりゃいいな……組み合わせの数といえば、ユーリはパスカルの三角形って知ってる?」
ユーリ「知ってるよー。上の二つを足して下の数作るんでしょ? お兄ちゃんもよく書いてくれたじゃん」
パスカルの三角形
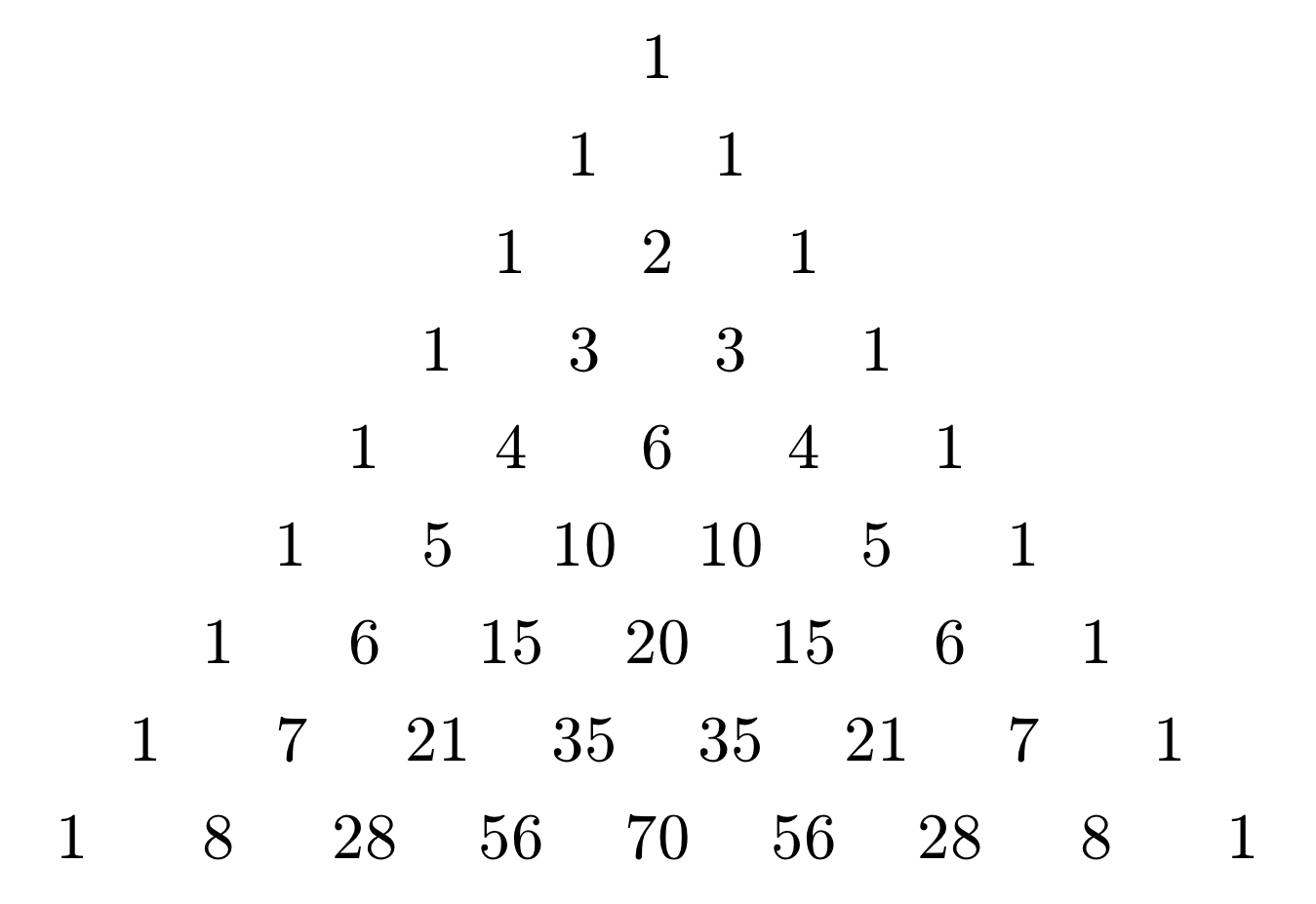
僕「うん。じゃあ、ここに出てくる数はぜんぶ組み合わせの数になるってことは知ってた?」
ユーリ「えーと……どこが?」
僕「こんなふうに表の形にした方がはっきりするかな」
表の形にしたパスカルの三角形

ユーリ「何がはっきりしたかわかんない」
僕「これだと《$n$ 行 $r$ 列目の数》が、ちょうど《$n$ 個のものから $r$ 個を取り出す組み合わせの数》になってるんだよ」
ユーリ「へー」
僕「たとえば、ほら、《$5$ 個のものから $2$ 個を取り出す組み合わせの数》を見てみると、 $\displaystyle\binom52 = \dfrac{5\times4}{2\times1} = 10$ だけど、 この表でもちゃんと《$5$ 行 $2$ 列目の数》は $10$ になってるだろ」
《$5$ 行 $2$ 列目の数》は $\binom{5}{2}$ に等しい

ユーリ「……ほんとだ。あ、この表って $0$ 行目から始まってるんだね」
僕「そうだよ。 $0$ から始めた方が便利だから」
ユーリ「へー」
僕「さっき(第67回参照)書いた《対称公式》も、 ちゃんとこの表の形にしたパスカルの三角形から読み取れるのがわかる?」
《対称公式》
$$ \displaystyle\binom{n}{r} = \binom{n}{n-r} $$
ユーリ「わかんない」
僕「《そのスピードは考えてない証拠》ってミルカさんから怒られたよね」
ユーリ「くっ……ミルカさまをダシに使うなー! ……えーとねー、 あ、そーか。行の数字が左右対称になってるってこと?」
僕「そうそう。 $1\,1$ や、 $1\,2\,1$ や、 $1\,3\,3\,1$ や……全部左右対称だね。 これを見ると確かに《対称公式》という名前がぴったり当てはまっている」
ユーリ「ふんふん」
僕「対称公式は組み合わせの定義から証明できたけど、 こんなふうにパスカルの三角形で見ることもできるし、 ユーリが言ってたように《$n$ 人から $r$ 人選ぶ》のは《$n$ 人から $n-r$ 人選ぶ》の同じと考えてもいいよね。 組み合わせの数はいろんな視点から見ることができるんだよ」
ユーリ「ほーほー」
僕「ところで、ユーリは不思議に思わない?」
ユーリ「何が?」
僕「パスカルの三角形は、 $0$ 行目に $1$ と書き、 $1$ 行目に $1\,1$ と書き、あとは上の行の $2$ 数を足し合わせて作るよね。 両端はいつも $1$」
ユーリ「そーだね」
パスカルの三角形の作り方

僕「どうしてこの作り方で組み合わせの数が出てくるんだと思う? こんなふうに $2$ 数を足し合わせるだけで」
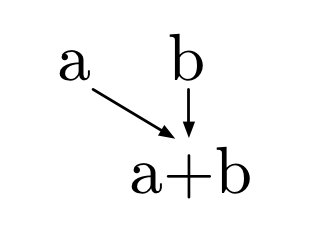
ユーリ「どーしてって……どーして?」
僕「パスカルの三角形はほんとに組み合わせの数を作るといえるのか。それが問題」
問題(パスカルの三角形と組み合わせの数)
パスカルの三角形は組み合わせの数を作るといえるか。
ユーリ「……わかんない。あっ、今度は考えたよ! そーじゃなくて、 わかんないってゆーのは、《どー答えていいか》がわかんないの」
僕「うん、そうだよね。こういう問題は《何をいえば答えたことになるか》がわかりにくいよね」
ユーリ「そーそー! 何をいったら答えたことになるの?」
僕「いくつか答え方はあると思うけれど、たとえば数式だけで答える方法がある」
ユーリ「数式で答える?」
僕「そう。パスカルの三角形の作り方は《両端は $1$ で、上の行の $2$ 数を加えて作る》といえるよね。簡単にいえば。 それに対して、組み合わせの数 $\displaystyle\binom{n}{r}$ は $\dfrac{n!}{r!\,\,(n-r)!}$ という式で定義できるよね」
ユーリ「うん、いーよ。それで?」
僕「だから、パスカルの三角形の作り方で、この組み合わせの数の式が出てくることを証明できればいいわけだ」
ユーリ「……」
僕「うん? わからない?」
ユーリ「ちょっと待って」
ユーリは急に真剣な顔になる。急速思考モードに入ったらしい。 栗色の髪が金色に変わる。 僕はそんなユーリが「こっちに戻ってくる」のをじっと待つ。
僕「……」
ユーリ「……ねー、お兄ちゃん」
僕「なに?」
ユーリ「うまくいえないんだけど……おもしろいね」
僕「なにが?」
ユーリ「あのね、パスカルの三角形は知ってたし、組み合わせの数になってると言われて『ふーん、そーかもね』と思ったよ。 でも、それを《証明しよう》とは思いもつかなかったの」
僕「うん」
ユーリ「でも考えてみればそーだよね。パスカルの三角形の作り方で、組み合わせの数ができるなんてすぐにわからないもん。 見た範囲……試したのは $\displaystyle\binom52$ だけだけど……は確かに組み合わせの数になってるみたい。 でもずっと先まで組み合わせの数になるなんて、そんな保証はないもんね」
僕「そうそう! そうなんだよ、ユーリ。偉いぞ。まさに、そのことのために証明をするんだ。 パスカルの三角形、ずっと下の、見えない先まで組み合わせの数になっているという保証のために」
ユーリ「できんの?」
僕「証明できるよ。ちょっと計算するだけだ」
ユーリ「教えて!」
僕「うん、これから僕たちが証明しようとしているのは、 $0$ 以上のすべての整数 $n$ と $r$(ただし、 $n \geqq r$)について、 表になったパスカルの三角形の《$n$ 行 $r$ 列目の数》が $\displaystyle\binom{n}{r}$ に等しいということ」
ユーリ「ふんふん。確かに、それが証明できれば、 パスカルの三角形が組み合わせの数になっているといえるもんね」
僕「話を簡単にするために、パスカルの三角形の《$n$ 行 $r$ 列目の数》のことを $T(n,r)$ と書くことにしよう」
ユーリ「?」
僕「こうすると、僕たちが証明したいことが式で表せる。 $0$ 以上のすべての整数 $n$ と $r$(ただし、 $n \geqq r$)について、 $T(n,r) = \displaystyle\binom{n}{r}$ を証明すればいいんだ!」
$$ T(n,r) = \dfrac{n!}{r!\,\,(n-r)!} $$
ユーリ「にゃるほど!」
僕「試しに考えてみよう。 $T(0,0)$ の値は何だろう」
ユーリ「《$0$ 行 $0$ 列目》の数ってことだよね? $1$ だよ、表で見ると」
僕「うん。そして $\dfrac{n!}{r!\,\,(n-r)!} = \dfrac{0!}{0!\,\,(0-0)!} = 1$ だから、こっちも $1$ になってる。 $T(0,0) = \displaystyle\binom{0}{0}$ は成り立っている。 言い換えると $n = 0, r = 0$ のとき $T(n,r) = \displaystyle\binom{n}{r}$ は成り立つ」
ユーリ「先は長いにゃ」
僕「次に、特別な $n$ と $r$ について考えてみよう」
ユーリ「特別?」
僕「各行の《両端》を考える。つまり $r = 0$ のときと、 $n = r$ のとき」
ユーリ「えーと……あ! 絶対 $1$ になるところ?」
僕「そうそう。パスカルの三角形では $r = 0$ のときと、 $n = r$ のときは必ず $1$ になる。 つまり $T(n,0) = 1$ と $T(n,n) = 1$ がいえる。 それなら、組み合わせの数の定義では?」
ユーリ「$r = 0$ のときは、 $\dfrac{n!}{r!\,\,(n-r)!} = \dfrac{n!}{0!\,\,(n-0)!} = \dfrac{n!}{n!} = 1$ だから、 $1$ だね!」
僕「その通り。だから、 $T(n,0) = \displaystyle\binom{n}{0}$ はいつも成り立つ。 $n = r$ のときはどうだろう?」
ユーリ「$n = r$ のときは、 $\dfrac{n!}{r!\,\,(n-r)!} = \dfrac{n!}{n!\,\,(n-n)!} = \dfrac{n!}{n!} = 1$ だから、やっぱり $1$ だよ!」
僕「いいね! これで $T(n,n) = \displaystyle\binom{n}{n}$ も成り立つことがわかった」
ユーリ「でもさー、これってパスカルの三角形の端っこの $1$ だけじゃん? かんじんの表の中の方は……どーすんの?」
僕「パスカルの三角形の作り方の通りにすればいいんだよ。作り方、知ってるだろ?」
ユーリ「上の行の $2$ 数を足すんだけど、その通りにするって、どーゆーこと?」
僕「正確に言おう。《$n$ 行 $r$ 列目の数 $T(n,r)$》と《$n$ 行 $r+1$ 列目の数 $T(n,r+1)$》を足したら《$n+1$ 行 $r+1$ 列目の数 $T(n+1,r+1)$》に等しくなるってことだね」
ユーリ「そっかな」
僕「つまり、パスカルの三角形では、 $$ T(n,r) + T(n,r+1) = T(n+1,r+1) $$ が成り立っている。 だから、組み合わせの数 $\displaystyle\binom{n}{r}$ でも同じ式が成り立つかどうかを調べればいい」
この式は成り立つか?
$$ \binom{n}{r} + \binom{n}{r+1} = \binom{n+1}{r+1} $$
ただし、 $n$ と $r$ は $0$ 以上の整数で $n \geqq r$ とする。
ユーリ「おー! そっか! ……って、お兄ちゃんごめん、これってどーするの?」
僕「え? 組み合わせの定義の式を使って計算するんだよ。やってみよう。 ごちゃごちゃするけど、分数の足し算だから、通分して足すだけだよ」
$$ \begin{align*} & \binom{n}{r} + \binom{n}{r+1} \\ &= \dfrac{n!}{r!\,\,(n-r)!} + \dfrac{n!}{(r+1)!\,\,(n-(r+1))!} \qquad \textbf{組み合わせの数の定義から} \\ &= \dfrac{(r+1) \times n!}{(r+1) \times r!\,\,(n-r)!} + \dfrac{(n-r) \times n!}{(n-r) \times (r+1)!\,\,(n-(r+1))!} \qquad \textbf{通分} \\ &= \dfrac{(r+1) \times n!}{(r+1)! \,\, (n-r)!} + \dfrac{(n-r) \times n!}{(r+1)! \,\, (n-r)!} \qquad \textbf{分母を計算した} \\ &= \dfrac{(r+1) \times n! + (n-r) \times n!}{(r+1)!\,\,(n-r)!} \qquad \textbf{加えた} \\ &= \dfrac{((r+1) + (n-r)) \times n!}{(r+1)! \,\, (n-r)!} \qquad \textbf{$n!$でくくった} \\ &= \dfrac{(n+1) \times n!}{(r+1)! \,\, (n-r)!} \qquad \textbf{$((r+1) + (n-r)) = n+1$だから} \\ &= \dfrac{(n+1)!}{(r+1)! \,\, (n-r)!} \qquad \textbf{$(n+1) \times n! = (n+1)!$だから} \\ &= \binom{n+1}{r+1} \qquad \textbf{組み合わせの数の定義から} \\ \end{align*} $$
ユーリ「うわあ、ややこしー! 通分が通分に見えない!」
僕「$(r+1) \times r! = (r+1)!$ と $(n-r) \times (n-r-1)! = (n-r)!$ に気付く必要があるからなあ。 そして最後に $(n+1) \times n! = (n+1)!$ もね。ぜんぶ階乗の取り扱いだけど」
ユーリ「ややこしーけど、計算できるんだ!」
僕「だから、結局これが成り立つ」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2014年3月7日)
この記事は『数学ガールの秘密ノート/場合の数』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!