![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/場合の数』として書籍化されています。
ここは僕の高校の屋上。いまはお昼休み。 僕とテトラちゃんは、《握手問題》を一緒に考えていた。 ようやく漸化式までたどりついたところ。
※以下では、組み合わせの個数${}_m\textrm{C}_n$を$\displaystyle\binom{m}{n}$と表記します。
問題2($2n$ 人の握手問題)[条件補足]
$2n$ 人の人が円形に並んでいます($n = 1,2,3,\ldots$)。 全員が、誰か一人と握手をします。 このとき《握手の仕方》は何通りありますか。
ただし、一つの握手は他人同士の握手と交差してはいけないとします。
僕「……だから、一般の $a_n$ について、こんな漸化式が書けそうだ」
$$ a_{n+1} = a_na_0 + a_{n-1}a_1 + a_{n-2}a_2 + \cdots + a_2a_{n-2} + a_1a_{n-1} + a_0a_n $$テトラ「あ、あの……」
僕「シグマを使って簡単に書けば、こうだね……おっと! 思い出した!」
$a_n$ が満たす漸化式
$$ a_{n+1} = \sum_{k=0}^{n} a_{n-k}a_k $$
テトラ「先輩?」
僕「うわあ! なぜここまで気付かなかったんだろう! ねえテトラちゃん、 これは有名な数列だよ。カタラン数だ」
テトラ「カタラン数……名前があるんですか」
僕「うん。カタラン数の一般項なら覚えているよ。第 $n$ 項を $C_n$ と書くことにすると、 $\displaystyle C_n = \dfrac{1}{n+1}\binom{2n}{n}$ になるはず。計算してみよう」
カタラン数の一般項 $C_n$
$$ C_n = \dfrac{1}{n+1}\binom{2n}{n} \qquad (n = 0,1,2,3,\ldots) $$
テトラ「そ、そうなんですか。でも……」
僕「実際に計算してみようよ」
$C_0$ を計算する
$$ \begin{align*} C_0 &= \dfrac{1}{n+1}\binom{2n}{n} \qquad \textbf{カタラン数の定義から} \\ &= \dfrac{1}{0+1}\binom{2\cdot 0}{0} \qquad \textbf{$n = 0$とした} \\ &= \dfrac{1}{1} \binom{0}{0} \qquad \textbf{} \\ &= 1 \cdot 1 \qquad \textbf{} \\ &= 1 \\ \end{align*} $$
$C_1$ を計算する
$$ \begin{align*} C_1 &= \dfrac{1}{n+1}\binom{2n}{n} \qquad \textbf{カタラン数の定義から} \\ &= \dfrac{1}{1+1}\binom{2\cdot 1}{1} \qquad \textbf{$n = 1$とした} \\ &= \dfrac{1}{2} \binom{2}{1} \qquad \textbf{} \\ &= \dfrac{1}{2} \cdot \dfrac{2}{1} \qquad \textbf{} \\ &= 1 \\ \end{align*} $$
$C_2$ を計算する
$$ \begin{align*} C_2 &= \dfrac{1}{n+1}\binom{2n}{n} \qquad \textbf{カタラン数の定義から} \\ &= \dfrac{1}{2+1}\binom{2\cdot 2}{2} \qquad \textbf{$n = 2$とした} \\ &= \dfrac{1}{3} \binom{4}{2} \qquad \textbf{} \\ &= \dfrac{1}{3} \cdot \dfrac{4\cdot 3}{2 \cdot 1} \qquad \textbf{} \\ &= \dfrac{6}{3} \\ &= 2 \\ \end{align*} $$
$C_3$ を計算する
$$ \begin{align*} C_3 &= \dfrac{1}{n+1}\binom{2n}{n} \qquad \textbf{カタラン数の定義から} \\ &= \dfrac{1}{3+1}\binom{2\cdot 3}{3} \qquad \textbf{$n = 3$とした} \\ &= \dfrac{1}{4} \binom{6}{3} \qquad \textbf{} \\ &= \dfrac{1}{4} \cdot \dfrac{6 \cdot 5 \cdot 4}{3 \cdot 2 \cdot 1} \qquad \textbf{} \\ &= \dfrac{20}{4} \\ &= 5 \\ \end{align*} $$
$C_4$ を計算する
$$ \begin{align*} C_4 &= \dfrac{1}{n+1}\binom{2n}{n} \qquad \textbf{カタラン数の定義から} \\ &= \dfrac{1}{4+1}\binom{2\cdot 4}{4} \qquad \textbf{$n = 4$とした} \\ &= \dfrac{1}{5} \binom{8}{4} \qquad \textbf{} \\ &= \dfrac{1}{5} \cdot \dfrac{8 \cdot 7 \cdot 6 \cdot 5}{4 \cdot 3 \cdot 2 \cdot 1} \qquad \textbf{} \\ &= \dfrac{70}{5} \\ &= 14 \\ \end{align*} $$
テトラ「ははあ……確かに、 $1, 1, 2, 5, 14$ ということは $C_n$ と $a_n$ は同じ数列……なんでしょうか」
僕「そうだよ。さっき作った数列の表に追加しよう。 $n = 0$ も含めて……(第65回参照)」
《握手の仕方》の数列 $a_n$
$2n$ 人の《握手の仕方》の数を $a_n$ で表そう($n = 0,1,2,3,\ldots$ とする)。
これまでにわかった $a_n$ を表に書く。カタラン数 $C_n$ も追加する。
$$ \begin{array}{c|ccccccc} n & 0 & 1 & 2 & 3 & 4 & \cdots \\ \hline \REMTEXT{人数$2n$} & 0 & 2 & 4 & 6 & 8 & \cdots \\ \hline a_n & 1 & 1 & 2 & 5 & 14 & \cdots \\ \hline C_n & 1 & 1 & 2 & 5 & 14 & \cdots \\ \end{array} $$
テトラ「確かにここまで一致しますが、 先輩……でも、どうして急にカタラン数という数列を思い出したんですか?」
僕「うん、この漸化式だよ。正確には $a_0 = 1$ を付け加えた漸化式。 この漸化式に見覚えがあったんだ」
$a_n$ が満たす漸化式
$$ \left\{\begin{array}{llll} a_{0} & = 1 \\ a_{n+1} & = \sum_{k=0}^{n} a_{n-k}a_k \qquad (n = 0,1,2,3,\ldots) \\ \end{array}\right. $$
テトラ「こんな複雑な式に?」
僕「そうそう、この漸化式を元に、母関数(ぼかんすう)という方法を使って一般項を求めたんだ。 自分で考えたから記憶に残っていたのかな。 といっても、ミルカさんと二人で解いたんだけど」
テトラ「ミルカさんと……お二人で」
僕「そうだね」
テトラ「そうですよね。お二人ならば解けますよね。いくら難しい方法でも。その……ええと、母関数という方法で」
僕「いや、母関数を使わなくても、いったん一般項 $a_n$ が $\displaystyle\dfrac{1}{n+1}\binom{2n}{n}$ という式で表されると 予想ができたなら、証明はすぐにできるよ。数学的帰納法を使えばいいんだから。母関数を使わなきゃいけないわけじゃない」
テトラ「予想がつけばそうかもしれませんが……そもそも、こんな式は思いつきません!」
午後の授業の予鈴が鳴った。 昼休み終了だ。
【CM】
ユーリ「突然ですが、ここでCMです! ミルカさまとお兄ちゃんがいっしょにカタラン数に
立ち向かう場面は『数学ガール』第一巻に登場しますので、
未読の方はどーぞ。Kindle版も出ましたー!」
放課後、僕は「数列 $a_n$ の漸化式から 一般項 $\displaystyle\dfrac{1}{n+1}\binom{2n}{n}$ が得られる」ことの証明を行おうと取り組んでいた。 しかし……なかなかうまくいかない。 「予想ができれば数学的帰納法を使えばいい」と言ったけれど、 そんなに簡単ではないようだな。
そこにミルカさんとテトラちゃんがいっしょに話しながらやってきた。
テトラ「……そうなんですか、ミルカさん」
ミルカ「そう。母関数を使わなくても一般項は求められる」
僕「何の話?」
テトラ「もちろん、お昼の《握手問題》です! ミルカさんも母関数を使わなくてもいいと」
僕「ああ、カタラン数を求めるときに、 以前ミルカさんが教えてくれた、曲がり角の……」
ミルカ「それとは別の話。 場合の数を求めるときには《問題の言い換え》が大事になる」
僕「それはそうだね」
テトラ「問題の言い換え……といいますと」
ミルカ「場合の数を数えるとき、 数えやすいように問題を言い換えるのだ。 もちろん、問題の構造が変わるような言い換えはできないが」
テトラ「すみません……よくわかりません」
ミルカ「カタラン数は非常にたくさんの言い換えが可能だ」
僕「曲がり角の……」
ミルカ「それもそうだが、別の話をしよう。《数えやすいように問題を言い換える》というのは、 《もれなく、だぶりなく》数えるように問題を変形するともいえるし、 問題が含んでいる構造を明らかにするともいえる。 だから《数えやすいように問題を言い換える》のは、数学的示唆に富むことも多い」
テトラ「そうなんですか……」
ミルカ「テトラが提示した握手から始めよう。 $n = 2$ つまり $2n = 4$ 人で握手している状況を想像する」
テトラ「はい、二通りあります」

ミルカ「円形に並んでいると考えにくいので、一列に並んでもらう。 握手としては不自然になるけれど意味はわかるだろう。 これは《数えやすいように問題を言い換える》ことの一つだ」
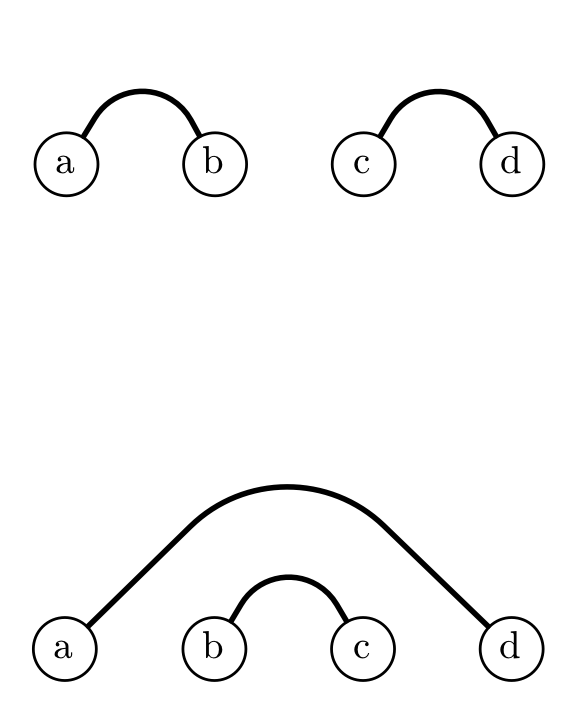
テトラ「え……あ、わかります。aさんとdさんは手をぐうんと伸ばしているのですね」

ミルカ「ここで、握手を表す線を矢印だと考えることにする。 矢印は左から右に向かうことにすれば、場合の数は増えも減りもしない。 これも《数えやすいように問題を言い換える》ことになる」

テトラ「はい、わかってきました! 言い換えてはいますが、 問題の大事なところは変わっていないから、 場合の数は変わらないということですね」
ミルカ「そう」
僕「確かに場合の数は変わらないけれど、 数えやすくもなっていないよね」
ミルカ「まだ話は終わっていない」
僕「……」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2014年2月21日)
この記事は『数学ガールの秘密ノート/場合の数』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!