![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/場合の数』として書籍化されています。
ユーリ「ミルカさまの受け売りはいいから」
僕「別に受け売りってわけじゃないんだけどね」
僕は高校二年生。いとこのユーリは中学二年生。 僕たちはいっしょに数学を題材におしゃべりをしている。 クイズやパズルを楽しむような感覚だ。 ユーリはあまり根気強くはないけど、なかなか賢い。
ユーリ「『なかなか賢い』じゃなくて『とっても賢い』だよ!」
僕「地の文に突っ込むなよ」
ユーリ「それにしても、突然 $2$ 進数が出てくるのはおもしろいにゃ」
僕「まあそうだよね。《集合》はいろんな分野の土台になっているし」
ユーリ「いろんな分野って?」
僕「たとえば幾何学。数学の幾何学では、直線や円のような図形を扱うよね」
ユーリ「三角形とか?」
僕「そうそう。図形は《点》が集まったものと見なすことができる。 つまり《図形は点の集合》ということ」
ユーリ「ほーほー、なるほど。それで?」
僕「だから、集合の考え方を使って、図形を扱うことができる。集合は幾何学の土台になっているといえる」
ユーリ「あんましピンと来ない」
僕「そう? たとえば、球面を考えたとする。ボールの表面を想像すればいいよね。シャボン玉の表面でもいい」
ユーリ「きゅうめん? いいよ」
僕「それを平面で切ったとしよう。大きな包丁でさくっと」
ユーリ「ぱぁん!」
僕「うわ! 急に大声出すなよ」
ユーリ「だってボールに包丁入れたら破裂するし」
僕「あ……まあね。ボールはたとえだよ。球面を平面で切ると、その断面は円になる」
ユーリ「わかるよん」
僕「その円は、《球面を作っている点の集合》と《平面を作っている点の集合》の二つの集合の《共通部分》になるわけだ」
ユーリ「きょうつうぶぶん」
僕「そう。さっき説明したよね。共通部分というのは、二つの集合の両方に属している要素の集合のこと(第63回参照)」
ユーリ「両方、ね」
僕「そう。《球面を作っている点であり》かつ《平面を作っている点でもある》……そんな点の集合のこと」
ユーリ「なんか、わざわざめんどくさく説明してるよーな気もするけど」
僕「幾何学だけじゃない。集合の考え方は、連立方程式を解くときも出てくるよ」
ユーリ「へー」
僕「連立方程式を解くときは、二つ以上の方程式を連立させて解くけど、 あれはそれぞれの方程式の《解の集合》の《共通部分》を求めていることになる」
ユーリ「あ、また共通部分」
僕「そうだね。……集合の考え方は数学のあちこちに登場するんだよ」
ユーリ「……」
僕「どうした?」
ユーリ「話、もどっちゃうんだけど、気になった」
僕「何が?」
ユーリ「さっきの《球面》を《平面》で切る話。ボールと包丁」
僕「?」
ユーリ「お兄ちゃんはさっき、《球面を作っている点の集合》と《平面を作っている点の集合》の《共通部分》は円になるっていってたけど、 そうじゃないときもあるよね。なんてゆーか、こう……ぎりぎりピタッと」
僕「そうだね! その通りだよ。ユーリは球面と平面が接するときのことを言ってるんだね。ユーリは賢いなあ。 球面が平面に接しているときは、共通部分はたった一点からなる集合になるね。その一点は接点になる」
ユーリ「でしょー? だから円になるときもあるけど、点になるときもあるよね?」
僕「そうそう。まあ、一点を《半径が $0$ の円》と見なして、も……」
ユーリ「お兄ちゃん、どしたの。顔赤いよ」
僕「いや、何でもないよ。一点を《半径が $0$ の円》と見なすこともできるけどね」
ユーリ「あと、空振りするときもある」
僕「空振りって?」
ユーリ「ほら、ボールを切ろうとしたけど、包丁空振りでスカッと」
僕「そうだね。球面と平面の共通部分が空集合になるときだね」
ユーリ「あ、そっか。そー言えるんだ」
僕「こんなふうに、集合の言葉は数学のいろんな概念を整理して表現できるんだよ」
ユーリ「ところでさ、お兄ちゃん。あのね、さっきヴェン図のパターンをたくさん数えたじゃん?(第63回参照)」
僕「そうだね」
ユーリ「小学校のとき、あれと似たような図で別な計算をしたことある」
僕「どういう計算?」
ユーリ「あのね、チョコとクッキーの好きな人の数の問題。たとえば、こんな感じの問題」
問題(チョコとクッキー)
教室にいる $30$ 人の生徒にチョコとクッキーの好き嫌いを聞いたところ、 全員が好きか嫌いかのどちらかを答えてくれました。
チョコが好きな人は $21$ 人いました。
クッキーが好きな人は $14$ 人いました。
どちらも嫌いな人は $5$ 人いました。(信じらんない!)
チョコとクッキーの両方が好きな人は何人いますか。
僕「なるほど、なるほど……」
ユーリ「えっと、いま適当に作ったんだけど、お兄ちゃんわかる?」
僕「わかるよ。図を描いて考えればわかるけど……《教室にいる人の集合》と《チョコが好きな人の集合》と《クッキーが好きな人の集合》を こんなふうに描く。ヴェン図だね」

ユーリ「ふんふん」
僕「この問題文からわかるのは、こうだね」
《(a)教室にいるのが $30$ 人》
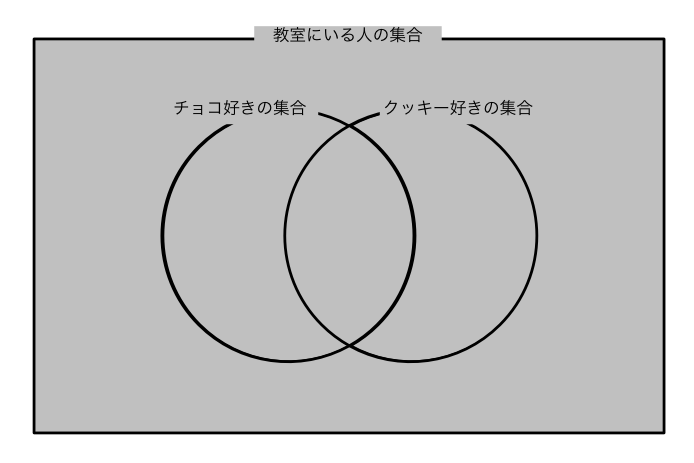
《(b)チョコが好きな人が $21$ 人》

《(c)クッキーが好きな人は $14$ 人》
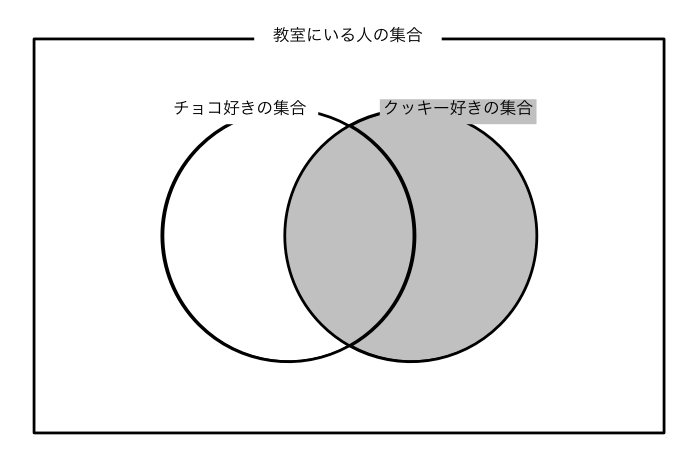
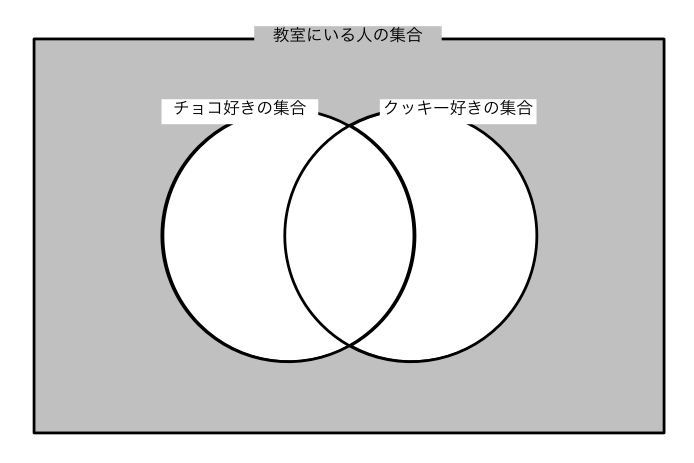
ユーリ「そーだね」
僕「チョコ好き($21$ 人)と、クッキー好き($14$ 人)と、どちらも嫌い($5$ 人)を足すと、 $21 + 14 + 5 = 40$ になって、教室にいる人($30$ 人)を $10$ 人も越えてしまう。 なぜ越えてしまうかというと……」
ユーリ「両方好きな人をだぶって数えてるから!」
僕「そうそう。だからその越えた $10$ 人がちょうど両方好きな人の人数になるんだね」
解答(チョコとクッキー)
チョコとクッキーの両方が好きな人の人数は $10$ 人になります。
ユーリ「まー、そんな感じで、こーゆー計算を思い出したの」
僕「なるほど」
ユーリ「でもね、小学生だったけど、ユーリ、すごくなっとくいかなかった」
僕「何が?」
ユーリ「あのね。先生が『チョコ好きな人』って言ったんだけど、 ほんとは『チョコ好きな人で、この中にはクッキーが好きな人も嫌いな人もいるよ』って言ってほしかったんだよ」
僕「なるほど」
ユーリ「何だかね、先生に引っ掛けられたような気がしたの」
僕「うん、ユーリの気持ちはちょっとわかるかも」
ユーリ「なんてゆーか……もうちょっとちゃんと言ってくれたら答えられたのに」
僕「まちがったの?」
ユーリ「うん……最初、かんちがいして、『チョコ好きな人』を『チョコだけが好きな人』って意味だと思ってまちがった」
僕「なるほど。言葉だけで説明するとそうなっちゃうね、確かに」
ユーリ「ってゆーか……うーん、先生って、ていねいに教えてくれるんだと思ってたのに、 なんだかひっかけられたような気持ちになったの。 かっこいい先生だったのに、すんごくがっかりした」
僕「小学校のとき?」
ユーリ「……小学校のとき」
僕「それは……ごめんな、ユーリ」
ユーリ「なんで、お兄ちゃんがあやまんの?」
僕「いや、なんとなく」
ユーリ「……ま、いーや! とにかく、こーゆー集合の問題ではヴェン図を考えればまちがえないよねっ!」
僕「そうだね……そうか」
ユーリ「どしたの?」
僕「いや、ユーリがいうのは正しい。とても正しい。 いま、集合に属する要素の数を数えたんだけど、そういうときにヴェン図を描いて考えるのはとても正しい態度だよ」
ユーリ「え、だからそーゆー話、してたんだよね?」
僕「うん。お兄ちゃんが考えてたのは、それを数式で書く方法について」
ユーリ「?」
僕「要素の数を数えること。つまりね、 全体の人数、 チョコが好きな人数、クッキーが好きな人数、チョコとクッキーの両方が好きな人数、両方とも嫌いな人数……その人数の関係は 一般的に数式で書けるなあと考えてたんだよ」
ユーリ「なに言ってるのかわかんない」
僕「こういう数式のこと!」
$$ \begin{align*} & \textbf{《全体の人数》} + \textbf{《両方が好きな人数》}\\ &= \textbf{《チョコが好きな人数》} + \textbf{《クッキーが好きな人数》} + \textbf{《両方とも嫌いな人数》} \\ \end{align*} $$
ユーリ「え?」
僕「いや、こう書いた方が自然かなあ」
$$ \begin{align*} & \textbf{《全体の人数》} - \textbf{《両方とも嫌いな人数》}\\ &= \textbf{《チョコが好きな人数》} + \textbf{《クッキーが好きな人数》} - \textbf{《両方が好きな人数》} \\ \end{align*} $$
ユーリ「え? ……えーと。全体から両方嫌いな人数引いて、うわめんどくさい」
僕「いやいや、ちゃんと読んでほしいな」
ユーリ「はいはいっと。全体から両方嫌いな人数を引いて……うん、なるほど、そっか《チョコとクッキーとどっちかは好きな人数》てこと?」
僕「そうだね」
ユーリ「で、それはチョコ好きとクッキー好きを足してから、両方好きを引く……あったりまえじゃん!」
僕「だよね。当たり前だ」
ユーリ「これって、あれでしょ? 丸いの二つ足しておいて、重なったアーモンド部分を引いたんでしょ?」
僕「そうそう、よく分かってるね」
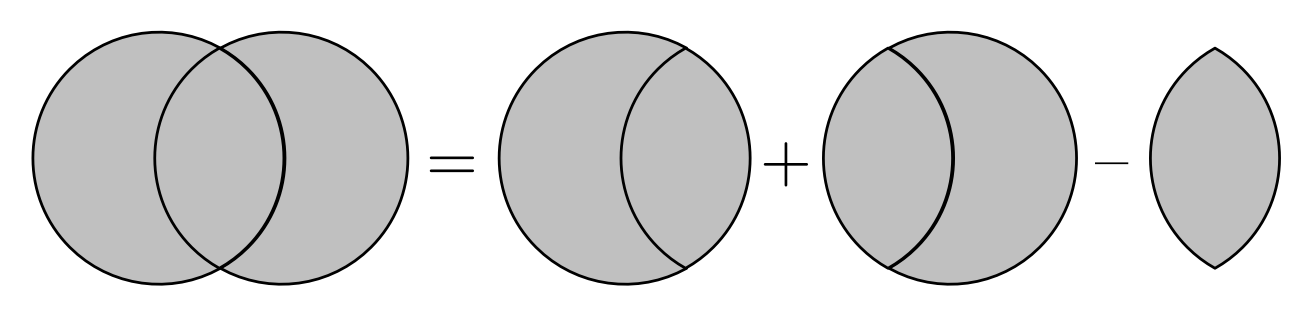
ユーリ「カンタン、カンタン」
僕「ユーリが言い換えた通り、こう書いてもいいね」
$$ \begin{align*} & \textbf{《チョコとクッキーの少なくとも片方が好きな人数》}\\ &= \textbf{《チョコが好きな人数》} + \textbf{《クッキーが好きな人数》} - \textbf{《両方が好きな人数》} \\ \end{align*} $$

ユーリ「カンタン、カンタン……それにしてもお兄ちゃんって数式好きだね」
僕「数式になると安心するんだよ」
ユーリ「変なの」
僕「変じゃないよ。数式で書けると、『確かにわかった』って感じるんだ」
ユーリ「ふーん」
僕「でもね、さっきの式はまだ日本語を使っていたから、長ったらしくなっているよね。 文字と記号を使って書けば、ずっと短く、ずっと簡単に書ける」
ユーリ「へー、たとえば?」
僕「《チョコが好きな人の集合》を $A$ として、 《クッキーが好きな人の集合》を $B$ と書く。これは文字を使って表したわけだね」
ユーリ「あははっ、そりゃ短くなるよね。一文字だもん」
僕「そして、 $A$ と $B$ の少なくとも片方に属している要素の集合……つまり《$A$ と $B$ の和集合》のことを、 $A \cup B$ と書くことにしよう」
$A$ と $B$ の和集合
$$ A \cup B $$
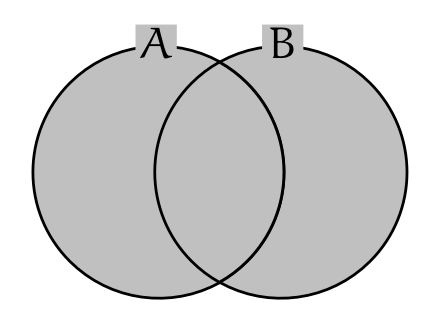
ユーリ「あ、これ、どっかで見たことある。お兄ちゃんが前に教えてくれたんだっけ?」
僕「そうだったかな」
ユーリ「すっごくまぎらわしーんだよ、この記号」
僕「そう? この記号 $\cup$ はカップみたいな形をしてるよね。 $A$ と $B$ を合わせてすくい上げるんだよ」
ユーリ「$A$ と $B$ を合わせてすくい上げるカップ……ふーん」
僕「そして、別の記号。 $A$ と $B$ の両方に属している要素の集合……つまり《$A$ と $B$ の共通部分》のことを、 $A \cap B$ と書くんだ」
$A$ と $B$ の共通部分
$$ A \cap B $$

ユーリ「ほらきた。まぎらわしーんだよね。 $\cup$ だか $\cap$ だか」
僕「何回か書いていると、すぐに慣れるよ」
ユーリ「そーゆーもん?」
僕「そういうもの。それで、集合 $A$ に属している要素の個数を $|A|$ で表すことにする」
集合 $A$ の要素の個数
$$ |A| $$
ユーリ「要素の個数って……チョコ好きな人数のこと?」
僕「そう。《チョコ好きな人の集合》を $A$ で表したとき、《チョコ好きの人数》は $|A|$ と書ける」
ユーリ「めんどくさいね」
僕「最初はね。でも、こういうふうに約束事を決めておきさえすれば、後がすごく楽になる。 とても複雑なことが短く表せるから。めんどくさくなくなるんだよ」
ユーリ「へー」
僕「たとえばさっきの《チョコとクッキーの少なくとも片方が好きな人数》の式は、 ズバリ、こう書ける」
集合の要素数の関係式
$$ |A \cup B| = |A| + |B| - |A \cap B| $$
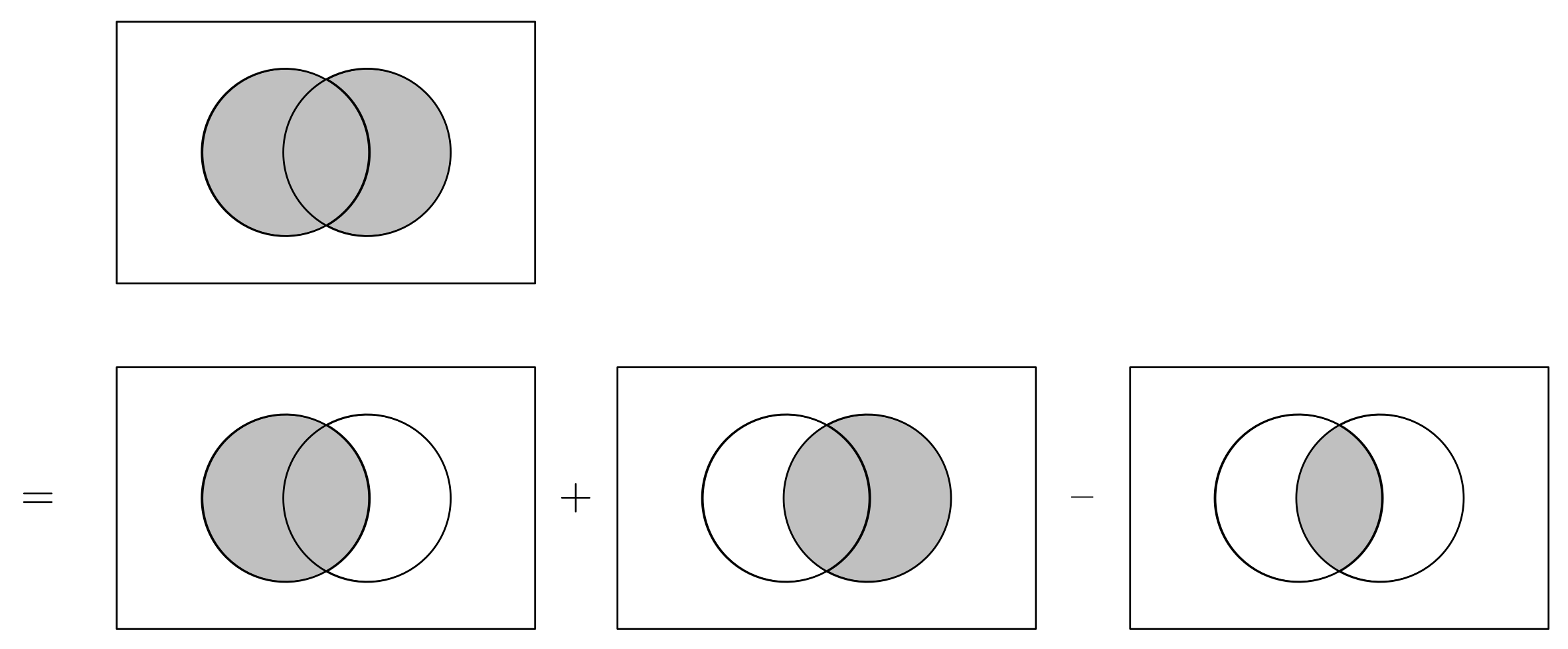
ユーリ「ほほー。にゃるほど。 両方足しておいて、重なったところを引く……そーだね!」
僕「ねえ、ユーリ」
ユーリ「何?」
僕「くどくどと日本語で書くよりも数式の方がずっと短く書けると思わない?」
ユーリ「うーん……短く書けるけど、でもわかりにくいよー」
僕「記号に慣れないといけないからね。 じゃ、問題だよ。正しいものをすべて選ぼう」
問題(集合の要素数)
正しいものをすべて選ぼう。 ただし、集合の要素数はすべて有限個とする。
(1)どんな集合 $A$ に対しても、 $|A| \geqq 0$ が成り立つ。
(2)どんな集合 $A$ と $B$ に対しても、 $|A \cap B| \leqq |A|$ が成り立つ。
(3)どんな集合 $A$ と $B$ に対しても、 $|A \cup B| \geqq |A|$ が成り立つ。
(4)どんな集合 $A$ と $B$ に対しても、 $|A \cup B| \leqq |A| + |B|$ が成り立つ。
ユーリ「……」
ユーリは僕が問題を出したとたん、モードが切りかわった。 急速思考モードだ。口を閉じ、真剣な顔。栗色の髪が金色に輝く。 いつもの軽口を叩いているユーリとはちょっと違う。 僕は黙って、ユーリのモードが再び切り替わるのを待つ。
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2014年1月31日)
この記事は『数学ガールの秘密ノート/場合の数』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!