![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/場合の数』として書籍化されています。
ユーリ「ねーお兄ちゃん、何かおもしろいパズルない?」
僕「何だよ出し抜けに」
いとこのユーリは中学二年生。 僕より三歳年下だ。 ひまがあると僕の部屋に遊びに来る。 いっしょにゲームをしたり、パズルを解いたりして遊ぶこともある。 最近はいっしょに数学をやることも多くなった。
ユーリ「うーん、とある知人にパズルの問題出したくて」
僕「とある知人?」
ユーリ「センサクはいいから、パズル」
僕「そういわれてもなあ」
ユーリ「ほら、いつだっけ《ぐるぐるワン》のパズルいっしょにやったじゃん。 あれおもしろかった」
僕「あの時計パズルはユーリが持ってきたんじゃないか」
ユーリ「そーなんだけど、お兄ちゃんがいろいろ説明してくれたから、 すっごく楽しかった!」
僕「それはよかった」
僕「何いまの」
ユーリ「それはさておき、パズル」
僕「そうだなあ。だいたい、数字を並べていくとおもしろいこと考えたくなるものだよ」
ユーリ「そー?」
僕「たとえば、こんなふうに時計を描いてみよう」

ユーリ「針がなくて時計に見えない」
僕「まずは数字だけ……それで、と」
ユーリ「わくわく」
僕「いや、ユーリも考えるんだよ……」
ユーリ「そんなこと言われても、なに考えていいのかわかんないもん」
僕「何でもいいんだよ。そうだなあ……じゃ、色分けでもしてみようか」

ユーリ「ほほー。えっと……ははーん、左右対称に色分けしたってことだね?」
僕「え! いや、そういうつもりはなかったんだけど、そうなってるな」
ユーリ「へ? じゃあ、どーゆーつもりで色分けしたの?」
僕「倍数ごとに色を変えただけだよ」
ユーリ「ふーん、なるほど。青は $2$ の倍数で、赤は $3$ の倍数で……あれ? でもおかしいよ。 だって、 $6$ は $2$ の倍数なのに青になってない!」
僕「お、ちゃんとチェックしてるなあ。 倍数ごとに色を変えたというのは不正確な言い方だったかな。 こんなふうに色を分けてみたんだ」
ユーリ「うわ、ややこしい……素直じゃない分け方!」
僕「そんなことないよ。ややこしく聞こえるけど、 要するに《$2$ の倍数かどうか》と《$3$ の倍数かどうか》で分けているんだよ。 こう言い換えるともっとすっきりするかな」
ユーリ「余計ややこしくなったかも!」
僕「そんなことないって」
ユーリ「かつってゆーのは?」
僕「『AかつB』っていうのは、『AとBの両方』という意味だよ」
ユーリ「ふーん……」
僕「たとえば、《$2$ の倍数である》かつ《$3$ の倍数である》数っていうのは、 《$2$ の倍数と $3$ の倍数の両方である》数のこと。つまり $6$ の倍数だね」
ユーリ「ほほー」
僕「$1$ 以上 $12$ 以下の整数は、この $4$ 種類のどれかに分類されるね。 もれもないし、だぶりもない」
ユーリ「ふんふん……まーでも、やっぱりややこしーよね」
僕「うん、じゃあね、この $12$ 個の数をこんな風に並べてみよう」
ヴェン図
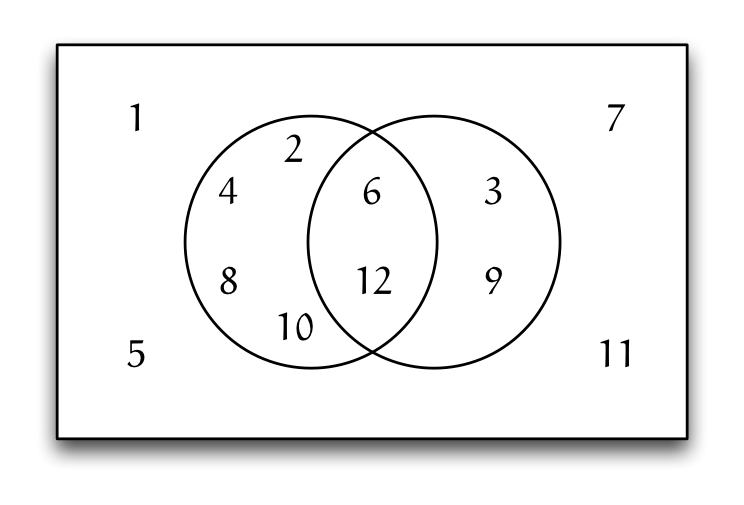
ユーリ「おっと!」
僕「これはヴェン図だね」
ユーリ「べんず……これ、学校で習ったよ」
僕「たくさんのものを集めたときに、 それぞれの集まりがどういう関係にあるかを表している図だ。 集合の包含関係を表す図」
ユーリ「ほーがんかんけー?」
僕「そうそう。包含の『包』は『つつむ』という字で、『含』は『ふくむ』という字だよ。 ある集合が他の集合をどんなふうに含んでいるかという関係が包含関係」
ユーリ「この左側の丸の中は $2$ の倍数でしょ?」
$2$ の倍数

僕「そうだね。 $1$ から $12$ までの整数のうち、 $2$ の倍数を左の円の中に入れて表している。 $2,4,6,8,10,12$ の $6$ 個だね」
ユーリ「そんで、右側の丸は $3$ の倍数だよね?」
$3$ の倍数
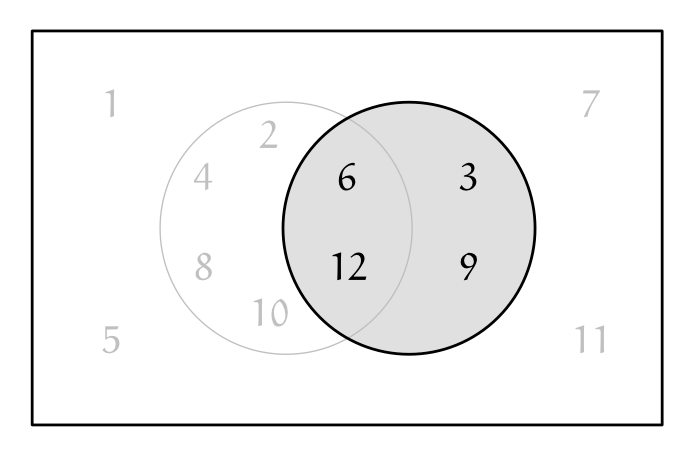
僕「そう。 $3$ の倍数は $3,9,6,12$ の $4$ 個」
ユーリ「真ん中の重なったところが $6$ の倍数!」
$6$ の倍数

僕「その通り。この重なったところを、 二つの集合の共通部分と呼んだり交わりと呼んだりするよ」
$2$ の倍数の集合と、 $3$ の倍数の集合の共通部分(交わり)

ユーリ「アーモンドみたい」
僕「そうだね。でも、ヴェン図では図形の形は気にしないんだ」
ユーリ「ふーん」
僕「そのアーモンド……《$2$ の倍数の集合》と《$3$ の倍数の集合》との共通部分は、 《$2$ の倍数である》かつ《$3$ の倍数である》数の集合ということになるね」
《$2$ の倍数である》かつ《$3$ の倍数である》数の集合

ユーリ「そりゃそーだ。当たり前じゃん」
僕「じゃあ、これはどんな数?」
クイズ(どんな数?)
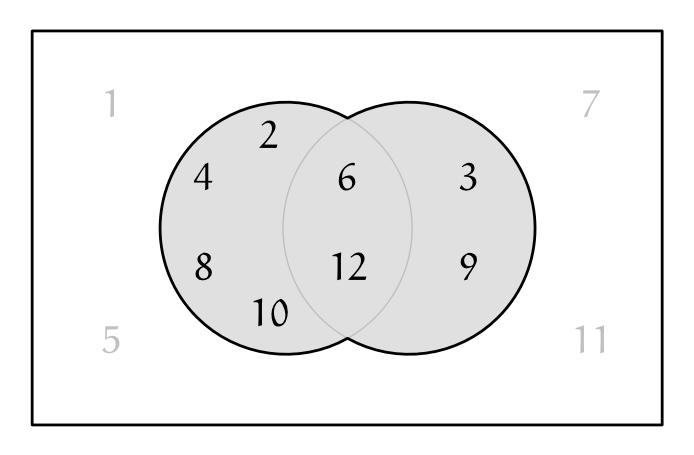
ユーリ「おっ! ……急にクイズ出さないでよ。えーとねー。 $2$ の倍数と $3$ の倍数を合わせたの」
僕「そうだね。これを二つの集合の和集合と呼んだり結びと呼んだりする」
$2$ の倍数の集合と、 $3$ の倍数の集合の和集合(結び)

ユーリ「カンタンカンタン!」
僕「この和集合は、《$2$ の倍数である》または《$3$ の倍数である》数の集合になるよね。 『AまたはB』っていうのは、『少なくともAとBのどちらか片方(両方でもいい)』という意味」
ユーリ「要するにどっちでもいいってことでしょ?」
僕「そうだね」
《$2$ の倍数である》または《$3$ の倍数である》数の集合

ユーリ「ふんふん」
僕「じゃあ、ここでクイズだよ。 これはどんな数の集合?」
クイズ(どんな数の集合?)
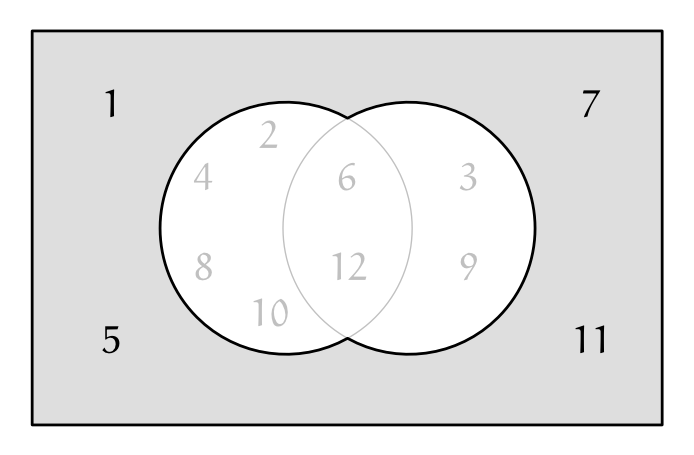
ユーリ「どんな数って……あれでしょ。 《$2$ の倍数でも $3$ の倍数のどっちでもない》数」
僕「そうだね。 言い換えると《$2$ の倍数でない》かつ《$3$ の倍数でない》数の集合になる」
クイズの答え(どんな数の集合?)
《$2$ の倍数でない》かつ《$3$ の倍数でない》数の集合。

僕「ねえ、ユーリ」
ユーリ「なに?」
僕「この二つの図、並べてみるとおもしろくない?」
図a. 《$2$ の倍数である》または《$3$ の倍数である》数

図b. 《$2$ の倍数でない》かつ《$3$ の倍数でない》数

ユーリ「あ! ひっくり返ってる!」
僕「そうだね。図aで色が着いているところは図bでは色が着いていないし、 図aで色が着いていないところは図bでは色が着いている。 ちょうど反対になっている」
ユーリ「そーだね」
僕「これを補集合って呼ぶんだよ。 図aの補集合が図bで、図bの補集合は図a」
ユーリ「ふーん」
僕「じゃ、もう一つ、大きな問題を出そう」
ユーリ「なになに?」
僕「二つの円からなるヴェン図を見てきて、 いろんなパターンがあることがわかった。 $2$ の倍数、 $3$ の倍数、共通部分、和集合……」
ユーリ「ま、そーだね」
僕「いままで見つけたのは、何個あった?」
ユーリ「えーとねー……たぶん $5$ 個くらい?」
僕「ぜんぶでいったい何パターンあると思う?」
問題(ヴェン図)
$2$ 個の円で作られるヴェン図で、 これまでに次の $5$ 個のパターンを見つけた。 ぜんぶで何個のパターンがあるか。





ユーリ「たぶん $8$ 個じゃない?」
僕「おいおい、どうしてそう思ったの」
ユーリ「何となく。偶数になりそうだって思ったから」
僕「いいかげんだなあ……」
ユーリ「わかったよー。描けばいいんでしょ?」
僕「素直だなあ……」
ユーリ「まずね、ユーリ気づいてたことがあるんだ」
僕「というと?」
ユーリ「ほらさっき、お兄ちゃんがほしゅーごーのこと話してたじゃん。 だからね、ひっくり返すパターンが必ずあるの。 でもいままでに見つけたのは $5$ 個で奇数でしょ? だからすぐに見つかる補集合がある」
僕「賢いなあ!」
ユーリ「まず、 $2$ の倍数の集合の補集合」
$2$ の倍数の集合の補集合

僕「うん、これは奇数の集合だね」
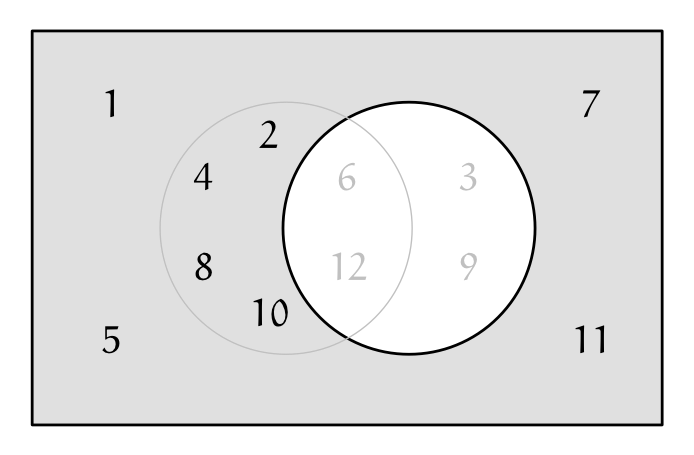
ユーリ「それから、 $3$ の倍数の集合の補集合」
$3$ の倍数の集合の補集合
僕「いいぞ!」
ユーリ「それから、 $6$ の倍数の集合の補集合。へんな形!」
$6$ の倍数の集合の補集合

僕「これで $8$ 個になったな」
ユーリ「ね! だから言ったでしょ? $8$ 個だって」
僕「おいおい。他にはもうないって?」
ユーリ「あるの?」
僕「降参するなら答えを……」
ユーリ「待って! 待ってよー……考えるから」
ユーリは図をじっと見つめて他にパターンがないかを探し始めた。 彼女の栗色の髪が金色に輝く。 考えているとき、僕は静かに待つ。
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2014年1月24日)
この記事は『数学ガールの秘密ノート/場合の数』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!