![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/ベクトルの真実』として書籍化されています。
いつものように僕が図書室に行くと、テトラちゃんがノートに向かって熱心に何か書いている。 どうやら問題を解いているらしい。 彼女は真剣な顔でノートにしばらく書き、やがて手をとめ、大きな目をぱちぱちさせてから頭を抱える。 そしてまたページをめくって書き始める。 しばし僕は、そんな繰り返しを眺めていた。
僕「ねえ、テトラちゃん」
テトラ「あ、先輩!」
僕「一生懸命だね。それは数学?」
テトラ「は、はい……」
僕「村木先生の?」
テトラ「いえ、違います。問題集で」
僕「たくさん書いていたみたいだけど」
テトラ「え、見てらしたんですか! お恥ずかしいです。この問題を解こうとしていたんですけれど、うまくいかなくて」
問題
円 $x^2 + y^2 = 1$ 上の点 $(a,b)$ で、この円に接する直線 $\ell$(エル)の方程式を求めよ。
僕「ははあ、なるほど。これはね」
テトラ「あああああっ! 言わないでください!」
僕「?」
テトラ「答え、言わないでください! いま求めようとしているんですっ!」
僕「はいはい、そうだね。ごめんごめん。それで……どこまで出来たの?」
テトラ「実はですね、何回かチャレンジしているんですが、 毎回、すごく複雑な式になってしまいまして……」
僕「ノート、見せてもらってもいい? 大丈夫。答えは言わないから」
テトラ「は、はい。最初はこう考えたんです……」
テトラちゃんの解きかけ(1)
求める直線 $\ell$ の方程式を $y = cx + d$ とします。
接点 $(a,b)$ はこの直線 $\ell$ の上にありますから、 直線 $\ell$ の方程式 $y = cx + d$ で $x = a, y = b$ とした式が成り立ちます。 $$ b = ca + d \qquad \textbf{(A)} $$
また接点 $(a,b)$ は円の上にもありますから、 円の方程式 $x^2+y^2=1$ で $x = a, y = b$ とした式が成り立ちます。 $$ a^2+b^2 = 1 \qquad \textbf{(B)} $$
(B)の式に対して(A)の $b = ca + d$ を代入します。
$$ a^2 + (ca + d)^2 = 1 $$
展開します。
$$ a^2 + c^2a^2 + 2cad + d^2 = 1 $$
それで?
僕「ノートが『それで?』で終わっているね」
テトラ「は、はい。そこまで書いたところで、こんなに複雑な式が出てきていいのかなと思い始めまして……それで、 もう一度読み返してみると、あたしが書いた一番始めにまちがいを見つけたんです」
僕「まちがい?」
テトラ「はい、あたしは最初に『求める直線 $\ell$ の方程式を $y = cx + d$ とします』と書きましたが、 これだと斜めや水平の直線は表していますけど、垂直の直線は表していないですよね。確か」
テトラちゃんはそういって両手で水平・垂直のジェスチャをする。 まるで忍者が体操しているようだ。
僕「まあそうだね。$y = cx + d$という書き方だと垂直の直線は表せない。垂直の直線は$x = \REMTEXT{定数}$という形だから」
テトラ「はい……ですからあたし、もっと『一般的な直線の方程式』というものを参考書で見て、 次の解き方に挑戦したんです、が」
僕「次のページかな?」
テトラちゃんの解きかけ(2)
求める直線 $\ell$ 上の点を $(x,y)$ とし、 直線 $\ell$ を $x = ct + d, y = et + f$ で表します。 ここで、 $c,d,e,f$ は定数で、 $t$ はパラメータです。
↑注意! ここ、わかってない(><)
この点 $(x,y)$ は円上にありますから、 円の方程式 $x^2 + y^2 = 1$ に $x = ct + d, y = et + f$ を代入して、 次の式を得ます。
$$ (ct + d)^2 + (et + f)^2 = 1 $$
展開します。
$$ c^2t^2 + 2ctd + d^2 + e^2t^2 + 2etf + f^2 = 1 $$
えっと?
僕「ノートが『えっと?』で終わっているね」
テトラ「は、はい……ここまで書いて、さっきの《解きかけ(1)》よりもずっとややこしくなっていることに 気づいたんです。それで頭を抱えてしまって」
僕「そういえば、頭、抱えてたね」
テトラ「それにですね。参考書で見た最初のところの『パラメータ』というあたり、 実はあたしよくわかっていないんです」
僕「なるほど。そういえば途中に『ここ、わかってない』って書いてあったね」
テトラ「はい、でも、こういう直線の表し方があるというので、 それを使えばきれいな式が出てくるのかなと思っていたのですが……どうも、そうではないようです。 あの、あたしって、よくこういうことが起きるんです」
僕「こういうことって?」
テトラ「式がすごく複雑になって、文字がたくさん出てきて、 『ああ、まずいまずいっ! このパターンはまずいっ!』って思うんですけれど、 どうしようもなくなるという」
僕「なるほどね。確かにそういうときはあるよね」
テトラ「なぜなんでしょう。あたしの方法って、どうして行き詰まってしまうんでしょう?」
僕「ねえ、テトラちゃん。答えは言わないから、少し話してもいいかな」
テトラ「は、はい……もちろんです。先ほどは『言わないで!』なんて言ってしまいましたが、 教えていただきたいです」
僕「テトラちゃんの《解きかけ》はそんなに悪くはないんだけど、 とても大きな、まずいことがあるんだ」
テトラ「え! なんですか?」
僕「うん。問題の文章の中に《円》や《接点》や《直線》という図形の言葉がたくさん出てきているよね。 こういうときは何よりも《図を描いて考える》ようにしなくちゃ!」
テトラ「あ! そ、そうですね、確かに!」
僕「図を描いて考える。それはとても大切なことだよ。 確かに図形の方程式が出てきているから、数式を書いたり式変形をしたりすることになるよ。 でも、まずは図を描いて考える。できるだけきれいに図を描くと、 テトラちゃんが見落とした条件も見つかるんじゃないかな」
テトラ「あ、あたし、何か条件を見落としていましたか?」
僕「まずは図を描いてみようよ」
テトラ「そ、そうですね。……こうでしょうか」
テトラちゃんの図
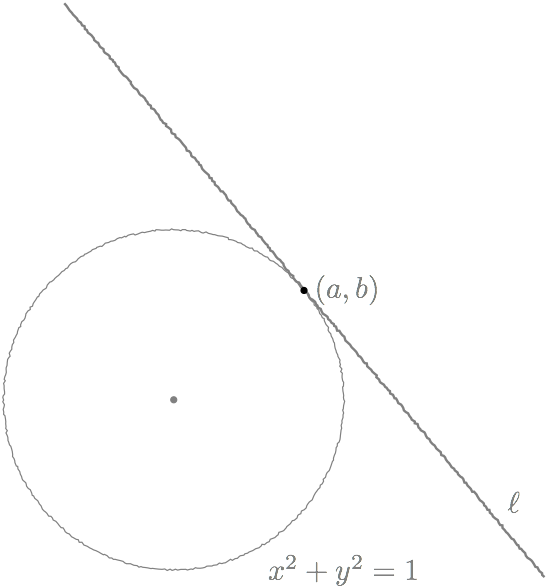
僕「……じゃあ、問題文をゆっくり読んでみて。この図を指さしながらね」
テトラ「はい。《円 $x^2 + y^2 = 1$ ……》で、これが円ですよね」
僕「うん。そうだけど、この方程式から半径はわかるはずだよね?」
テトラ「はい。方程式が $x^2 + y^2 = 1$ ですから半径の二乗が $1$ になるので半径は $1$ です」
僕「だったら、そのことも図に書かなきゃ。半径は $1$ だし、中心は原点 $(0,0)$ だよね。座標軸も描いてみようか」
テトラ「あ! 確かにそうですね……」
僕「問題文の続きを読んでみて」
テトラ「はい。《円 $x^2 + y^2 = 1$ 上の点 $(a,b)$ ……》ですから、ここに点 $(a,b)$ を描きました」
僕「うん」
テトラ「《円 $x^2 + y^2 = 1$ 上の点 $(a,b)$ で、この円に接する直線 $\ell$ の方程式を求めよ》ですから、 点 $(a,b)$ で円に接する直線 $\ell$ です……先輩。ここまでで、あたし、条件を何か見落としてますか?」
僕「そうだね」
テトラ「え! ……わかりません」
僕「テトラちゃんのさっきの《解きかけ(1)》でも《解きかけ(2)》でも、 点 $(a,b)$ が円と直線 $\ell$ の上にあるという条件を使っていたよね」
テトラ「はい」
僕「でも、この直線 $\ell$ が点 $(a,b)$ で円に接しているという条件は使ってなかったよね」
テトラ「ああっ! ……確かにそうですね!」
僕「テトラちゃんがこの問題にチャレンジしているときに使おうとした武器はこれだよ」
テトラ「確かに、そうです……」
僕「でも、円と直線が《接する》という条件をうまく使うと、 もっとずっと簡単に問題を表現できるんだよ」
テトラ「そうなんですか?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2013年12月13日)
この記事は『数学ガールの秘密ノート/ベクトルの真実』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!