第53回 シーズン6 エピソード3

無数の等しい矢（前編）

図書室にて

僕「……ユーリと、そんな話をしてたんだよ」

テトラ「ユーリちゃんってすごいですね。ベクトルのこともわかっているんですか」

僕「わかっているといっても、足し算を教えただけなんだけどね。 矢印で平行四辺形を作るというだけだし」

テトラ「それでもすごいと思います。ベクトルという言葉を聞いても『難しい』っていやがらないんですから……あ、 きっと先輩の教え方が上手なんでしょうね」

僕「そうでもないよ」

テトラ「あたしも以前先輩からベクトルについて教えていただいたとき、 いろんなことがはっきりしましたし」

僕「ああ、そんなこともあったね」

テトラ「はい……ええと、単位ベクトルのお話や、ベクトルを成分で考える話。 点と点を計算する話。それから点を座標平面で回転させる話……（第25回参照）」

僕「うんうん。覚えてるよ」

テトラ「ベクトルといえば、少し気になっていることがあるんです。 質問、いいですか」

僕「もちろん、いいよ。何が気になっているの？」

テトラ「先輩はユーリちゃんにベクトルの和を教えるとき、 平行四辺形の対角線を使って説明なさっていましたよね」

僕「そうだね」

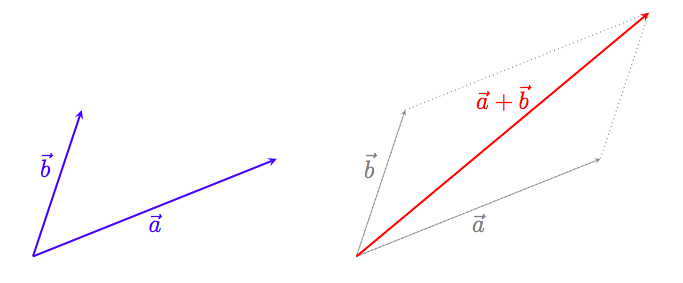
テトラ「確かにこの対角線で何となく足し算をしたという感じはするんですが…… 特に《力》のときにはその感じが強いんですが……あたしはこういう図で納得したんです」

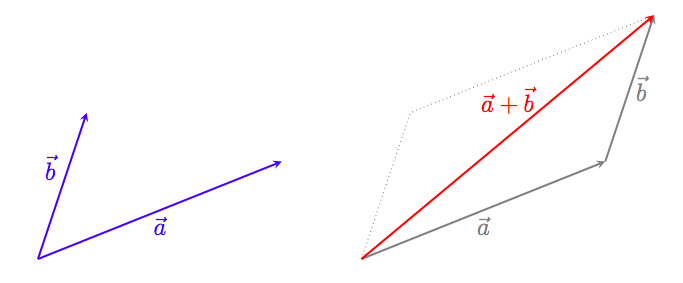
僕「うん、なるほどね」

テトラ「この図だと、 $\vec a$ の始点から終点まで矢印が走っていて、 そしてその終点には $\vec b$ の始点が待っている。そこから $\vec b$ の矢印が走って終点まで行く…… これは本当に $\vec a$ と $\vec b$ を順番に足していってる！　……そんな風に感じたんです」

僕「そうだね。確かにこんな風に終点と始点をつないで考えてもいいよね。 でも、対角線で考えても、つないで考えても、結果のベクトル $\vec a + \vec b$ は等しくなるから、 それでいいんじゃない？」

テトラ「は、はい……それはそうなんですが。 あたし、何にひっかかってるんでしょうね」

僕「何にひっかかっているんだろうね。 たとえば、 $\vec a + \vec b$ と $\vec b + \vec a$ が等しくなる……つまり、 ベクトルの和は交換法則が成り立つこともすぐにわかるよ。何しろ平行四辺形があるからね」

テトラ「はい、それは特にひっかからないです……」

僕「あ、そう」

テトラちゃんは急に黙りこくってしまった。 大きい目をぱちぱちさせながら深く考えている。 僕は黙って彼女が考えをまとめるのを待つ。

彼女は、自分が納得するかどうかにとても関心がある。 テトラちゃんは自分の《わかった感じ》をとても大事にしているのだ。

テトラ「……あのですね、先輩。 あたしがひっかかっているのは、《勝手に動かしていいの？》というところのようです」

僕「勝手に動かす……って、ベクトルを？」

テトラ「はい、そうです。 たとえば、 $\vec a$ と $\vec b$ がこうあるとしますよね」

僕「うん。この二つのベクトルを足そうというんだね」

テトラ「はい。でも、あたしがさっきやった《つなぐ》方法ですと、 $\vec b$ をこんな風にすすすすっと $\vec{b'}$ に動かしてから足さなくちゃいけません」

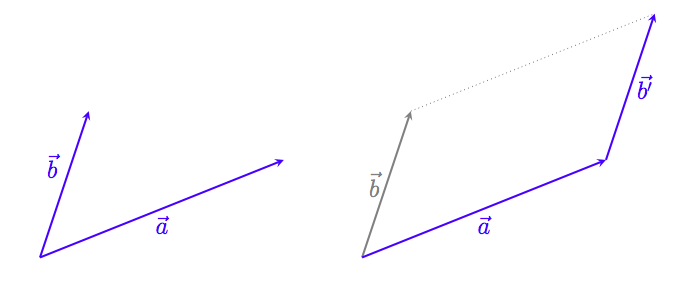
僕「ああ、そういうこと？　それで《勝手に動かす》と……」

テトラ「そうです、そうです。 数を足すときって、勝手に足す数を変えたりしちゃだめですよね。 でもベクトルを足すときには勝手に動かしている……結果はいかにも《足しました》というベクトルに なるんですが、そこにもやもやとした気持ちが残ってしまうんです」

僕「なるほど。つじつまは合っているけれど、勝手に動かしていいのかという疑問だね」

テトラ「はい……なんだか素直に考えられなくてすみません」

僕「いやいや、ぜんぜん謝る必要はないよ！　テトラちゃんの疑問はほんとうに大事な疑問だと思う。 確かにそう感じるのも無理はないよ。足す前に $\vec b$ を動かしているんだから、 それは $\vec{b'}$ のような別の物じゃないかというわけだね」

テトラ「そうですそうです！」

僕「テトラちゃんの疑問には答えられると思うよ」

テトラ「そうですか！　ぜひ教えてください！」