第46回 シーズン5 エピソード6

ディフデフ（後編）

図書室にて

放課後、僕とテトラちゃんはいつものように数学トークをしている。 パスカルの三角形をひとしきり楽しんだ後、テトラちゃんがこんなことを言い出した。

テトラ「先輩のお話を聞くだけじゃなくて、 あたしも、自分の手を動かして考えてみたくなりましたっ！」

僕「うん、それはいいね！　じゃ、僕も村木先生のまねをして、テトラちゃんに《研究課題》を出しておくよ。 数式一つだけ」

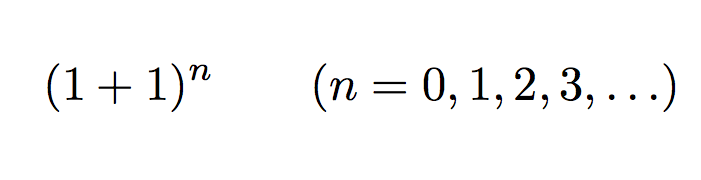
テトラ「これは……」

僕「じゃ、僕はあっちで勉強しているから、また後でね」

テトラ「はい、またのちほど！」

そして時間が過ぎる。

僕が数学の問題を解いていると、 テトラちゃんがそばにやってきて、おずおずと声を掛けてきた。

テトラ「先輩……先ほどの研究課題なんですが」

僕「え？　……ああ、うんうん。何かおもしろいこと、わかった？」

テトラ「これって、あたしが気づいたことへの答えなんですね！」

僕「そうだね。じゃ、話を聞くよ」

テトラ「まず、先輩がくださった式 $(1+1)^n$ を見て、あたしは一瞬『うっ』と思いました」

僕「へえ、どうして」

テトラ「村木先生の研究課題と同じで、『なになにを求めなさい』という問題の形になっていないからです」

僕「ああ、そうだね」

テトラ「それからですね……この $(1+1)^n$ という式には $n$ という文字が入っています」

僕「うん」

テトラ「文字が入るってことは、具体的に計算するのが難しくなります。 なので『うっ』とつまったんです。一瞬」

僕「ふんふん。でも？」

テトラ「はい。でも、落ち着いて考えてみると $(1+1)^n$ というのは、 $(x+y)^n$ で、 $x = y = 1$ としたものと同じでした！」

僕「うん、そうだね。ちょうど公式を復習したところだから」

テトラ「はい。それからあたし、先輩がいつだったかおっしゃってくださったことを思い出しました。 『 $n$ が出てきたら、小さな数で考えてみよう』です」

僕「ああ、それはほんとうに良い方法だよ。それは《例示は理解の試金石》のひとつの例でもあるね。 自分がその式にきちんと向かっているかどうかを確かめるために $n$ に小さな数を入れてみる……」

テトラ「はい、なので、 $(x+y)^n$ を $n = 1,2,3$ でやってみました。そして $x = y = 1$ にするんです」

僕「うん、いいね」

テトラ「それでですね。ここまできてあたしは『あちゃあ……』と思いました。 だって、計算している途中で $1 + 1$ と $1+2+1$ と $1+3+3+1$ とが出てきましたから」

僕「気づいたんだ」

テトラ「はい、気づきました。 $(1+1)^n$ を展開すると、ちょうどパスカルの三角形の行を足した式が出てくるということに！」

僕「そうだね。 $n+1$ 行目の和が出てくる」

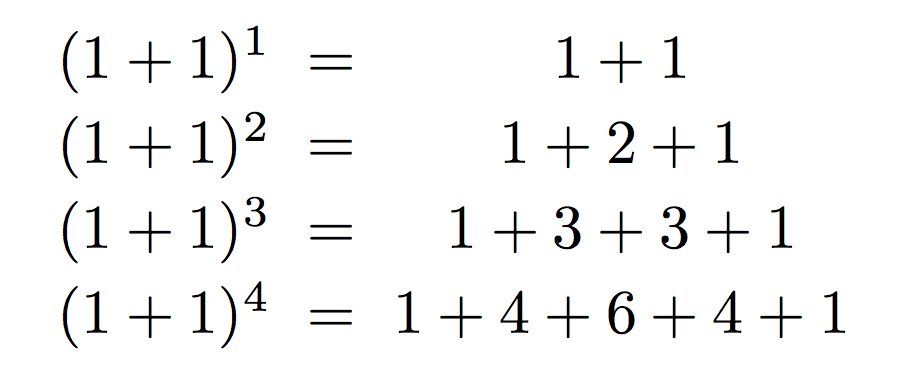
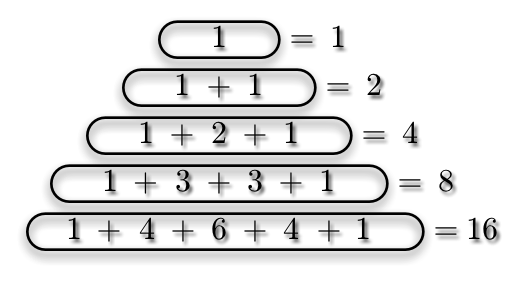
テトラ「考えてみれば当然でした。だって、そもそもパスカルの三角形に出てくる数は、 $(x+y)^n$ を展開したときの係数ですから、 $x = y = 1$ にしてしまえば、パスカルの三角形の行を足した形になるのは当然ですっ！」

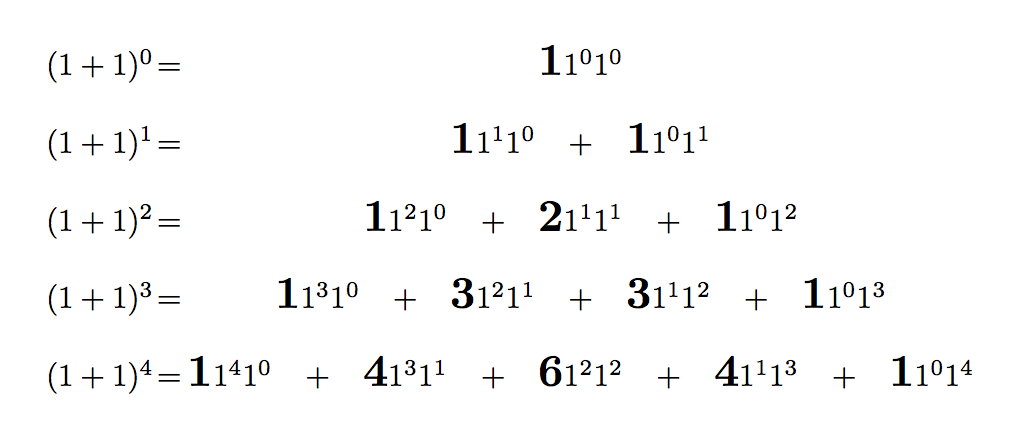
僕「そうだね」

テトラ「それから、 $(1+1)^n = 2^n$ ですから、 結局、パスカルの三角形の行の数を足すと $2$ の冪乗になることがいえるんですね……」

僕「そうそう。さっきはパスカルの三角形に出てくる数が どんなふうに使われてるかを考えて証明したけれど（第45回参照）、 いまテトラちゃんが発見したように $(1+1)^n$ を展開して証明することもできるね」

テトラ「パスカルの三角形って楽しいんですね……組み合わせの数が出てくるし、展開公式とつながるし、 $2$ の冪乗とつながるし……」

僕「だよね。二つの数を加えて次の行の数を作るという簡単なルールなのにね」

テトラ「はい」

二項定理へ

僕「ところでテトラちゃん、さっきは $(1+1)^n$ を $n = 1,2,3$ という具体例で考えたけど、 完全に一般化して、 $(x+y)^n$ を展開した式を書くとこうなるよ。二項定理の式だね」

テトラ「うわ……これは、すごい式……ですね。複雑です」

僕「でも、テトラちゃんはこれを読み解けるはずだよね。 $x = y = 1$ で、 $n = 1,2,3$ の具体例を作れるわけだから」

テトラ「あ、そ、そうですね。すみません、先輩。この $\binom n k$ というのは？」

僕「あ、ごめん。$\binom n k$というのは${}_n\textrm{C}_k$と同じで、《$n$個のものから$k$個のものを取り出す組み合わせの数》だよ」

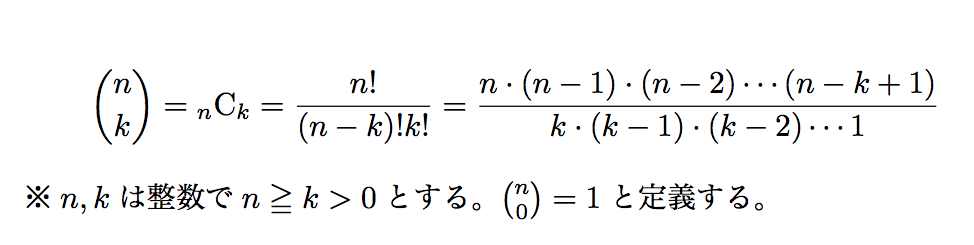
テトラ「そうなんですね」

僕「学校だと${}_n\textrm{C}_k$ばかり使うけど、数学の本を読んでいると$\binom n k$はよく出てくるよ」

テトラちゃんはノートを取り出すとさっとメモを取った。

テトラ「でも、これは複雑ですね！」

微分？

ミルカ「楽しそうだな」

テトラ「あ、ミルカさん！」

ミルカ「今日はなにをやっている？」

テトラ「パスカルの三角形と……それから、二項定理です」

ミルカ「次は微分か」

僕「え、微分？」

ミルカ「テトラに微分を教えていたのではなかったのか」

テトラ「え？」

ミルカ「まあいい」

ミルカさんさんはそういうと、図書室の本棚の方へ行ってしまった。

テトラ「先輩……？　パスカルの三角形のお話が、微分のお話になるんでしょうか」

僕「いや、僕はそのつもりはなかったんだけど……微分？」

テトラ「あれですよね。微分というと、 $nx^{n-1}$ ですね」

テトラちゃんは秘密ノートを開いて言った。

僕「あ、テトラちゃんはもう微分は習ったの？」

テトラ「授業の中で、先生がちらっとおっしゃっていました。あたしはそれをメモしておいただけですが」

僕「なるほど。テトラちゃんはまめにメモを取るからえらいなあ」

テトラ「は……はい。まめメモですねっ！……あたし、何いってるんでしょう」

僕「ところで、テトラちゃんは $nx^{n-1}$ が何を意味しているかわかっている？」

テトラ「はい？」

僕「微分の話の中ででてきたんだよね」

テトラ「はい……ええと、あたしのノートには『$x^n$ を微分すると $nx^{n-1}$』とだけあります」

僕「そうか……」

テトラ「え、ま、まちがってましたか？」

僕「いや、まちがいじゃないんだけど。いろいろ説明は足りないかなと思って」

テトラ「はい、あたし、これはメモしたんですが、実はそれだけで、何もわかっているわけではないです……すみません」

僕「いやいや、それはいいんだけど。 数学で、式や文字が出てくるときには、それが何を表しているかまで確かめる習慣をつけるといいよね」

テトラ「それは、どういうことでしょうか？」

僕「たとえばテトラちゃんは $x^n$ という式を見たとき、何だと思う？」

テトラ「え、 $x^n$ というのは、《$x$ を $n$ 個掛けた式》ではないんですか？」

僕「うん、それでいい。それは完全に正しい。 $x^n$ は《$x$ を $n$ 個掛けた式》だね」

テトラ「……」

僕「それでね、テトラちゃんのメモには、『$x^n$ を微分すると……』ってあったじゃない？」

テトラ「はい」

僕「このときはね、 $x^n$ という式は $x$ についての関数を表しているんだ」

テトラ「は、はい……先輩？　それは《$x$ を $n$ 個掛けた式》とは違うという意味ですか？」

僕「いやいや、そうじゃないよ。 《$x$ を $n$ 個掛けた式》によって表された $x$ についての関数を扱っているということ」

テトラ「……すみません。あたし、先輩がおっしゃっていることがよくわかっていないようです」

僕「そうだね、細かい話と言えば細かい話だし……」

テトラ「でも、何だかとても大切なお話のように思います」

僕「じゃ、ちょっと見方を変えて説明するね。テトラちゃんのメモはこうなっていたよね」

テトラ「はい」

僕「僕がこれに説明を追加すると、こんな感じにしたくなる」

テトラ「……なるほど。少しわかりました。 $x^n$ をぽんとただ書くのじゃなくて、 『これは $x$ についての関数ですよー』ということを意識するということでしょうか」

僕「そうそう！　自分も相手も何を言ってるかよくわかっているなら、『$x^n$ を微分すると $nx^{n-1}$』だけでもいいんだけどね」

テトラ「いえ、教えてくださってありがとうございます。 ……ところで、ここには $n$ が出てきているので、 $n = 1,2,3,4$ で試しに書いてみてもいいでしょうか」

僕「それはいいね！」

微分についてのメモを $n = 1,2,3,4$ について書き直してみる

テトラ「$n$ を具体的に書いてみると、この式にも慣れてきました」

僕「そうだね」

テトラ「これは、あれですよね。《$n$ を下ろして、 $1$ を引く》をすればいいってことですね」

僕「ああ、そうそう。そうだね。 $x^n$ を微分するときには、 指数の $n$ を係数のところに下ろしてきて、指数の $n$ を $n-1$ に変えればいい。 そうすれば $x^n$ から $nx^{n-1}$ が出てくるよね。 そういうふうに考えるのは間違いじゃないよ」

テトラ「あ、先輩……それはいいのですが、考えてみますと、あたしは微分が何かよくわかってないです。 先生がちらっとお話ししたときには、この式の変形を見せてくださっただけで、説明はなかったんです」

僕「そうなんだ。微分っていうのはね、一言で言えば《瞬間の変化率》だよ……あれ？」

テトラ「瞬間の変化率……先輩、どうしました？」

僕「いや、似たような話を最近ユーリにしたなあと思って」

テトラ「ユーリちゃんに……中学生なのに、もう微分をやってるんですか？」

僕「聞かれたから、簡単な話をしただけだよ」

微分の定義

テトラ「……そうなんですね。ユーリちゃんはすごいです。中学生でそんなに理解できるんですか！」

僕「極限の説明は省いたし、時間 $t$ に対する《位置のグラフ》は $p = t^2$ という簡単なものだったしね」

テトラ「それでもすごいです。先輩の教え方が上手なんですねっ！」

僕「あ……そういう意味か」

テトラ「何がですか？」

僕「さっきミルカさんが言ってたことだよ。パスカルの三角形と微分の関係！」

テトラ「はあ……」

僕「パスカルの三角形というよりも、二項定理と微分の関係だよ。なるほど、すっかり忘れていた」

テトラ「どういう関係でしょう」

僕「$x^n$ を微分すると $nx^{n-1}$ になる、っていう話をしたよね」

テトラ「はい。 $n$ を下ろして……」

僕「うん、それそれ。 二項定理がわかっていれば、その $nx^{n-1}$ という式が微分の定義から出てくることがわかるんだよ！」

テトラ「微分の定義……」

僕「そう。ええっとね、僕は中学生のユーリに教えるとき、《位置のグラフ》から《速度のグラフ》を求める方法として、 こんな動点の例を使って教えた」

テトラ「はい。時間 $t$ の $2$ 乗で位置 $p$ が表される動点……ですね」

僕「そうだね。ユーリにはそうはいわなかったけど、この動点は時刻 $t$ が決まれば、位置も決まるよね？」

テトラ「……はい、それはそうですね。時間ごとに位置が定まるということですから」

僕「そのことを数学的に言えば、《この動点の位置は時刻 $t$ の関数である》といえる」

テトラ「ははあ、確かにそうです」

僕「だから、 $p$ と書く代わりに $p(t)$ みたいに表現した方がはっきりするね。位置は時刻の関数だよということが明確になる」

テトラ「あ、あの……その場合でも $p(t) = t^2$ というのは変わらないのですよね？」

僕「うん、そうそう。それで僕はユーリに、時刻が $t$ から $t+h$ に変化したときの速度を計算してみせた。 いや、ユーリが自分で計算したんだったかな」

テトラ「これは、速度が $2t+h$ になったということですか」

僕「そう。そして、『かかった時間 $h$ がとてもとても小さくなったら、速度は $2t$ になるよね』と説明したんだ」

テトラ「とてもとても小さくなったら……ってよくわかりません」

僕「そうだよね。まさにそこが極限の説明を省いたところになる」

テトラ「あ」

僕「でも、速度の式の形 $2t+h$ を考えると、 $h$ が小さいと速度は $2t$ に非常に近くなるというのはわかると思う」

テトラ「それはわかります」

僕「そして、 $2t$ 自体が時刻 $t$ の関数になっているということもわかると思う」

テトラ「それは……時刻の $t$ が具体的に決まれば、 $2t$ も決まるからということで良いですか？」

僕「そうそう。この $2t$ のことを《瞬間の速度》と呼ぶことにすると、ユーリに説明した話は要するにこういうことになる」

テトラ「はい……えっと、あの、それで？」

僕「これが《$x^n$ を微分すると $nx^{n-1}$ になる》の例になっているのがわかる？」

テトラ「……」

僕「だって、 $x$ を $t$ に置き換えて、 $n = 2$ のときを考えてごらんよ、テトラちゃん」

テトラ「え？　《$t^2$ を微分すると $2t^{2-1}$ になる》……ははあ、なるほどですっ！ 《$t^2$ を微分すると $2t$ になる》」

僕「時刻 $t$ の関数として表されている位置を時刻 $t$ で微分してやれば《瞬間の速度》が得られるんだよ。 二つの表現を並べるとこうなる」

• 時刻 $t$ の位置が $t^2$ で定まる動点の《瞬間の速度》は $2t$ になる。
• $t$ の関数 $t^2$ を $t$ で微分すると $2t$ になる。

テトラ「なるほどです。同じですね！」

僕「そして、ここからが二項定理の出番だよ」

テトラ「？」

僕「話が複雑にならないように、ユーリには位置が $t^2$ で表される例を示して微分の話をしたんだけど、 テトラちゃんはもう、 $x^n$ を $x$ で微分する計算ができるよ」

テトラ「え！　そんな、急にいわれましても……」

僕「さっきとまったく同じ計算をすればいいから大丈夫、大丈夫。問題の形にしたらこうなるね」

テトラ「え、あの、答えは $f'(x) = nx^{n-1}$ ですよね？」

僕「そう。それを暗記で答えるのじゃなく、計算で求めてみようということ。計算のとっかかりは、速度のときと同じ」