![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/微分を追いかけて』として書籍化されています。
放課後、僕がいつものように高校の図書室に行くと、 テトラちゃんが《カード》を眺めていた。 例によって村木先生からの数学の問題が出ているらしいな。
僕「テトラちゃん、それは村木先生の新作?」
テトラ「あ、先輩! はい、そうです! あ、でも、新作ですけど、新作ではないです……」
僕「どういうこと?」
テトラ「これなんですが……」
僕「ああ、これは有名なパスカルの三角形だね」
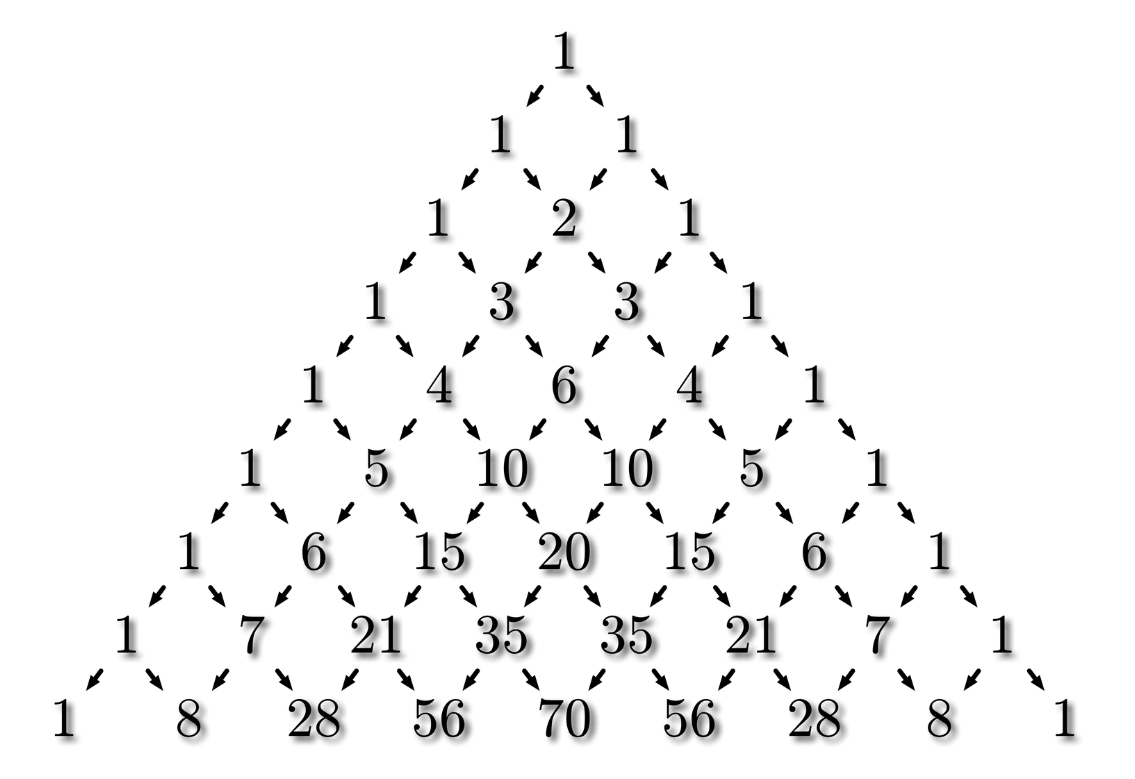
村木先生のカード(パスカルの三角形)

テトラ「そうですね。あたしも知っています。確か……隣り合って並んでいる二つの数を足して下の数を作るんですよね?」

僕「そうだね。パスカルの三角形全体がそうなっている」
テトラ「『なになにを求めよ』みたいに問題の形になってないので、 これは村木先生の《研究課題》ということですよね」
僕「うん。 だから、テトラちゃんの好きなことを自由に考えてレポートにするといいよね。 パスカルの三角形は《研究課題》の定番なんだよ。 この三角形の中にはおもしろい発見がたくさんあるんだ」
テトラ「へ、へえ……二つの数を足して作るだけなのに、 おもしろいものがそんなにたくさん見つかるんですか?」
僕「うん。たとえば、有名な数列がぞくぞく出てくるよ。 まず、単純なものでは、 $1$ 以上の整数 $1,2,3,4,5,6,7,8,\ldots$ がここにあるよね」
$1$ 以上の整数( $1,2,3,4,5,6,7,8,\ldots$ )

テトラ「あ、斜めに見ていくと……そうですね」
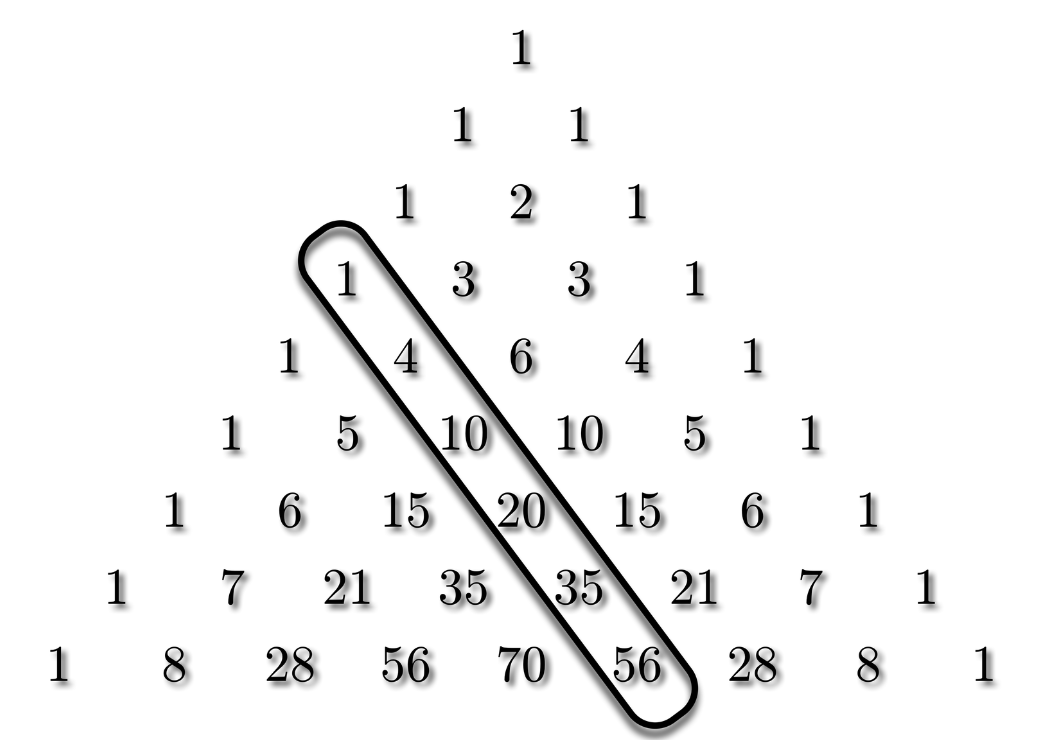
僕「じゃあね、テトラちゃんへクイズだよ。数列 $1,3,6,10,15,21,28,\ldots$ は何かな?」
クイズ: この数列は何?
$$ 1,3,6,10,15,21,28,\ldots $$

テトラ「ええと……何でしょう」
僕「ヒントは三角形だよ」
テトラ「それは、そうですよ。だってパスカルの三角形」
僕「いや、そういうことじゃなくて。これは三角数になる」
テトラ「三角数……というのはどういうものでしたでしょうか、すみません」
僕「ほらほら、こんなふうに三角形の形にものを並べたときの個数だよ」
クイズの答え
$1,3,6,10,15,21,28,\ldots$ は三角数。

テトラ「ああ! これ知ってます!」
僕「そうだね。よく出てくる有名な数列だよ」
テトラ「三角数もパスカルの三角形の中に隠れているんですね」
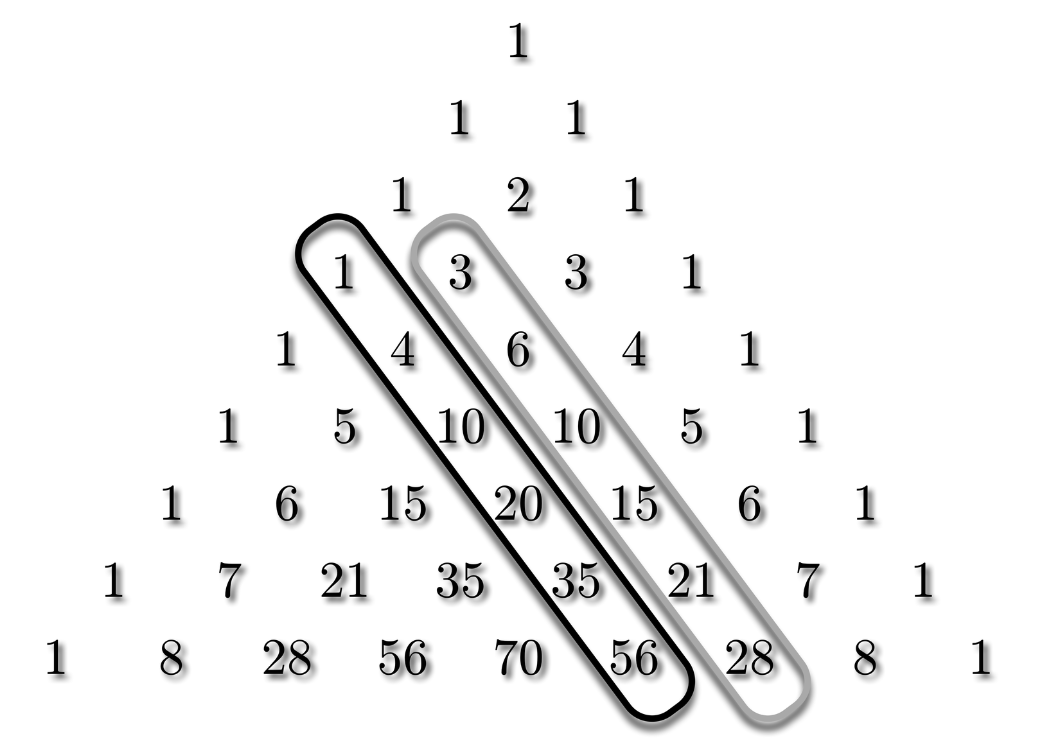
僕「今度は別のクイズだよ。その次の斜めの数列は何になるだろう。 $1,4,10,20,35,56,\ldots$」
クイズ: この数列は何?
$$ 1,4,10,20,35,56,\ldots $$
テトラ「すみません……三角数ですら思い出せなかったので、 この数列はなおさら思い出せません」
僕「いやいや、思い出すのが目的じゃないよ。 思い出すんじゃなくて、考えるんだ」
テトラ「はい……いいえ、あたしも考えたいんですが、 『この数列は何?』といわれても、何をどう考えていけばいいのか……見当もつかないんですが」
僕「いやいや、テトラちゃんは『この数列は何?』と言われたときにわかると思うけど。 数列を調べるときの武器は何だった?」
テトラ「武器ですか? ……あ! もしかして階差数列ですか?」
僕「その通り! 数列が出てきたら、まず階差数列を求めてみる」
テトラ「ではこの数列 $1,4,10,20,35,56,\ldots$ の階差数列を計算すればいいんですね!」
僕「ちょ、ちょっとテトラちゃん!」
ノートに計算を始めようとするテトラちゃんを僕は制する。
テトラ「はい?」
僕「どうして計算するの?」
テトラ「ですから、階差数列を求めるために引き算を順番に……」
僕「パスカルの三角形が目の前にあるのに?」
テトラ「え?」
僕「パスカルの三角形の作り方を思い出してごらんよ」
テトラ「二つの数を足して下の数に……あっ、これって!」
僕「そうそう。そうなんだよ。パスカルの三角形を斜めに見ると、数列の右隣にはその数列の階差数列がある。 計算はしなくてもいいんだよ!」
数列の右隣には階差数列がある
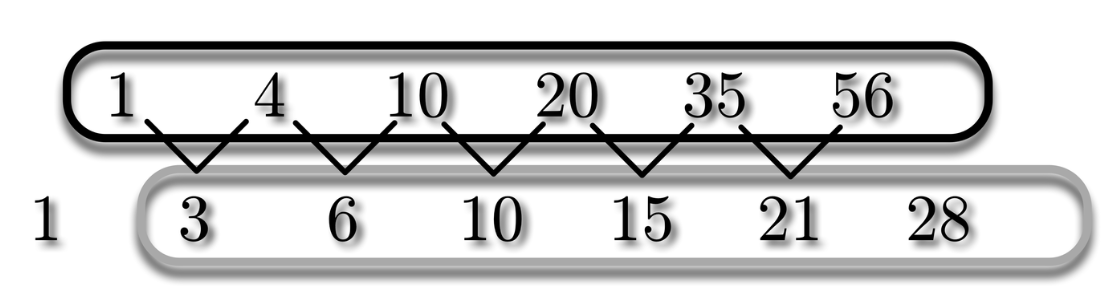
テトラ「なるほど! 確かにそうですね。 ……あたしってびっくりするくらい応用力ないんですね。 パスカルの三角形を足し算で作るってことは知ってるのに、 階差数列に気づかないなんて」
僕「テトラちゃんは自分の手でパスカルの三角形を書いたことはある?」
テトラ「え? 授業で一回書いたことがあるかもしれませんが……」
僕「だよね。僕はよくパスカルの三角形を手で書くよ。 不思議なことに、自分の手を動かしてみると、いろんな発見がある。 斜めの数列の右隣が階差数列になるっていうのは言われてみればあたりまえのことなんだけど、 気がつかない人は気がつかない。でも、自分で書くとそういうところにも気づきやすくなるんだ」
テトラ「そうなんですね……あれ、ところで、数列 $1,4,10,20,35,56,\ldots$ の階差数列が三角数 $3,6,10,15,21,28,\ldots$ だとわかったとして、 結局これで何がいえたことになるんでしょうか? クイズの答えは……」
クイズ: この数列は何? $$ 1,4,10,20,35,56,\ldots $$

僕「うん、これはおもしろいクイズだよ。うんうん。おもしろい」
テトラ「先輩、一人でおもしろがらないでください!」
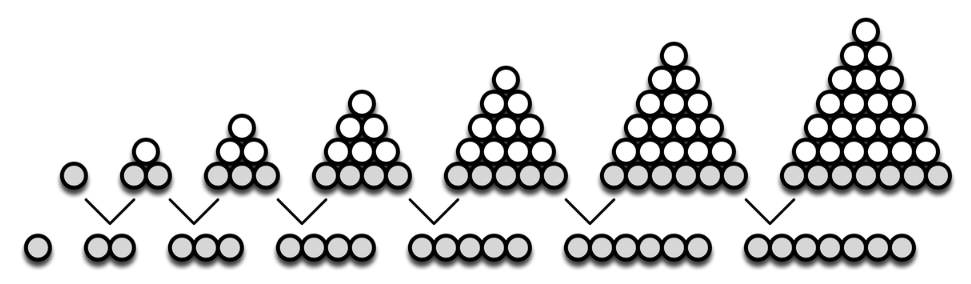
僕「三角数は少しずつ大きな三角形が作られていくよね」
テトラ「はい」
僕「ということは、数列 $1,4,10,20,35,56,\ldots$ は、少しずつ大きくなる三角形を足し合わせて作ったものになってるんだよ」
テトラ「少しずつ大きくなる三角形を足し合わせる……それは、どういうことでしょうか」
僕「三角錐(さんかくすい)だね。 ボールを三角錐……正四面体といったほうがいいかな……の形に積み上げたときのボールの数、 それがこのクイズの答えだよ。 三角錐の高さをだんだん高くしていく。 そのとき、三角錐の底に敷き詰めるボールは少しずつ大きくなる三角形の形になる。 大きくなる三角形を足し込んで作った数は、三角錐数になるんだよ!」
クイズの答え
$1,4,10,20,35,56,\ldots$ は三角錐数。
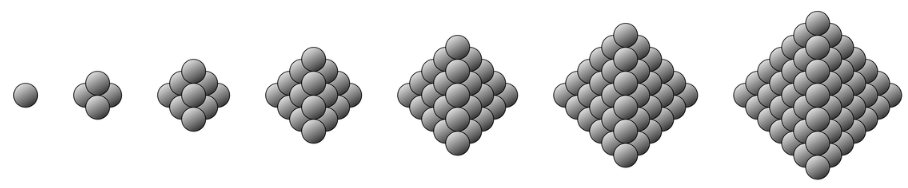
テトラ「なるほど……」
僕「おもしろいよね。三角数のときには階差数列は $2,3,4,5,6,7,\ldots$ で、それはちょうど三角形の底辺を増やす数になってる」
三角数の階差数列は、三角形の底辺を増やす数
テトラ「はあ……」
僕「そして、三角錐数のときには階差数列は $3,6,10,15,21,28,\ldots$ で、それはちょうど三角錐の底面を増やす数になっているんだね!」
三角錐数の階差数列は、三角錐の底面を増やす数

テトラ「なるほどです! おもしろいですねえ……あ! だめですよぅ!」
僕「何が?」
テトラ「だめですよぅ、先輩! このパスカルの三角形はあたしが村木先生からもらったカードなんですから! 先輩がおもしろいものをぞくぞく見つけちゃだめです!」
僕「大丈夫だよ、テトラちゃん。パスカルの三角形の秘密は無数にあるから、いくらでも見つけることができるよ」
テトラ「そうなんですか……」
僕「そうだよ。いままで見てきたのは全部斜めの数列だよね」
テトラ「そうですね」
僕「だったら、今度は水平の数列、つまりパスカルの三角形の各行を考えてみたらいいよ」
テトラ「わかりました! おもしろいこと、あたしも発見します!」
問題: パスカルの三角形の各行のおもしろいことを見つけよう

テトラちゃんは、しばらくノートに向かってあれこれ書き込んでいた。
テトラ「先輩、ちょっと見つけましたよ」
僕「うん、たとえば、どういう《おもしろいこと》?」
テトラ「はい。まずは左右対称だってことです。 ほら、どの行も左右対称になりますよね。 $1, 3, 3, 1$ や $1, 4, 6, 4, 1$ とか」
僕「うん、いいね。それは確かにパスカルの三角形の重要な性質だ」
テトラ「それからですね、さっき先輩は数列でお考えになりましたよね。 ですから、あたしは数の列を見るのではなくて、計算をしてみました。行の数をぜんぶ足すんです!」
僕「ふむふむ」
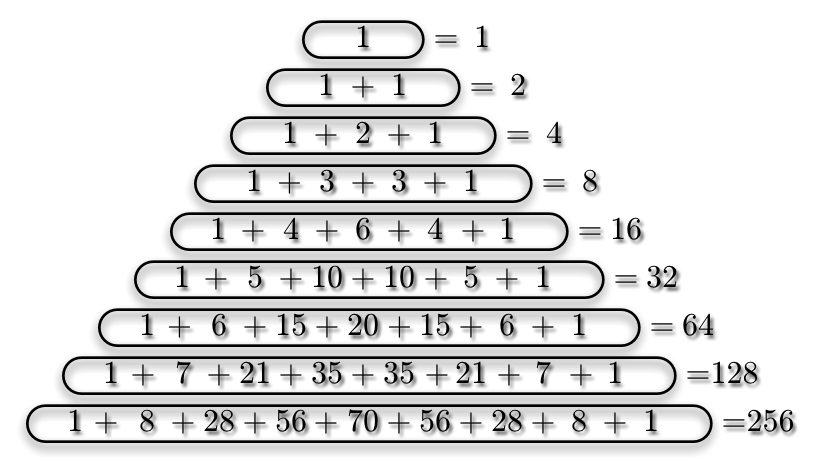
テトラ「するとですね、これはすごいです。どの行も $2$ の冪乗になるんですよ。 $1$ に、 $2$ に、 $4=2^2$ に、 $8=2^3$ に、 $16=2^4$ 、に $32=2^5$ に……」
行の和は $2$ の冪乗になる
僕「いいね! でもテトラちゃん、いま言った『数の列を見るんじゃなくて』っていうのはどういう意味?」
テトラ「はい?」
僕「ほら、『数の列を見るんじゃなくて計算をしてみました』っていったよね」
テトラ「え、はい。ですから、たとえば $1,3,3,1$ という数の列じゃなくて、 全部足して一つの数にしてしまったということです。 $1+3+3+1=8$ で、 $2$ の $3$ 乗ですよね」
僕「うん、計算はそれでいいし、どの行も数を加えたら $2$ の冪乗になるっていうのはとてもいい発見だと思うよ。 でも、テトラちゃんのその計算で《新しい数列》が生まれているよね?」
テトラ「新しい数列といいますと……」
僕「上の行から順番に見ていけば、 $1,2,4,8,16,32,\ldots$ という数列だよ」
テトラ「あ、そういえばそうなりますね」
僕「ところで、証明はできる?」
テトラ「はい?」
僕「せっかくテトラちゃんが見つけた発見だから、証明もしようよ」
問題
パスカルの三角形で、上から $n$ 行目($n = 1, 2, 3, \ldots$)の数をすべて加えたとき、 その和を $a_n$ と書くことにする。このとき、 $$ a_n = 2^{n-1} $$ が成り立つことを証明せよ。
テトラ「え? $a_n = 2^{n-1}$ なんですか? $a_n = 2^n$ じゃなくて」
僕「違うよ。ほら $n = 1$ のときを考えてごらんよ。 $1$ 行目だから和は $1$ だよね。 $a_1 = 2^1 = 2$ じゃなくて、 $a_1 = 2^0 = 1$ にしなくちゃ。 だから、 $a_n$ は $2^n$ じゃなくて $2^{n-1}$ になるよね」
テトラ「あちゃっ! そうですね……」
僕「もっとも、一番上の行を $0$ 行と定義すればそろえられるけど……まあいまは一番上が $1$ 行目だとして、 $a_n = 2^{n-1}$ になることは証明できる?」
テトラ「これは……あの、例の公式を使うんでしょうか」
僕「例の公式って?」
テトラ「あの、《$n$ 個のものから $k$ 個取り出したときの組み合わせの数》です。 ${}_n{\rm C}_k$ です。パスカルの三角形を習ったときに出てきた記憶があります」
僕「ああ、確かにその方法もいいけど、パスカルの三角形の作り方から考えるとすぐにわかるよ」
テトラ「すぐに?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2013年9月6日)
この記事は『数学ガールの秘密ノート/微分を追いかけて』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!