第41回 シーズン5 エピソード1

18歳未満の論理学（前編） ただいま無料

図書室にて

僕「テトラちゃん？」

テトラ「……」

僕「テトラ……ちゃん？」

テトラ「……」

僕「……テトラちゃん、もしかして、眠ってる？」

テトラ「……！」

テトラちゃんが急に顔を上げたので、あやうくテトラちゃんの頭突きでアッパーカットをくらうところだった。 あぶないあぶない。

僕「寝てたんだね」

テトラ「はっ！　せ、先輩……お恥ずかしいです」

僕「数学やっているうちに寝ちゃったの？」

テトラ「はい、いいえ、数学というか……村木先生からいただいたカードを見てただけなんですが、いつのまにかウトウトっと」

僕「村木先生のカード？」

テトラ「これです」

《以上》の定義

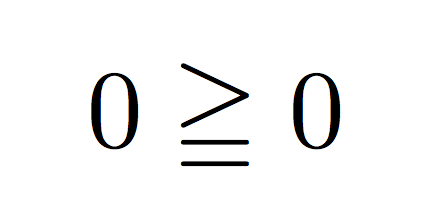
僕「これはまた……簡単というか、単純というか」

テトラ「はい」

僕「例によって《研究課題》……なんだろうけど、こんなに簡単な式は珍しいな」

テトラ「そ、そうですね……あたし、この数式見ているうちに、ぜんぜん違うこと考えていました」

僕「ぜんぜん違うこと？」

テトラ「はい、この $0\geqq0$ をじっと見てたら、人の顔に見えてきたんです」

僕「人の顔に見える……かなあ」

テトラ「はい、 $0$ が目で、 $>$ が鼻で、 $=$ が口で……」

僕「あはは……確かに。見えるね」

テトラ「そんなことを考えていたらいつのまにか寝ちゃってました……」

僕「そうなんだ」

テトラ「でも、ほんとに、この $0 \geqq 0$ で何を考えればいいんでしょう」

僕「そうだねえ……あ、基本的なことを聞くけど、テトラちゃんはこの式が成り立つと思う？」

テトラ「え？」

僕「この村木先生のカードの数式だよ。 $0 \geqq 0$ は成り立つと思う？」

テトラ「え、ええと……はい、成り立つ、と、思います」

僕「え、成り立つの？」

テトラ「あちゃちゃ！　やっぱりまちがいでしたか！」

僕「え、成り立たないの？」

テトラ「ええっ？」

僕「どっち？」

テトラ「はい、あの、えっと……あたしは、たぶん $0 \geqq 0$ が成り立つ！　と思うのですが、自信はないです」

僕「それは困った」

テトラ「はい……すみません」

僕「いや、謝ることはないよ。ただ、テトラちゃんが何を考えたか、教えてくれる？　 $0 \geqq 0$ という数式を見たときに」

テトラ「はい。あのですね、《$0 \geqq 0$ が成り立つか》は《$0$ は $0$ 以上か》と聞いているわけですよね」

僕「うん、そうだね」

テトラ「ええとですね、《以上》というと、何というか、どうしても《大きい》っていうイメージがあるんです。 でも、 $0$ と $0$ とは等しいですよね」

僕「うん、そうだね。 $0$ と $0$ とは等しいよ」

テトラ「ですから、《$0$ は $0$ 以上である》と言い切っていいのかな、と思ってしまうんです」

僕「なるほど。そうだね、テトラちゃんが言うように《なになにである》と言い切るのは勇気がいるよね」

テトラ「はい、そうです……自信が必要です」

僕「結論からいうとね、 $0 \geqq 0$ は成り立つんだよ。つまり、《$0$ は $0$ 以上である》と言い切っていい」

テトラ「そうなんですか……」

テトラちゃんはいつも使っている《秘密ノート》を開いてメモをする。 彼女は数学で学んだことをまめに書き留めておく習慣があるのだ。

僕「あ、もしも $0 \geqq 0$ が成り立つということをメモしたなら、以上の定義も書いておくといいよ」

テトラ「定義……《以上》に定義なんてあるんですか？」

僕「うん、あるよ」

テトラ「ははあ……」

僕「もちろんこの《以上》の定義の前提として《より大きい》や《等しい》は定義済みでなくちゃいけないけどね。 数式を使った方がわかりやすいかな」

テトラ「これが《以上》の定義なんですか」

僕「そうだね。 $>$ と $=$ が定義されているとして、 $\geqq$ を定義したといえるよ」

テトラ「そうですか。 $x > y$ または $x = y$ ……あの、この《または》というのは？」

僕「うん。《$x > y$ または $x = y$》というのは、 $x > y$ と $x = y$ のうち、少なくとも片方が成り立つということだよ。 もちろん両方が成り立ってもいい。 もっとも $x > y$ と $x = y$ の場合には両方が成り立つことはないけど」

テトラ「せっかく教えていただいたのにすみませんが、これで《以上》が定義されているというのが、まだピンと来ません」

僕「あ、そう？　テトラちゃんはさっき『以上というと大きいってイメージがある』って言ってたじゃない？」

テトラ「はい、そうです。だから $0 \geqq 0$ が成り立つと言い切っていいのか不安で……」

僕「それはね、テトラちゃんが $\geqq$ の定義に戻って考えないからなんだ」

テトラ「定義に戻って考える……といいますと？」

定義に戻って考える

僕「うん、数学では《定義に戻って考える》ということがよくある。《定義に戻って考える》というときもあるし、 《定義に従って考える》というときもある。数学はとても微妙な問題を厳密に取り扱う場合があるから、 《その言葉の定義は何か？》と確かめたり、《定義に戻って考えよう》とするときがよくあるんだ」

テトラ「はい……」

僕「別の言い方をするよ。 僕は、テトラちゃんが《イメージ》や《感じがする》と言ってたのが気になったんだ。 《$x$ は $y$ 以上である》といったときに $x$ の方が大きい《イメージ》がある。その気持ちはわかるけれど、 それは言葉に引きずられているんだね」

テトラ「言葉に引きずられている……確かにそうかもしれません」

僕「それで、村木先生のカードに戻るんだけど、 $0 \geqq 0$ という式は、 $\geqq$ の定義にあてはめてみると、こうなるよね」

テトラ「定義にあてはめる……ははあ、《以上》の定義の $x$ と $y$ に $0$ をあてはめたんですね！」

僕「そうそう。これで、定義に戻って考えているわけだ」

テトラ「は、はい……あの……それで……」

僕「僕たちはいま《$0 \geqq 0$》が成り立つかどうかを知りたい。 定義に戻って考えると、それは《$0 > 0$ または $0 = 0$》が成り立つかどうかを調べればいい」

テトラ「はい、そうですね」

僕「《$0 > 0$ または $0 = 0$》を考えるとき、そこにはもう《$0 \geqq 0$》という式は出てこない。 定義に戻って考えるとそうなるんだ。僕たちは $0 > 0$ と $0 = 0$ を吟味すればいい」

テトラ「……なるほどです」

僕「テトラちゃん！」

テトラ「はい！」

僕「いや、《気をつけ》はしなくていいんだけど……ここで、テトラちゃんに質問です。 $0 > 0$ は成り立ちますか？」

テトラ「いいえ、成り立ちません」

僕「では、テトラちゃんに質問です。 $0 = 0$ は成り立ちますか？」

テトラ「はい、成り立ちます」

僕「《$0 > 0$ または $0 = 0$》に出てくる二つの式のうち、 $0 > 0$ は成り立たないけど、 $0 = 0$ は成り立つ。 ということは $0 > 0$ と $0 = 0$ のうち、少なくとも片方は成り立っているといえますか？」

テトラ「あっ……はい、いえます」

僕「ということは、 $\geqq$ の定義により、 $0 \geqq 0$ が成り立っているといえるわけだね！」

テトラ「なるほどです！　なるほど……そういうふうに考えていくのですね！」

僕「めんどうだけど、やってることは機械的だよね。定義をきちんと押さえて、 定義に具体的な内容を当てはめて、一歩一歩確かめる。これが《定義に戻って考える》というやり方」

テトラ「いえ、めんどうだとは思いません。 そんなふうに一歩一歩進めるというのはとても気持ちのいいことだと思います」

（もしもこれが）と僕は思った。 （もしもこれがユーリだったなら、嵐のように《めんどーい！》とか言いそうだなあ……）

僕「うん、だからね。どうも自信がないなあ、はっきりと言い切れないなあと思ったときは、 考えようとしている数学用語の《定義》を再確認するといいんだよ。これが……」

テトラ「《定義に戻って考える》ですねっ！」

僕「その通り！」

僕とテトラちゃんは微笑み合った。

以下と未満

テトラ「えっと、だから結局、 $0 \geqq 0$ は成り立ちますね。はい、今度はちゃんと《言い切れる》ようになりましたっ！」

僕「そうだね。 $0 \geqq 0$ はいつでも真（しん）になる」

テトラ「《$0 \geqq 0$ が真になる》というのは《$0 \geqq 0$ が成り立つ》と同じですか」

僕「うん、そうだよ。成り立つ、真である……いろんな言い方をするね。正しい、というときもあるかも」

テトラ「言葉は難しいですね」

僕「そうだね。慣れないとどうしてもね。あ、そうだ。テトラちゃんは、《以上》と《より大きい》の違いはわかっている？」

テトラ「あ、はい……その違いはわかっていると思います。 《以上》はその数も含んでいて……あ！　わかりました！」

僕「え、何が？」

テトラ「先輩が教えてくださった《以上》の定義の話です！　あたし、《以上》のこと知ってたんです。 《$x$ が $0$ 以上》というのは $x = 0$ も含むってことです」

僕「……うん、そうだけど」

テトラ「でも、あたし、村木先生の $0 \geqq 0$ が成り立つ！と言い切れませんでした。 あたし、きっちり理解してなかったんですね……でも、もうわかりました」

僕「へえ」

テトラ「はい、こういうことなんですね」

• 《$x$ は $y$ 以上》というのは、 $x = y$ を入れる。
• 《$x$ は $y$ より大きい》というのは、 $x = y$ を入れない。

僕「そうだね」

テトラ「《$x$ は $y$ 以上》というのは《$x \geqq y$》のことで、これは《$x > y$ または $x = y$》です」

僕「うん」

テトラ「そして《$x$ は $y$ より大きい》というのは《$x > y$》のことで、これはさっきの《$x > y$ または $x = y$》の後ろを消したものなんですね」

僕「うんうん、いいまとめだね」

テトラ「……」

僕「それから、不等号の向きが逆になったのが《以下》と《より小さい》。《より小さい》は《未満》ともいう」

テトラ「はい……」

僕「テトラちゃん、何か考えてる？」

テトラ「あ、はい、すみません。ちょっと話が戻っちゃうんですが、英語で《$x$ は $y$ 以上》というとき、 " $x$ is greater than or equal to $y$ ." という表現になるのを思い出したんです」

僕「ああ、なるほど」

テトラ「しかもその《"greater than" or "equal to"》というのは、ちょうど《$x > y$ または $x = y$》と同じ形をしている……って」

僕「うんうん、テトラちゃんの言うとおりだね」

条件を書く

テトラ「あの……先輩。ちょっと気になることがあるんですが」

僕「何？」

テトラ「とても細かいことなんですけれど」

僕「何でもいいよ」

テトラ「先ほど先輩は『$0 \geqq 0$ はいつでも真になる』っておっしゃいましたよね」

僕「え？　ああ、うん」

テトラ「どうしていつでもとおっしゃったんですか。ちょっとひっかかって……」

僕「うん、そんなに深い意味があっていったわけじゃないんだけどね。 たとえば、こんな式を考えてみよう」

$$ x \geqq 0 $$

テトラ「エックスは $0$ 以上……ですか」

僕「うん、そう。 $x \geqq 0$ という式があったとき、 この式は、 $x$ の値（あたい）によって、成り立ったり成り立たなかったりするよね」

テトラ「はい、それはそうですね」

僕「でも、 $0 \geqq 0$ には $x$ みたいな文字は出てこないから、成り立ったり成り立たなかったりすることはないわけだ」

テトラ「ははあ……それで？」

僕「うん。だから、つい『$0 \geqq 0$ はいつでも真になる』っていったんだと思うよ」

テトラ「わかりました！」

僕「納得した？」

テトラ「はい、納得です！　ああ、すっきりしました」

僕「数式に慣れている人は《$x$ は $0$ 以上である》という言葉と、 《$x \geqq 0$》という数式を自由に行き来して考えるけど、 数式に慣れてない人はその行き来ができなかったり、時間がかかったりするかもね」

テトラ「まさにあたしがそれですっ！　その《行き来》に時間がかかったり、 《行き来》の途中で不安になることがあります。 あ、それって先ほど先輩がおっしゃった《定義に戻って考える》のが苦手ということかもしれませんね」

僕「特別の数との大小については別の言い方をすることもあるよね。 たとえば《$x$ は正（せい）である》というのは《$x$ は $0$ より大きい》つまり《$x > 0$》ということだし、 《$x$ は負（ふ）である》というのは《$x$ は $0$ より小さい》つまり《$x < 0$》ということだし」

テトラ「はいはいはい。正である、負である、よく出てきます。あ、では《$x$ は負である》というのは《$x$ は $0$ 未満である》といってもいいですか」

僕「そうそう、そうなるね」

テトラ「《$x$ は負である》というのは $x$ がマイナスのことですよね」

僕「そうだね。 $-1$ や $-3$ のようにマイナスの数の場合に、 $x < 0$ は成り立つし……うん、じゃあ、こんなクイズはどう？」

テトラ「……？」

僕「実数 $x$ を $2$ 乗したら正の数になったということは、 $x^2 > 0$ ということだよね。これが成り立つかどうかは $x$ という文字が具体的に何であるかによる。 そのことは、 $x$ の値に《依存する》と表現することもある」

テトラ「依存する……"depend on"ですね！」

僕「うんうん、そうそう。 で、このクイズは、 $x^2 > 0$ が成り立つなら、実数 $x$ についてどんなことが言えるかなと聞いているんだよ。 もちろん言えることはたくさんあるけど……」

テトラ「あれれ、でも……」

僕「ん？　何かおかしい？」

テトラ「いえ、あの、これ、引っかけクイズですか？」

僕「いやいや」

テトラ「だって、実数だったら二乗したら必ずプラスになりますよね？　だから、 $x^2 > 0$ は《いつでも》成り立つのでは？」

僕「引っかけクイズのつもりはなかったんだけどな……いつでも成り立つわけじゃないよ」

テトラ「え？　……ああああっ！　 $x = 0$ のときがありましたっ！　 $x = 0$ のときは、 $x^2 > 0$ にはなりません！」

僕「そうそう」

テトラ「ということは $x \neq 0$ ですね！」

僕「はい、それで正解だね」

テトラ「$x^2 > 0$ が成り立たないのは $x = 0$ のときだけですね……」

僕「そうだね。その一点だけだよ。 $x$ が実数とすると、 $x^2 > 0$ が成り立つのは $x \neq 0$ のとき。 言い換えると《$x < 0$ または $x > 0$ のとき》ともいえる」

テトラ「はい……でも、あたし、こういう条件めいた話は苦手です……」

テトラちゃんは頭を抱えてうめいた。

数直線

僕「慣れてくれば $>, <, \geqq, \leqq$ のような不等号だけでもわかるけど、 それでも、やっぱりうっかりミスをすることはあるよ」

テトラ「え、先輩も《うっかりミス》なんてするんですか」

僕「そりゃもちろんそうだよ。しょっちゅうまちがう。等号を見落としたり、不等号を逆に考えたりね」

テトラ「あたし、そんなのばっかりです。それどころか、条件をごっそり忘れることもあります。 《条件忘れのテトラ》です……」

僕「できるだけミスを減らすためには、数直線（すうちょくせん）を描くくせをつけるといいよね」

テトラ「数直線……」

僕「うん。実数についての範囲を考えるとき、数直線をさっと描いて、その図を見ながら考えるとまちがえにくいよ。 僕がテストでまちがうのは頭の中だけでぱぱっと考えたときだね。そういうときにうっかりミスをする。 めんどうだったり、このくらいはかんたんだと思ったり……そういうとき」

テトラ「そうなんですね！」

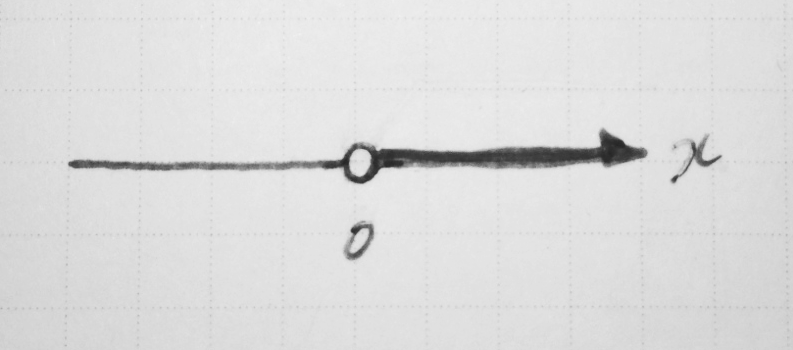
僕「たとえば、 $x \geqq 0$ という条件は、数直線の上にこんなふうに描ける」

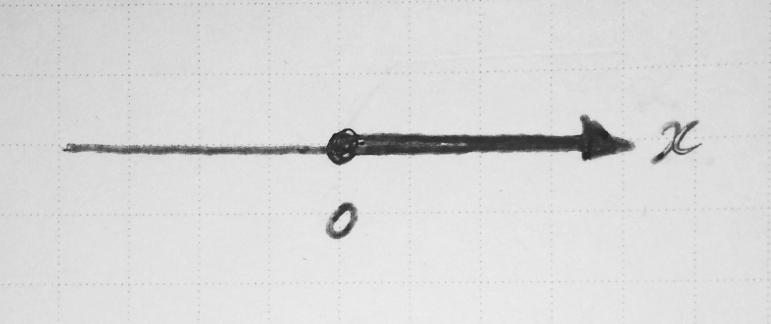
テトラ「そうですね」

僕「太さでわかりにくいときには上に線を引いて範囲がわかりやすいようにすることもある」

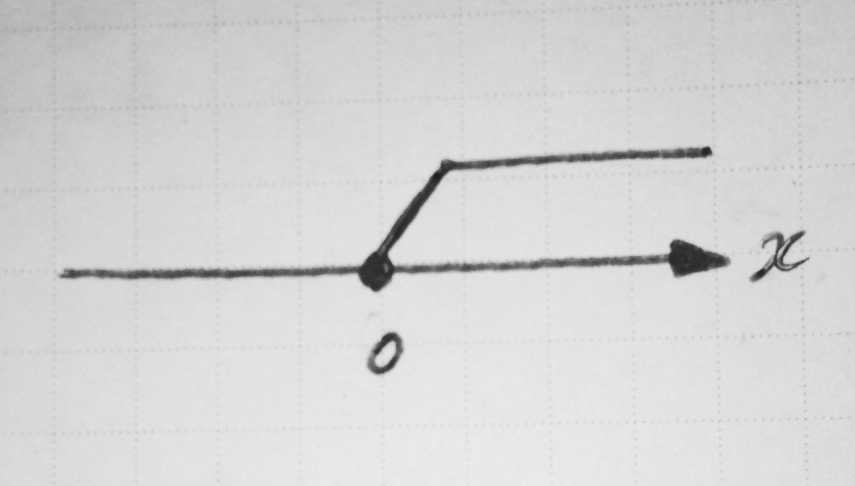
テトラ「はい」

僕「この黒丸の部分は《その点も含む》ということをはっきりとアピールしている」

テトラ「そうですね。……あっ！　わかりました。等号が入るかどうかということですねっ！」

僕「そうそう。もしも、等号が入らない場合には白丸にするね」

テトラ「等号が入らないということは、 $x > 0$ ということですね」

僕「そうそう」

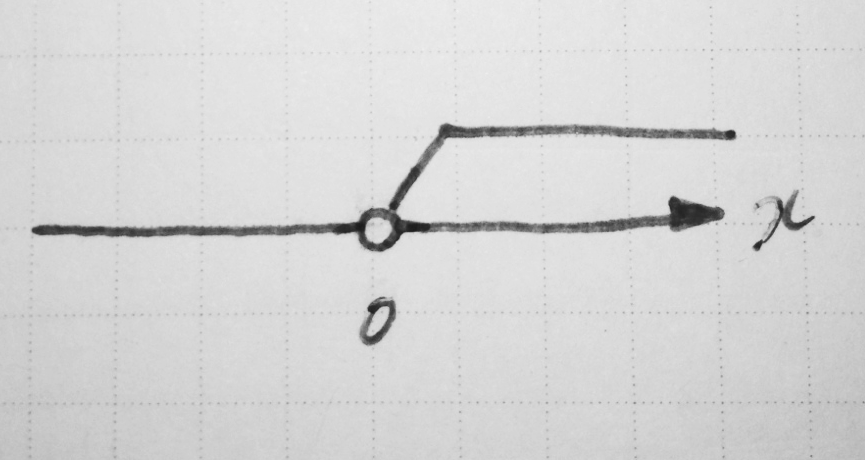
テトラ「はい、わかります」

僕「複雑な条件でも、数直線を使うと考えやすい。たとえば、こんな問題」

テトラ「はわわ……これは描かないと難しいです！」

僕「そうだよね。数式だけでもできなくはないけど、うっかりミスがこわい」

テトラ「ええと……」

だいぶ時間はかかったけれど、 テトラちゃんは焦らずていねいに考えて描くことができた。

テトラ「……こう、ですね！」

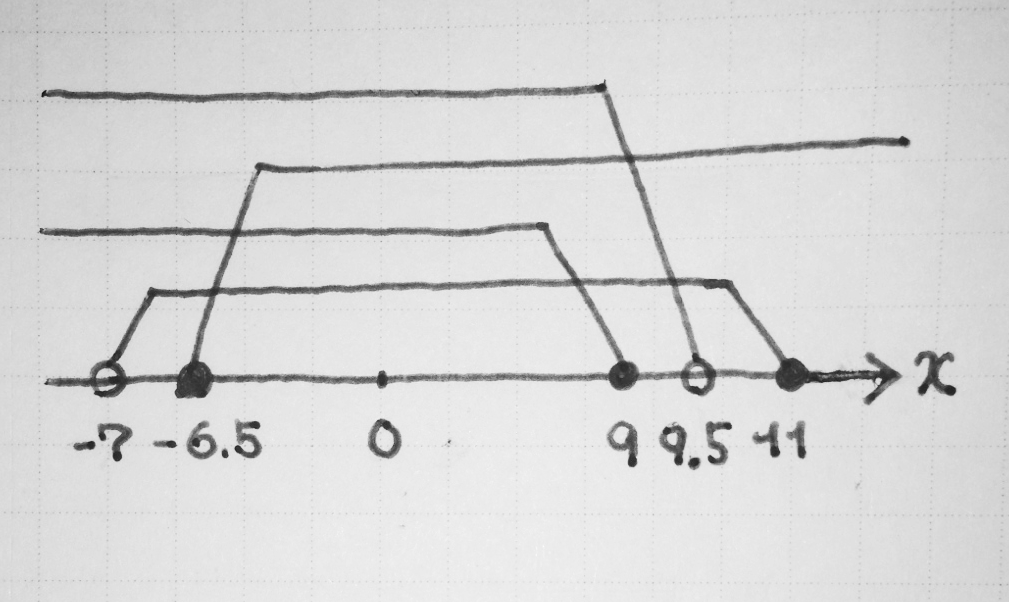
僕「うん、いいね！」

テトラ「それで、《すべて成り立たせる》んですから、全部の重なった部分を考えるんですよね」

僕「そうそう」

テトラ「こうですっ！」

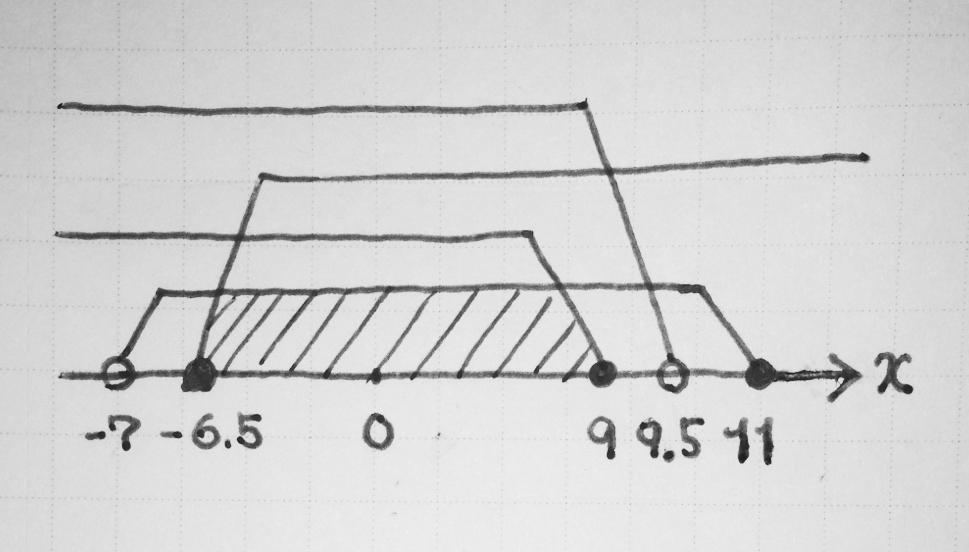
僕「はい、よくできました！　それで答えが出る」

テトラ「はい」

テトラ「頭の中で考えていると、とてもごちゃごちゃするのですが、 ひとつひとつを数直線の上に書いていくと考えやすいです」

僕「そうだよね。ところで、こんなふうに《数直線の上に線を描いて考える》というのは、《実数の集合を考える》ということなんだよ」

テトラ「実数の集合……ですか」

僕「そう。数学の本を読んでいると、よく集合が出てくる。 $x \geqq 0$ という条件を考えるときに、 $x \geqq 0$ という条件を成り立たせるような実数 $x$ をぜんぶ集めたものを考える……集合の考え方だ」

テトラ「ははあ……」

僕「実数をひとつ選ぶと、それは数直線上の一点になる」

テトラ「たとえばそれは $0$ とか……ですか」

僕「うん、そう。 $0$ や $-7$ や $11$ や $-6.5$ や……なんでもいいよ。 $3.14159\cdots$ の $\pi$ でもいい。 何か実数をひとつ選ぶと、数直線上の一点になる。 そして、条件を成り立たせる実数をすべて集めると、それは数直線上の点の集まりになる……点の集合、 つまり図形だよね」

テトラ「はい、そうですね」

僕「数式だけで考えるんじゃなく、図形を使って考えた方が《うっかりミス》は防げることが多い」

テトラ「確かにそうです」

僕「《$x \geqq 0$ という条件》と、《$x \geqq 0$ という条件を成り立たせる実数の集合》をある意味で同一視しているといえるかなあ」

テトラ「同一視……同じものと見なす、ですか」

僕「そう。条件を数式として考えるのと、点の集合……図形として考えるのを自由に行き来して考えることができるなら、 ややこしい問題でも取り組みやすくなるかもね」

テトラ「自由に行き来……あっ、これはあれですね！」

僕「どうしたの？」

テトラ「先輩から教えていただいた《二つの世界》のお話ですよね。 数式の世界と図形の世界を行ったり来たりする。 それは条件のときも同じなんですね」

僕「ああ、そうだね！」

テトラ「それに！　言葉の世界と数式の世界という《二つの世界》もありますっ！」

僕「うんうん、確かに」

テトラ「《$x$ は $0$ 以上》という言葉を《$x \geqq 0$》という数式で考えるのは、 《二つの世界》を行ったり来たりです」

僕「テトラちゃんはよく条件をまちがえたり忘れたりするっていうけど、 そういう二つの世界を意識していると、まちがってないかどうかチェックしやすくなるかもね」

テトラ「……！」

僕「ほら、たとえまちがえたとしても、そのまちがいを見つけられるなら、直せるかもしれない。 だから、まちがえそうな世界から、別の世界に移ってチェックするんだよ」

テトラ「……なるほどですっ！」

僕「じゃあ、ちょっと複雑な条件で試してみようか」

テトラ「ええっ！」

僕「こんな問題はどうかな。いいかい……」