第39回 シーズン4 エピソード9

サイコロ娘の極限値（前編）

僕の部屋

ユーリ「お兄ちゃん、それなに？」

僕「ああ、これ？　学校の先生に借りたんだよ」

ユーリ「これは……ずいぶん大きなサイコロ！　でもへんなの。何これステンレス？　もっとよく見せてよ」

僕は手のひらにすっぽり入るくらいの大きさの「それ」をユーリに渡した。

僕「何かは知らないけど、金属なのはまちがいないよ」

ユーリ「あれ、意外と軽い！　変なサイコロ！　丸い輪がくっついて出っ張って「目」になってるんだね。ふつーは、くぼんでるよね？」

僕「そうだね。でも、このサイコロの変わっているところはそこじゃないんだよ」

ユーリ「へ？　どーゆーこと？」

僕「よく見てごらんよ」

ユーリはサイコロをくるんと回す。

ユーリ「あれれ？　何これ、サイコロじゃないじゃん！」

僕「気づいたか」

ユーリ「いやいやいやいや、ふつーすぐ気づくって！」

僕「そう？」

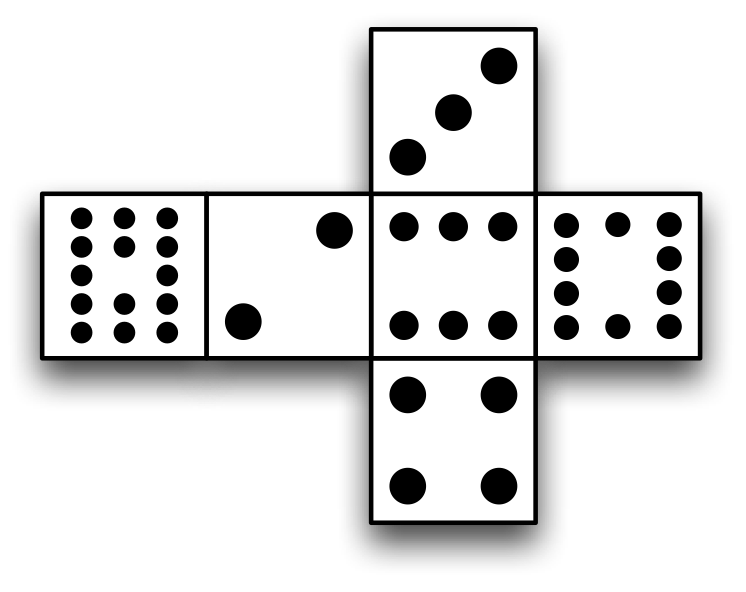
ユーリ「そうだよー！　うわ、なにこれキモい。 $3$ はいいけど、これは何の目……えっと $1,2,\cdots,10$ だから、上は $10$ の目だね。 それでこっちは…… $14$ の目だ！　目の数が多いの、すごいイワカン」

僕「そうだね。これは、 $10$ の目や $14$ の目があるサイコロなんだ」

ユーリはサイコロをくるくる回しながら、興味深げに各面を見ている。

ユーリ「普通のサイコロにある $1$ と $5$ の目がないみたい」

僕「そうだね。ねえ、ユーリは《サイコロの目の規則》って知ってる？」

ユーリ「足して $7$ だよね」

僕「そうそう」

ユーリ「だったら知ってるよー」

僕「そうだね。普通のサイコロなら、裏面の目との和は $7$ になる」

ユーリ「ねー、でも、この変なサイコロは違うよ。 $3$ の裏面が $4$ なのだけは合ってるけど」

僕「そうだね」

ユーリ「えーと、 $6$ の裏面は $1$ じゃなくて $14$ になってる。 それから $2$ の裏面は $5$ じゃなくて $10$ になってる」

ユーリはサイコロを注意深く回転させて答えた。

僕「うん」

ユーリ「ところで、このサイコロはいったい何なの？　先生に借りたってどゆこと？」

僕「お兄ちゃんの高校に《村木先生》という先生がいるんだけど、 ときどき数学の問題を出してくれるんだ。学校の授業とは関係なく」

ユーリ「ふーん」

僕「このサイコロはその先生に貸してもらったんだよ」

ユーリ「これで何かゲームでもするの？　 $10$ や $14$ が出たら大きいね」

僕「特に何か決まったことをするわけじゃないんだけど。 《これで何かおもしろいこと考えてごらん》という研究課題なんだよ」

ユーリ「この変なサイコロで？　おもしろいことを考える？」

僕「うん。何でもいいから」

ユーリ「そんで？　お兄ちゃんは何か考えたの？」

僕「いや、まだだよ。さっき考え始めたばかりだしね。 お兄ちゃんは、まず展開図を描いてみたんだ」

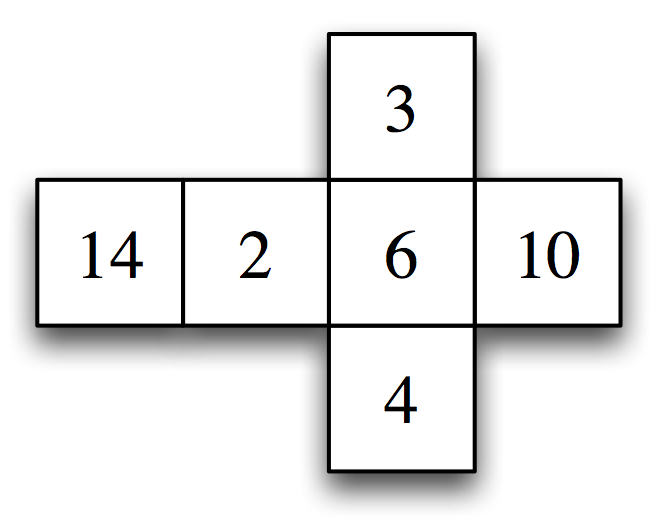
ユーリ「展開図って……これのこと？」

「僕」が作った展開図

僕「うん、そうだよ。これで何かおもしろいことが見つかるかな、と思って」

ユーリ「……お兄ちゃん、これまちがってるよ！」

僕「え？　そんなことないよ」

ユーリ「まちがってるって！　正しくは……こうだよん」

ユーリが作った展開図

僕「ん……同じじゃないか」

ユーリ「目の向きをよく見てほしいにゃ。お兄ちゃんの描いた展開図だとこのサイコロとおんなじものにはならないよん」

僕「ユーリ……まあ確かにそうだけど、普通はサイコロ考えるときには目は数として考えるよね」

ユーリ「へへ。ところでさー、この展開図見てたらエヴァのリリスを思い出しちゃった。 あれもキモかったよね。ロンギヌスの槍を」

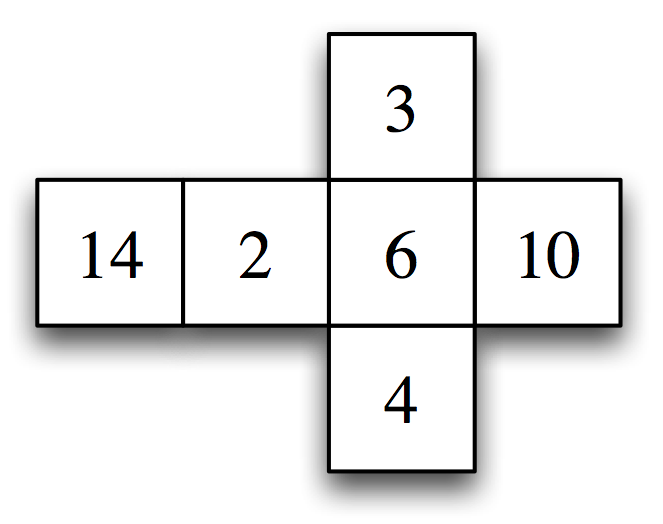
僕「そんな小ネタはいいから。まぎらわしいから展開図の目を数で置き換えよう」

目を数で置き換えた展開図

僕とユーリはしばらく無言で展開図を眺める。 何も言わないけれど、僕もユーリも頭はくるくると回転している。

どんなことでもいい。何かおもしろいことはないか？

僕「何か気づいた？」

ユーリ「んー《$3$ が惜しい》って感じかにゃ……って。ほら《$3$ 以外は全部偶数》じゃん？」

僕「そうだね。それもそうだけど、数の並びもあるし……」

ユーリ「並び？」

僕「うん、ほら、ただでたらめに数が散らばっているんじゃなくて、意味があって配置されるんだと思うんだよ。数が並べられている」

ユーリ「この展開図で数列を作るってこと？」

僕「お？」

ユーリ「だって、数が並ぶって数列ってことでしょ？」

展開図で数列を作る

僕「そうかそうか、それはおもしろいな。数列ならまず《階差数列》を作って……」

ユーリ「$14, 2, 6, 10$ だと、引き算して $-12, 4, 4$ だね」

僕「ん？　いや違うよ、ユーリ。 $14$ を、右にぐるっと回したほうがおもしろそうだ。 $2, 6, 10, 14$ になるから階差数列は $4, 4, 4$ だ！」

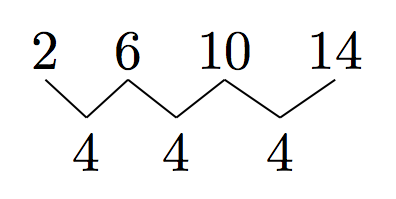
ユーリ「おー！」

僕「階差数列が同じ数の並びになる。つまりこれは等差数列だ……まあ、でも、だから何だという話だけどね」

ユーリ「……」

僕「どうした？」

ユーリ「この縦の $3, 6, 4$ は何とかなんないの？　階差数列は $3, -2$」

僕「そうだなあ……だけど、 $3$ 個の数で階差数列を作っても《こじつけ》っぽいかな」

ユーリ「コジツケって？」

僕「てきとうな理屈はいくらでもつけられる、ってことだよ」

ユーリ「だって、おもしろいことなら何でも考えればいいっていったじゃん！」

僕「まあ、そうか。うん、そうだね。こじつけでもいいか」

ユーリ「ユーリはね、《$3$ だけが奇数》っていうのが気になってるんだよ」

僕「ふむ。あ、じゃあ《$3$ は $6$ を半分にしたもの》って考えたら？」

ユーリ「お兄ちゃん、あったまいー！　……すごいこじつけ」

僕「あはは」

ユーリ「あ！！！」

僕「わ！！！……どうした、ユーリ？」

ユーリ「だったらさー、 $2$ や $10$ や $14$ も半分にしたら？」

僕「？」

ユーリ「$1$ や $5$ や $7$ を上に乗っけて、こーゆー表にしちゃうの！」

僕「ほう！　なるほど。サイコロの展開図からもう離れるってこと？」

ユーリ「それでも、いーんでしょ？」

僕「もちろん。何も問題はないよ。ユーリの思う通り、何でも書いてごらんよ」

ユーリ「これで $3$ は解決したよ！」

僕「ふむ……」

ユーリ「でも今度は下の $4$ が仲間はずれになった……ねえお兄ちゃん」

僕「そうだね……」

ユーリ「$1,3,5,7$ は奇数で横並びになった。 それから $2,6,10,14$ は等差数列。でもその下に $4$ が出っ張ってる」

僕「ユーリ、この $4$ を動かしてみよう。この表の $4$ は左に動かせる。 $4$ を左に動かしても、展開図としては正しい。 あの変なサイコロは作れるはずだ」

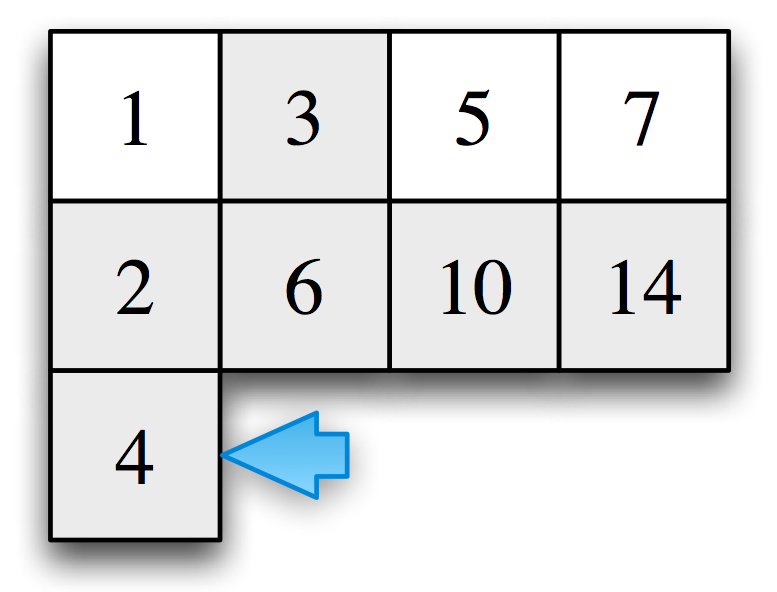
ユーリ「あ！」

僕「ね？」

ユーリ「お兄ちゃん！　わかったわかった！　右下のあいてるところ $3$ つ、埋められるね！」

僕「そうだね」

ユーリは急いで表の空きを埋めた。

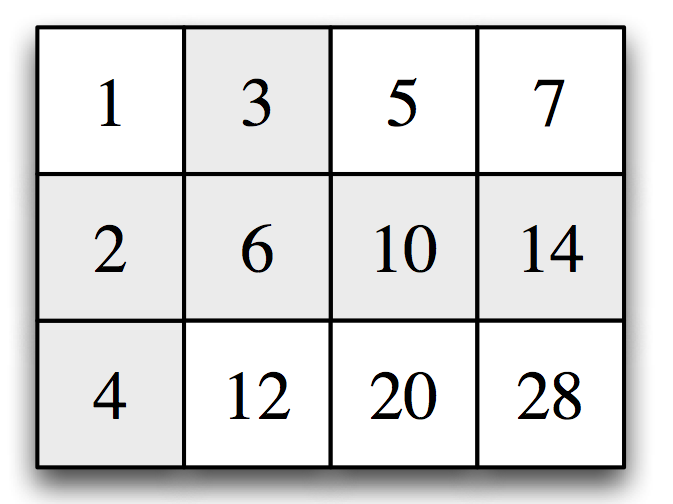
ユーリ「これで《いい》よね！」

僕「おもしろいな。ユーリはおもしろい表を作ったね」

ユーリ「あのね、 $1$ 行目は $1,3,5,7$ で「$2$ ずつ」増えるでしょ？　 そして $2$ 行目はその $2$ から始まって $2,6,10,14$ になるから「$4$ ずつ」増えてる。 そして $3$ 行目はこんどその「$4$」から始まって $4, 12, 20, 28$ だから、「$8$ ずつ」増えるんだよ。 これっておもしろい規則じゃない？！」

$1$ 行目は、 $1$ から始まって「$2$ ずつ」増える

$2$ 行目は、 $2$ から始まって「$4$ ずつ」増える

$3$ 行目は、 $4$ から始まって「$8$ ずつ」増える

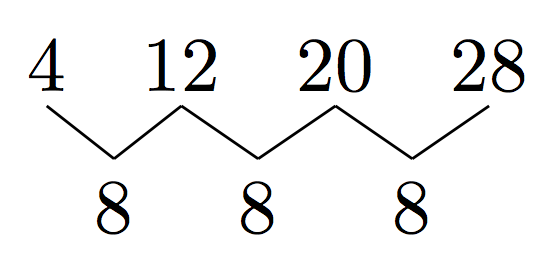
僕「ユーリのその規則はずっと続けられるね」

ユーリ「うん、ずっとずっと無限に続けられるよ！」

僕「うん、なかなかおもしろい表だな」

ユーリ「この表はこーなってるんだよ。左側に $1,2,4,8,16$ って $2$ 倍になる数を縦に並べるっしょ？」

僕「うん」

ユーリ「それで、その数から始めて、右側に数を伸ばすんだけど、階差数列に出てくる数が、次の行の先頭の数なの」

僕「なるほど、ユーリの規則でもこの表はできるね」

ユーリ「なにその引っかかる言い方。なんかおかしい？」

僕「いやいやおかしくないよ。同じことなんだけど、お兄ちゃんだったらこう言うよ。 《いちばん上の行に $1,3,5,7,9,\ldots$ っていう奇数の列を並べておく。 そして下に伸ばすときには上の数を $2$ 倍にする》ってね」

ユーリ「それってユーリと同じこといってるじゃん！」

僕「でも、お兄ちゃんの言い方の方がシンプルじゃない？　《$1$ 行目に奇数の列、下に行くには $2$ 倍》という一言で済む」

ユーリ「……なんかくやしーな」

僕「縦に並んだ数は《初項が奇数で公比が $2$ の等比数列》であるとも言えるよ。 同じ表でも、いろんな言い方があるから、ユーリの言い方でもいいんだよ」

ユーリ「いいもん！　もっとおもしろい言い方考えるもん！」

ユーリは真剣な顔をして数表をにらむ。栗色のポニーテールが金色に輝く。

僕「……」

ユーリ「ふっふっふ。これならどうだ！　上に奇数の列、左に $1,2,4,8,\ldots$ で、この表は《かけ算の表》なの！」

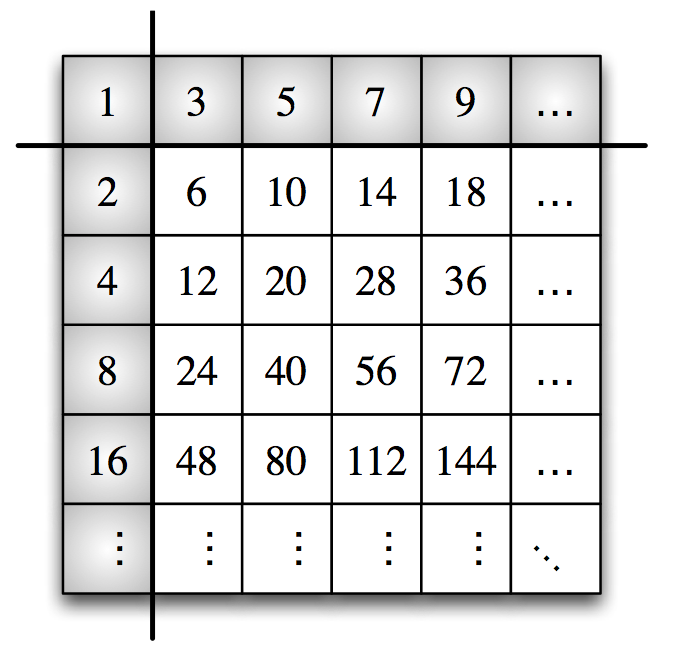
僕「おお！　それもわかりやすいな！」

ユーリ「ふふん」

僕「確かにそうなっているなあ」

• $1$ 行目は奇数の列。
• $1$ 列目は $2$ の冪乗（べきじょう）。
• 表全体は行と列のかけ算（奇数と $2$ の冪乗の積）。

ユーリ「ねー、ユーリもすごいっしょ？」

僕「すごいすごい……ところで、ユーリの説明で、気がついたことがある。この表はすごいよ」

ユーリ「何がすごいの？」