第35回 シーズン4 エピソード5

いとしのフィボナッチ（前編）

$1024$ の謎

ユーリ「お兄ちゃん、あそこに広告あるじゃん？」

僕「ん？　どれのこと」

ユーリ「あそこの広告！　《$1024$ 通りものパターンが楽しめます》」

僕「あるね……あれは何の広告？　新しいゲーム？」

ユーリ「それはどーでもいいの。どして《$1024$ 通り》なんて中途半端な数にするの？　 $1000$ 通りでいいじゃん」

僕「ああ、そういう話？　 $1024$ に限らず、中途半端に見える数はときどき見かけるよね。 $64$ ビットとか」

ユーリ「そーいえばそーだね」

僕「あれは $2$ の冪乗（べきじょう）なんだよ」

ユーリ「にのべきじょう？」

僕「うん。 $2$ の累乗（るいじょう）ということもあるよ」

ユーリ「ふーん」

僕「$2$ の冪乗っていうのは、簡単に言えば《$1$ に対して $2$ を何個も掛けて作った数》だね。 たとえば、 $1024$ というのは、《$1$ に対して $2$ を $10$ 個掛けて作った数》になる」

$$ 1024 = 1 \times \underbrace{2 \times 2 \times 2 \times \cdots \times 2}_{\REMTEXT{$10$個}} = 2^{10} $$

ユーリ「そーなんだ」

僕「最初は $1$ がある」

$$ 1 $$

ユーリ「……」

僕「その $1$ に対して、 $2$ を $1$ 個掛けたら、 $2$ になるよね」

$$ 1 \times \underbrace{2}_{\REMTEXT{$1$個}} = 2 $$

ユーリ「うん」

僕「$1$ に対して、 $2$ を $2$ 個掛けたら、 $4$ になる」

$$ 1 \times \underbrace{2 \times 2}_{\REMTEXT{$2$個}} = 4 $$

ユーリ「そーだね」

僕「それを繰り返していくと、 $1, 2, 4, 8, 16, 32, 64, \ldots$ になる」

ユーリ「あ、ほんとだ。 $64$ が出てきた」

僕「もっと繰り返すと、 $128, 256, 512, 1024, \ldots$ になるね。 要するに $2$ の冪乗は、 $2^n$ という形をした数ということだね。 $n = 0, 1, 2, 3, 4, \ldots$ として」

ユーリ「あれ？　 $2^0$ って $1$ になるんだっけ」

僕「そうだね。 $2^0$ は $1$ に等しいよ。 $1$ に対して $2$ を $0$ 個掛けた数だね」

$$ 1 = 2^0 $$

ユーリ「ふんふん」

僕「ほんとうは、指数法則を使ってきちんと定義しなきゃいけないんだけどね」

ユーリ「でも、どーしてその……えっと、《$2$ のべきじょう》が出てくんの？」

僕「コンピュータに関係した数なんだよ。 コンピュータはオンとオフの $2$ 通りを何個も組み合わせて計算するよね。 だからコンピュータに関わる数には《$2$ の冪乗》がよく出てくる。 $1, 2, 4, 8, 16, 32, 64, \ldots$ ってね」

数列の研究

ユーリ「ふーん……あ！　そーだ！　こないだお兄ちゃん《数列》の話してくれたじゃん？」

僕「え？」

ユーリ「ほらほら。お兄ちゃんがボロ負けしたとき、オセロで《階差数列》の話したじゃん！（第32回参照）」

僕「その思い出し方やめてくれないかな……そうだったね。階差数列は大事だよ。 数列について調べたいと思ったら、 隣り合った二つの項の差を計算してできる数列——階差数列を使うことは定石になる」

ユーリ「うん、確か『数列を研究するなら、その《階差数列》を研究するんだよ、美しいユーリ』って教えてくれたよね、お兄ちゃん」

僕「よけいな形容詞いれなくていいから」

ユーリ「$1, 2, 4, 8, 16, 32, 64, \ldots$ ってゆーのも数列だよね？」

僕「そうだね。数を並べたものは何でも数列だから、これも立派な数列だよ」

ユーリ「そんじゃ、これも階差数列で研究できるじゃん！　えーと、 $2 - 1 = 1$ で、 $4 - 2 = 2$ で、 $8 - 4 = 4$ で……あれれ？」

僕「どうした？」

ユーリ「なんかおかしい！　変わんないよ、お兄ちゃん！」

僕とユーリはエレベータそばのソファに座り、チラシの裏に数列を書く。 僕たちはどこでも数学トークを始めるのだ。

僕「何がおかしいの？」

ユーリ「ほらほら。 $1, 2, 4, 8, \ldots$ の階差数列を取ると、 $1, 2, 4, 8, \ldots$ になっちゃうよ。元のままじゃん！」

僕「なるほど。確かにそうだね。すごい発見だ」

ユーリ「こないだお兄ちゃんと階差数列で遊んだときは、こんなふうにはならなかったよ」

僕「ああ、そうだね。それは《等差数列》だったから。 等差数列は、各項の差が一定の数列だね。 $1, 3, 5, 7, 9, 11, \ldots$ の奇数列とか（第32回参照）」

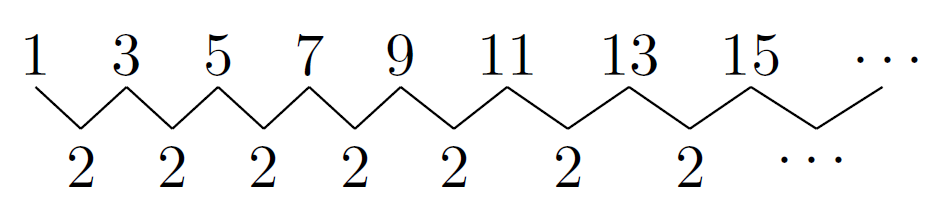
ユーリ「そかそか。 $1, 2, 4, 8, \ldots$ の方は等差数列じゃないんだ」

僕「うん。これは《等比数列（とうひすうれつ）》になる。 隣り合った二つの項の《差》が等しいんじゃなくて、《比》が等しい数列だね」

ユーリ「とうひすうれつ……」

僕「等比数列で《隣り合っている次の項》を作り出すときに何倍にするか——その数のことを《公比（こうひ）》というから、 $1, 2, 4, 8, 16, 32, \ldots$ は、最初の項（第 $1$ 項）が $1$ で公比が $2$ の等比数列になる」

ユーリ「ふーん……ねえ、お兄ちゃん」

僕「何？」

ユーリ「この等比数列 $1, 2, 4, 8, 16, 32, \ldots$ は階差数列を取るとおんなじ $1, 2, 4, 8, 16, 32, \ldots$ になるじゃん？」

僕「そうだったね」

ユーリ「等比数列って、階差数列はもとの数列と同じになるの？」

僕「その《ユーリの予想》はおもしろいな」

ユーリ「ちょっと待ってよ。《ユーリの予想》とか勝手に名前つけないでよ。お兄ちゃんに訊いただけじゃん！」

僕「ユーリはどうだと思う？」

ユーリ「え？　えーとね……」

僕「たとえば、別の等比数列を考えてみればいいよ。 たとえば第 $1$ 項が $2$ で公比が $3$ の等比数列——とかね」

ユーリ「公比が $3$ っていうのは、毎回 $3$ を掛けるんだっけ」

僕「そうそう。第 $1$ 項が $2$ で、そこに $3$ をどんどん掛けていって掛けて作る数列」

ユーリ「ってことは……えっと、 $2$ と、 $2 \times 3 = 6$ と、 $6 \times 3 = 18$ と……こうかにゃ？」

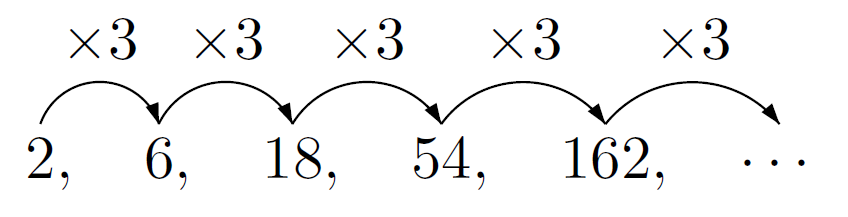
僕「そうだね。その数列の階差数列はどうなる？」

ユーリ「$6 - 2 = 4$ で、 $18 - 6 = 12$ で、 $54 - 18 = 36$ で……あ、元の数列と同じにならない！」

僕「そうだね」

ユーリ「そっか。じゃ、等比数列の階差数列はもとの数列になるとは限んないんだ」

僕「うん。ねえユーリ。ユーリはいま《数学の研究手順》を踏んだんだよ」

ユーリ「けんきゅーてじゅん……って、どゆこと？」

僕「ユーリは $2$ の冪乗が作る数列——第 $1$ 項が $1$ で公比が $2$ の等比数列——を見て、予想を立てたよね。 《等比数列の階差数列は、もとの数列に等しくなる》という《ユーリの予想》だ」

ユーリ「お兄ちゃんが勝手に名前つけたんだけどね！　しかも、まちがってたし！」

僕「まあ、そうなんだけど、 自分で疑問を持って《これはこうなるのかな？》みたいに予想を立てるのはとても大事なことなんだよ」

ユーリ「ふーん」

僕「予想を立てて、さらにその予想が正しいかどうか確かめようとした。 これは数学者がやっている《数学の研究手順》と基本的には同じなんだよ」

ユーリ「なんか大げさな話になってきたにゃ」

僕「数学者も予想を立てる。そしてその予想が正しいかどうかを確かめようとする。 数学的に正しいということを示すには証明をしなくちゃいけない。 あるいは予想が誤りであるということを証明してもいい。 こちらは反証ということもある」

ユーリ「証明と反証って……ユーリ、どっちもやってないよ？」

僕「いやいや。ユーリは《第 $1$ 項が $2$ で公比が $3$ の等比数列の、階差数列》を調べてみた。 そしてそれがもとの数列になっていないことを確かめた。 つまり《予想が誤りであるという具体例を示した》わけだよね。 これも立派な証明——この場合は予想の反証——になるんだよ」

ユーリ「へー……」

僕「予想をくつがえす例のことを《反例（はんれい）》というよ。 だから、 $2, 6, 18, 54, \ldots$ という等比数列は《どんな等比数列も、階差数列をとると同じ数列になる》という 予想の反例になっているといえるね」

ユーリ「はんれい——それって例を一個みつければいいの？」

僕「そうだよ。予想に反する例を見つけたら、それが反例になるね」

ユーリ「ふーん。数学者……予想を立てて証明か反証……反例を見つける……か」

一般的に考える

僕「等比数列をもう少し研究してみよう。等比数列を一般的に表現するよ」

ユーリ「どゆこと？」

僕「等比数列というのは、 $a, ar, ar^2, ar^3, \ldots, ar^{n-1}, ar^n, \ldots$ のように一般的に書けるよね」

ユーリ「ちょっと待ってよ、お兄ちゃん。いきなり $a$ とか $r$ とか出さないでよ」

僕「ごめんごめん。等比数列の第 $1$ 項を $a$ という数だとする。 $a$ は実際は数なんだけど、一般的に考えるために $a$ という文字を使う。 それから、公比を $r$ とする。そうすると、等比数列は、 $a$ に対して、何回も $r$ を掛け算して作ったものだと考えることができる。 一般的に表現した等比数列だね」

ユーリ「えーと、ちょっと待ってよ……うん。だいたいわかった」

僕「$a$ を $ar^0$ と書いて、 $ar$ を $ar^1$ と書くと、もう少しきれいに書ける」

ユーリ「何がきれーなの？」

僕「等比数列の第 $n$ 項はいつでも、 $ar^{n-1}$ という形をしているってわかるからだよ」

ユーリ「？」

僕「《その数列、第 $n$ 番目の項はなに？》と聞かれたときに《はいこれです》と言えたらうれしいんだよ。 その数列について調べるときに役立つから」

ユーリ「……」

僕「だから《第 $1$ 項が $a$ で公比が $r$ の等比数列。その第 $n$ 項は $ar^{n-1}$ と表せる》というのはうれしい。 だって、《第 $n$ 番目の項はなに？》と聞かれたら、 $ar^{n-1}$ を計算すればいいだけだからね」

ユーリ「あれ……ねえお兄ちゃん。それ、さっきも似たよーな話してなかったっけ」

僕「ああ、そうだね。さっきは $a$ や $r$ という文字を使って等比数列を一般的に表現した。 今度はさらに $n$ という文字を使って、等比数列の第 $n$ 項を表現した。 実際、この第 $n$ 項のことは数列の《一般項》ともいうんだよ」

ユーリ「いっぱんこう……文字が出てくるといつも一般的になるんだね」

僕「そうそう！」

《ユーリの予想》の修正

ユーリ「ねえお兄ちゃん。 いーんだけどさ、そもそもなんで《いっぱんてきにひょうげん》すんの？」

僕「うん。全部まとめて扱いたいからだよ」

ユーリ「まとめて？」

僕「ほら、等比数列とひとくちにいっても、第 $1$ 項と公比の組み合わせで無数の等比数列が作れるよね。 でも、文字を使って一般的に表現すれば、無数の等比数列をいっぺんに扱うことができる。 たとえば、 $a = 1, r = 2$ にすれば、 $1, 2, 4, 8, \ldots$ が得られるし、 $a = 2, r = 3$ にすれば、 $2, 6, 18, 54, \ldots$ が得られるよね」

ユーリ「え……まー、そっか」

僕「それでね、さっきの《ユーリの予想》を修正できないかな、と思っているんだよ」

ユーリ「修正って？」

僕「等比数列の階差数列はもとの数列になる——という《ユーリの予想》は残念ながら誤っていた。 でもね、《等比数列の階差数列がどういう形をしているか》を考えることはできる」

ユーリ「んんん？　意味わかんない。 《等比数列の階差数列》なんてそれこそ無数に作れるんじゃないの？　意味わかんない。 どういう形をしているかバチッとわかるわけないじゃん」

僕「大丈夫。僕たちは武器を持ってるから。《文字を使う》という武器だよ。 《等比数列の階差数列》は無数に作れるけれど、もしかしたら、同じ形になるんじゃないかな？」

ユーリ「あっ！　そゆことか。具体的な階差数列じゃなくて？」

僕「そうそう。一般的に表現した等比数列を使って、階差数列を作る。 そのとき、階差数列はどんな形をしているかな？ 文字を使って考れば、無数の等比数列をいっぺんに扱うことができるよ」

ユーリ「そっか！　ユーリにもできるかな？」

僕「できると思うよ。《一般的に表現した等比数列の階差数列》を求めよう」