第34回 シーズン4 エピソード4

驚異のシグマ（後編）

素朴な疑問

テトラ「先輩、ふと思ったんですけど」

僕「なに？」

テトラ「どうして——いったいどうして、わざわざ $\sum$ があるんでしょうね」

僕「え？　どういう意味？」

テトラ「ええっとですね、足し算をするなら、 $+$ という記号があるわけですよね。すでに」

僕「まあそうだね」

テトラ「なのに、わざわざ、 $\sum$ を使って和を表すのはどうしてなんでしょう？　もしも $a_1 + a_2 + a_3$ という和を表したかったら、 そう書けばいいですよね。なのにわざわざ $\sum$ を使うのは——？」

$$ \sum_{k=1}^{3} a_k = a_1 + a_2 + a_3 $$

僕「なるほど……それは、なかなか深い質問だよ、テトラちゃん。いつもながら」

（しかも……答えるのがむずかしい質問だなあ）と僕は思った。

そして——僕は考える。 僕は自主的に数学の本を読み、 $\sum$ の扱いも本で学んだ。 $\sum$ が複雑に見えるのは確かだ。 『どうして $\sum$ を使うのか』とテトラちゃんが思うのも理解できる。 でも、でも、どう話せばテトラちゃんにわかってもらえるのだろう。 そもそも僕は、 $\sum$ の役割を本当にわかっているんだろうか……。

僕「……」

テトラ「先輩？」

僕「うん、ちょっと考えてたんだ。そうだなあ……」

テトラ「ちょっと待ってください、先輩。あたしも考えてみます、 $\sum$ を使って和を表す理由。 いつもいつもお聞きしてばかりでは、テトラがすたります」

僕「なるほど」（テトラがすたる？）

テトラ「そうですねえ……たとえば、こういう理由はいかがですか。実は $\sum$ には驚くべき秘密がある」

僕「秘密？」

テトラ「つまり、プラス（$+$）はただの足し算だけれど、シグマ（$\sum$）はただの足し算じゃない！　などという理由です」

僕「うーん、それはないと思うなあ。たとえば、この式を考えてみると……」

$$ \sum_{k=1}^{3} a_k = a_1 + a_2 + a_3 $$

テトラ「はい」

僕「この式には何も隠れているところはない。秘密は何もないよ。 $\displaystyle \sum_{k=1}^{3} a_k$ というのは、 《整数を表す変数 $k$ を $1$ から $3$ まで動かして $a_k$ の和を作る》ということ。 $a_1+a_2+a_3$ とまったく同じことになるよ、テトラちゃん」

テトラ「そうですか……そうですよね」

僕「ねえテトラちゃん。そもそも、シグマとプラスは両方とも和を表すけれど、その表現方法が違うよね。 それでもうテトラちゃんの疑問に答えているんじゃないのかなあ」

テトラ「といいますと？」

僕「たとえばさっきの例でいうと、 $\displaystyle\sum_{k=1}^{3} a_k$ はコンパクトにまとまった数式だし、 $a_1 + a_2 + a_3$ は長くなってしまうけれど式の全体像がよくわかる数式だよね」

テトラ「はあ……」

僕「だから、シグマを使いたいときと、プラスを使いたいときのどちらがあってもいいんじゃないかなあ」

テトラ「は、はい。それは先輩のおっしゃる通りかもしれません。でも、まだ……」

僕「まだ、しっくり来ない？」

テトラ「そうですね。すみません。シグマを使っていると《難しい数式だゾ》と誰かに言われている気持ちになります。 《レベルが違うんだゾ》みたいに」

テトラちゃんが急に「……だゾ」とお化けみたいな声音を出すので、 僕は思わず笑ってしまいそうになる。

僕「確かにね。慣れないと難しそうに見える」

テトラ「ですから、もしも同じ和を表すのなら、シグマを使わずにプラスを使って表したほうがわかりやすいなあ……って」

僕「ふむふむ」

テトラ「あ、ミルカさぁん！」

テトラちゃんは急に図書室の入り口に向かって手を振った。 長い黒髪の饒舌才媛こと、ミルカさんの登場か。

ミルカさん

ミルカ「便利だから」

ミルカさんはテトラちゃんの疑問を聞くとそんなふうに即答した。

僕「$\sum$ を使う理由は……便利だから？　それはまた身もふたもない理由だね」

テトラ「便利だから、ですか……」

ミルカ「そしてもちろん、どう便利なのか、が次の疑問になる。そうだね、テトラ？」

テトラ「あ、は、はい、その通りです。いまそれをお聞きしようと思っていました」

テトラちゃんは挙げかけた手を下ろす。

ミルカさんは半ば歌うように話し出す。

ミルカ「数式は言葉。 言葉は表現の道具。 言葉は思考の道具。 道具を磨き、表現を磨く。 道具を磨き、思考を磨く——そうだね、テトラ」

テトラ「はい、そうだと思います」

ミルカ「シグマを使うか、プラスを使うか。そこに意味の相違はない。どちらも和だ」

テトラ「はい、でも……」

ミルカ「しかし、意味の相違はないとしても、数式は言葉だ。 表現上の相違が思考上の相違を生むことはありえる」

僕「抽象的だなあ」

ミルカ「ふうん……」

ミルカさんは僕のつぶやきを冷たくあしらう。

テトラ「ミルカさん、あたしが知りたいのは《そこ》です！　そこが知りたいです。 シグマを使うことでどんな《相違》が生まれるんでしょう」

ミルカ「たとえば、和の操作」

テトラ「和の操作？」

僕「和の操作？」

和の操作

ミルカ「そう」

ミルカさんさんは、僕とテトラちゃんの顔を交互に見て微笑み、話を続けた。

ミルカ「私たちが和を計算するとき、 $\sum$ は便利な道具だ。 特に《和の操作》を行うために便利だ。それは、 $\sum$ は《和の構造》をあらわに見せてくれているからだ」

テトラ「和の操作……和の構造……それはいったいなんでしょう」

ミルカ「簡単な話から始めよう。私たちは《$a_1$ から $a_n$ までの和を $S$ と置く》などとして変数を定義する場合がある」

僕「そうだね。何かを$S$と置く、何かを$S$と定義する、$S = \REMTEXT{なんとか}$とする……いろんな言い方があるよね」

ミルカ「しかし、 $S$ には $n$ が顔を出していない」

テトラ「……」

僕「$a_n$ までの和なら、普通は $S_n$ と書くと思うけど」

ミルカ「そうだ。 $S$ ではなく $S_n$ と書くことが多い。それは、 $S$ では有効な操作ができないから」

テトラ「ミルカさん……その《操作》という言葉の意味がよくわかりません」

ミルカ「もう少しすればわかってくる」

テトラ「はい……」

ミルカ「$S$ なら操作できない。 $S_n$ なら操作できる。 たとえば、 $a_1$ から $a_3$ までの和は $S_3$ と表現できる。 $a_1$ から $a_{100}$ までの和は $S_{100}$ と表現できる」

テトラ「ははあ、添字のところを変えられるということですね」

ミルカ「さらに、《$S_3$ に $a_4$ を加えた結果は $S_4$ に等しい》などと表現することもできる」

僕「ミルカさんは、パラメータが表記に現れているということをいってるの？　 $S$ と書くと、 $n$ というパラメータが見えなくなっちゃうけど、 $S_n$ と書けば $n$ というパラメータが外に見えるようになるってこと？」

ミルカ「そう。そして、同じことが $\sum$ についてもいえる」

テトラちゃんがさっと手を挙げる。

テトラ「す、すみません。ミルカさん。何がどう同じなのかがわかりません。 $S_n$ のように表現すれば、 $S_3$ や $S_{100}$ みたいに書けるというのはわかりましたが、 それと $\sum$ の関係がわかりません。それに《操作》という言葉も……飲み込み悪くてすみません」

ミルカ「ふうん……それでは、プラスとシグマを比較して話をしていこう」

テトラ「お願いします」

プラスとシグマ

ミルカさんさんは、一瞬目を閉じ、テンポを落として話し始めた。

ミルカ「私たちはいま、和——数列の和に関心がある。 ある数列の $a_1$ から $a_n$ までの和——これを数列の部分和という——を取り扱いたい。 数列の部分和を表すのに二つの方法を考えている。一つはプラスを使って表す方法」

テトラ「はい」

ミルカ「そして、もう一つはシグマを使って表す方法」

ミルカ「まず大前提として、テトラのいうようにプラスを使った方がわかりやすい場合があるのは確かだ。 何でもシグマで書けばいいというものではない」

僕「プラスだと全体像がわかるしね」

ミルカ「そうだ。プラスを使う方法はテトラもよくわかっているから、 いまはシグマに注目しよう」

僕「シグマはコンパクトに書けるなあ」

ミルカ「それも一つある。しかし、まずはシグマに何が書かれているかに注目しよう」

僕「何が書かれているか？」

ミルカ「そうだ。シグマには、和の構造が明示的に書かれている——ここが肝心だ」

テトラ「和の構造……あ、和の本体 $a_k$ のことですか？」

ミルカ「それだけではない。和の本体、整数の添字、添字の下限、添字の上限だ」

$\sum$ に書かれている和の構造

• 和の本体（ここでは $a_k$）
• 整数の添字（ここでは $k$）
• 添字の下限（ここでは $1$）
• 添字の上限（ここでは $n$）

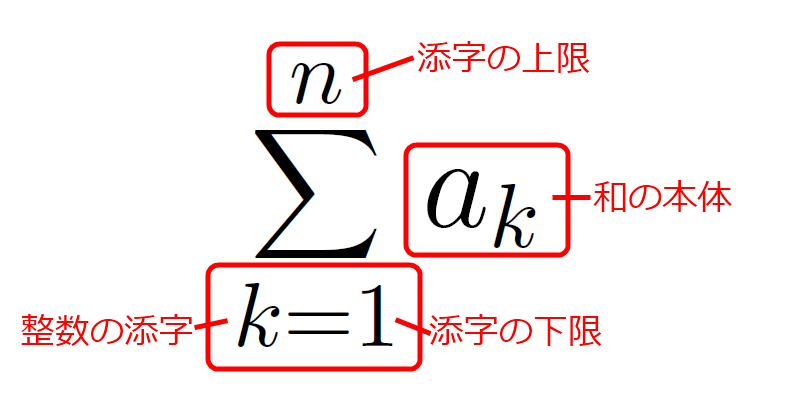
僕「確かに……改めて考えると、シグマのまわりには和がどんな構造をしているかが書かれているわけか」

ミルカ「シグマを使って、私たちはさまざまな和を統一的に表現することができる。いくつか例を挙げよう」

ミルカ「ここでは、整数の添字 $k$ を下限の $1$ から上限の $3$ まで変化させて、和の本体である $a_k$ の和を求めている」

テトラ「はい、よくわかります」

ミルカ「上限を増やすだけで、より多くの項を足し合わせられる。たとえば $3$ を $5$ に変える」

僕「まあ、そうだね」

ミルカ「さらには、すべてを列挙して書くのが難しい和も作れる——シグマの上限を変えるだけだ。たとえば $100$ に変える」

ミルカ「$100$ 個の和なら、原理的には「$\cdots$」を使わずとも書ける。 しかし、 $n$ 個の和になると、途中に「$\cdots$」がどうしても入る。 何個列挙すればいいか具体的に定まらないからだ。 しかし、シグマならいつも同じ書き方ができる」

テトラ「確かにそうですね」

テトラちゃんは数式をじっくり眺めながらコクコクとうなずいた。

テトラ「シグマが和を表現する方法として統一感があるのは理解できました。 でも、あの、ミルカさんが先ほどおっしゃっていた《操作》があたし、気になって……そちらの方は？」

ミルカ「では、簡単なクイズを出そう。たとえば、シグマではこんな式変形ができる。これは何か」

テトラ「え……？」