第29回 シーズン3 エピソード9

まっすぐ進むまわり道（前編）

図書室にて

テトラ「先輩……いま、ちょっと、質問してもいいですか？」

僕「あ、ちょっと待って。ここまで書いちゃうから——はい、いいよ。テトラちゃん、何？」

テトラ「すみませんお勉強なさっているときに……先日、点の回転や三角関数について教えていただきましたよね」

テトラちゃんはいつもの《秘密ノート》を開きながら話し始めた。

僕「うん、そうだったね」

テトラ「あのとき教えていただいた内容はおもしろかったんですが、難しいところもあって……はい、 それで、あたし、もっと三角関数について勉強したいと思ったんです」

僕「テトラちゃんはえらいね。難しいと感じたときに《もっと勉強したい》って思うんだ」

テトラ「え……あ、はい。でないとあたし、どんどんわからないことがいっぱいあふれてしまうので」

僕「うん、それで、三角関数についての質問？」

テトラ「はい、そうです——といいますか、 三角関数って何をやっているのか、よくわからないんです。 参考書を見ていたら、たくさんたくさん公式が出てきて《あたし、こんなにたくさん覚えられない》って思って……」

僕「ああ、そうだね。三角関数はたくさん公式があるよね」

テトラ「こんなにたくさんの公式さんとお友達になれるんだろうか——と思ってしまいます。 しかもですね、その公式を説明している図がとっても複雑で、あたしは途方に暮れてしまって」

僕「うん、わかるわかる。 といってもいっぺんに全部の公式を使いこなすのは難しいから、慣れや練習も必要だよ。 そうだ、何か具体的に気になる公式ってある？」

テトラ「え……あ、はい。たとえば、そうですね。 三角関数の加法定理がよくわかりませんでした。ちょっと待ってくださいね。いまノートを……」

僕はテトラちゃんがノートを広げるよりも先に答える。

僕「うん、加法定理なら説明できるよ」

テトラ「え？」

加法定理

僕「加法定理ならすぐ説明できるよ。 $\sin$ の場合だと、こういう式になるよね」

テトラ「え！　さすがですね先輩！　どうしてそんなにさっと出てくるんでしょうか」

僕「うん、何度も書いているうちに覚えちゃったから。 参考書には語呂合わせを使った暗記方法もいろいろ書いてあるけど、 僕は《サイン・コス、コス・サイン》って頭の中で読んでる」

テトラ「え？」

僕「この式の右辺を見ると、 $\sin \alpha \cos \beta + \cos \alpha \sin \beta$ という形だよね。 角度の $\alpha$ と $\beta$ はいつもこの順番に固定しておいて、あとは $\sin \cdot \cos$（サイン・コス）と $\cos \cdot \sin$（コス・サイン） のように関数の順番だけを思い出せるようにしてるんだ」

テトラ「は、はあ……」

僕「自分で暗記方法を作った方が覚えやすいよ」

テトラ「そうなんですね」

僕「でも、文字の並びで丸暗記するだけじゃなくて、ちゃんと考えなくちゃ意味ないから注意してね」

テトラ「といいますと？」

僕「つまりね、 $\sin (\alpha + \beta) = \sin \alpha \, \cos \beta + \cos \alpha \, \sin \beta$ という 式が持っている意味を理解しないと、実際に使うことができないということ。 自分が問題を解いている途中で《お、これは加法定理が使えるんじゃないかな？》って気づけるかどうかが大切だから」

テトラ「なるほどです。加法定理の意味を理解するということですか……」

僕「うん。でも、式の意味というのは一つに決まるものじゃないよ。 《この式はこういう読み方もできる》みたいに、たくさんの意味があるんだ。意味というか、解釈というか。 式をいじっているとそういう読み方をいろいろ発見できるようになる。 それはとても楽しいよ」

テトラ「せ、先輩！　なんだか、あたし、先輩がすごくうらやましいです。 あたしもそういう《発見》をしてみたいです！　たとえば、この式はどう読むんですか？」

$$ \sin (\alpha + \beta) = \sin \alpha \, \cos \beta + \cos \alpha \, \sin \beta $$

僕「うん。発見といってもたいしたことじゃなくて、まあ当たり前のことなんだけど。 たとえばこの式の左辺を見ると、そこには $\alpha + \beta$ という二つの角度の和が出てくる」

$$ \sin (\underbrace{\alpha + \beta}_{\REMTEXT{和}}) = \cdots $$

テトラ「そういわれれば……確かにそうですね」

僕「$\alpha + \beta$ という加法、つまり足し算についての定理だから《加法定理》というんだね。 そして、加法定理の右辺を見ると、こちらには $\alpha + \beta$ は一つも出てこない。 $\alpha$ と $\beta$ はいつも分かれて登場するよね」

$$ \cdots = \sin \underbrace{\alpha}_{} \cdot \cos \underbrace{\beta}_{} + \cos \underbrace{\alpha}_{} \cdot \sin \underbrace{\beta}_{} $$

テトラ「うわ、そういえばそうですね……あらためて読み直すとなるほどです！」

テトラちゃんは僕が教えること一つ一つを真剣に聞き、全身全霊でそれに反応してくれる。 だから、ついついたくさんのことをテトラちゃんに教えたくなってくる。聞き上手というかなんというか……テトラちゃんは《教えられ上手》だなあ。

僕「だから、たとえば《$\sin \theta$ を求めることが難しい》という状況になったときに……」

• $\theta = \alpha + \beta$ のように、 $\theta$ が $\alpha$ と $\beta$ の和で表せる
• $\cos \alpha, \cos \beta, \sin \alpha, \sin \beta$ が求めやすい（すでにわかっている）

僕「……と見抜くことができたなら、加法定理が使えるわけだ」

テトラ「なるほどです！　それが加法定理の読み方なんですね！」

僕「うん。でもこれは読み方の一つの例だから気を付けてね」

テトラ「はい……と、ところで、そんなに都合がいい状況になるんでしょうか？」

僕「たとえば、 倍角の公式 $\sin 2\theta = 2\cos \theta \sin \theta$ は $2\theta = \theta + \theta$ と見抜けばすぐにわかるし、 それから、ええと、うん、たぶん $\sin x$ の微分をするときには、 $\sin (x + h)$ に対して加法定理を使うと思うよ」

テトラ「そうなんですか……」

テトラちゃんは、《秘密ノート》にメモをする。

僕「テトラちゃんはこの加法定理がよくわからなかったの？」

テトラ「はい……加法定理の説明の図が参考書に載っていたんですが、 とても複雑だったんです。がんばって理解しようと思ったんですが」

僕「うん、じゃあね、簡単な図を描きながら説明しようか。 いっしょにやればきっとわかるよ。 どうして加法定理で $\sin \alpha \, \cos \beta + \cos \alpha \, \sin \beta$ という式が出てくるのかもわかると思う」

テトラ「そうなんですか！」

僕「あ、そうだ。一般角について図で説明すると場合分けが入ってしまうから、 $\alpha$ も $\beta$ も $0^\circ$ より大きくて、 $\alpha+\beta$ が $90^\circ$ より小さいとして説明するね」

テトラ「はいっ！」

単位円から始まる

僕「これから加法定理 $\sin(\alpha + \beta) = \sin \alpha \, \cos \beta + \cos \alpha \, \sin \beta$ がどうして成り立つのかを 説明していくよ」

テトラ「はい、お願いします」

僕「まずは復習を兼ねて、《半径が $1$ の円（単位円）》と $\sin$（サイン）と $\cos$（コサイン）の関係を思い出してみよう」

テトラ「はい……」

僕「単位円の中心を回転の中心として、単位円上の点 $(1, 0)$ を、円周上 $\alpha$ だけ回転させたとするよね。 そのようすを図に描くとこうなる」

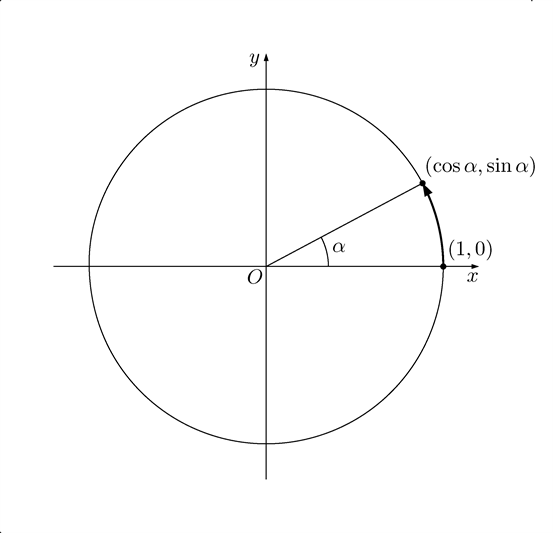
テトラ「はい、わかります。 $x$ 座標が $\cos \alpha$ で、 $y$ 座標が $\sin \alpha$ ですね」

僕「そうだね。これを $\cos$ と $\sin$ の定義だと思ってもいいよ。じゃあ、今度はテトラちゃんが $\beta$ だけ回転させてごらん」

テトラ「は、はいっ！　角度が $\beta$ なのですね……これでいいですか？」

僕「あ、ごめんごめん。僕の指示がよくなかったね。テトラちゃんがいま描いてくれたのは点 $(1, 0)$ を $\beta$ だけ回転させたんだよね」

テトラ「はい……何かまずかったでしょうか」

僕「いや、テトラちゃんの図はそれで正しいよ。僕が考えていたのはこういう図だったんだ」

テトラ「あ……これは回転を足したんですね」

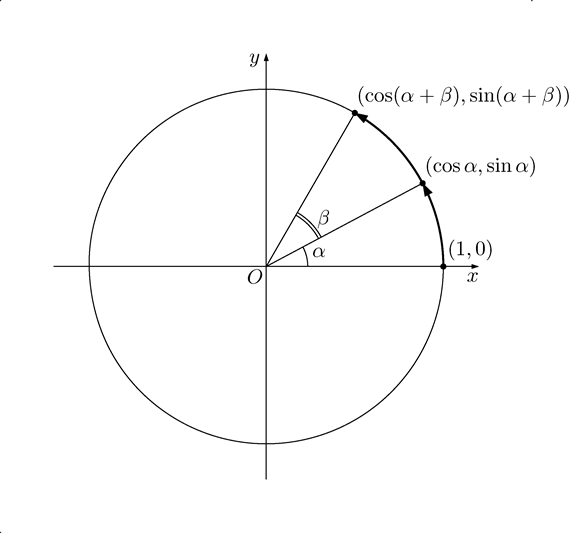
僕「そうそう。点 $(1, 0)$ を $\alpha$ だけ回転させると点 $(\cos \alpha, \sin \alpha)$ になる。 そして、その点をさらに $\beta$ だけ回転させると点 $(\cos (\alpha + \beta), \sin (\alpha + \beta))$ になる。 これは納得するよね」

$$ \begin{array}{cccccc} & \alpha & & \beta & \\ (1, 0) & \rightarrow & (\cos \alpha, \sin \alpha) & \rightarrow & (\cos (\alpha + \beta), \sin (\alpha + \beta)) \\ \end{array} $$

テトラ「はい、わかります。最初に $\alpha$ だけ回転させて次に $\beta$ だけ回転を足したら、 両方合わせて最初から $\alpha + \beta$ だけ回転させたのと同じということですよね。一気にぐうんと回転」

僕「うん、それでいいよ」

$$ \begin{array}{cccccc} & \alpha + \beta & \\ (1, 0) & \longrightarrow & (\cos (\alpha + \beta), \sin (\alpha + \beta)) \\ \end{array} $$

テトラ「それで、ここからどうなるんですか？」

僕「うん、ほら、ここを見てごらん。僕たちがいま興味があるのは $\sin (\alpha + \beta)$ という式だけど、 この回転後の点の $y$ 座標がぴったり $\sin (\alpha + \beta)$ になっているよね！」

テトラ「あ、確かにそうです。そういえばそうでした。加法定理なんですから、 $\alpha$ と $\beta$ の足し算を見つけるんでしたね。 先ほどの先輩のお話で」

僕「そうだね。いまちょうど $\alpha$ と $\beta$ という二つの角度の和がでてきたわけだ」

テトラ「はい。それで……？」

僕「うん、それでね、いま $\sin (\alpha + \beta)$ は見つかったから、 今度は $\sin \alpha \cos \beta + \cos \alpha \sin \beta$ を見つけたい。 そしてその両方が等しいといいたい。それが僕たちの目標だよ」

テトラ「なるほどです！　問題を《図形の世界》に移して考えようということですね！」

僕「そうなるね。そしていまはちょうど $\sin (\alpha + \beta)$ を見つけたところ」

テトラ「で、でも……《図形の世界》に移したとしても、 こんな複雑な式はあたしには見つけられません！」

ポリヤの問いかけ

僕「うん、そうだなあ……ねえ、テトラちゃん。 このあいだミルカさんが言ってたよね。 ポリヤの『いかにして問題をとくか』の話」

テトラ「はい？　あ、はい。《問いかけ上手なポリヤさん》ですね」

僕「うん。そのポリヤには《与えられた問題が解けなかったときの問いかけ》というのがある。 いくつかあるんだけど、その一つが——《問題の一部分を解くことはできるか》という問いかけだね」

テトラ「問題の一部分を解く……えっと、 $\sin \alpha \, \cos \beta + \cos \alpha \, \sin \beta$ の一部分って、 いったん何のことでしょう？」