![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/丸い三角関数』として書籍化されています。
僕とテトラちゃんは図書館で数学トークを続けている。 《点を回転する》ということを数学でどう扱うか、僕の説明が始まる。
僕「じゃ、点の回転について話すね。 いまは回転の中心を原点に固定しておくことにする。 その上で、座標平面上の点 $(a, b)$ を回転させよう」
座標平面上の点 $(a, b)$

テトラ「はい」
僕「点 $(a, b)$ を $30^\circ$ 回転させるとどこに来るだろうか。 回転の向きは左回り——つまり時計の逆回りだよ」
テトラ「このへんでしょうか」
座標平面上の点 $(a, b)$ を原点中心に $30^\circ$ 回転
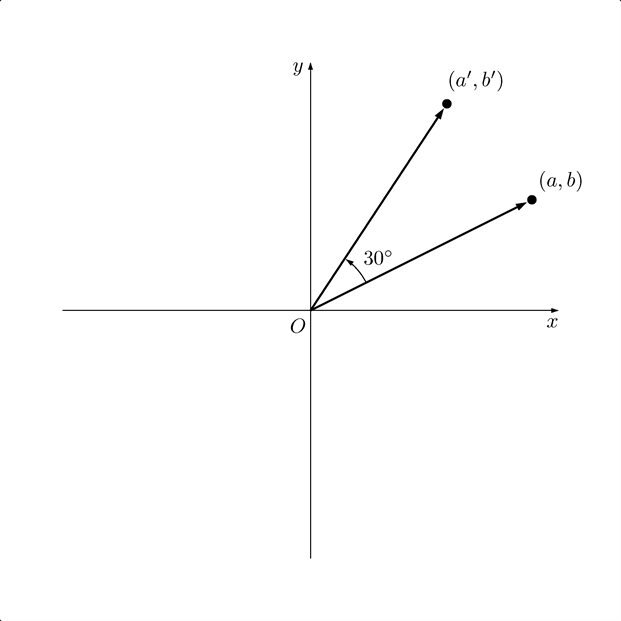
僕「そうだね。ちょうど原点にコンパスの針を置いて、円弧を描いたイメージだよね」
円弧を描く

テトラ「はい」
僕「僕たちはいま図を描いて《回転すると点はここに来る》と考えた」
テトラ「そうですね。この $(a,b)$ にあった点が……ぐうっと回ってこの $(a',b')$ に来ます」
僕「『これが、点を回転すること』といったら、なるほどって思うよね?」
テトラ「はい、そうですね。実際に回転してますし」
僕「ところで僕たちはいま点を $(a, b)$ のように表している。 $x$ 座標が $a$ で、 $y$ 座標が $b$ ということ」
テトラ「はい」
僕「そして、回転させた後の点を $(a', b')$ で表した。今度は $x$ 座標が $a'$ で、 $y$ 座標が $b'$ だね」
テトラ「はい、そうですね。回転したので座標がぐうっと変わったんですね」
僕「こんなふうに、点を $x$ 座標と $y$ 座標で表すとき《点を回転する》ってどういうことだと思う?」
テトラ「はい?」
僕「点を座標を考えているとき、何ができれば《点の回転ができる》といえるのか?と言い換えてもいいよ」
テトラ「なるほど……何ができればいいんでしょう」
僕「回転前の点は $(a,b)$ で、回転後の点は $(a',b')$ だ。だから《点を回転する》ことをこう考えよう」
《点を回転する》とは
回転前の点 $(a, b)$ の座標 $a$ と $b$ と回転の角度から、回転後の点 $(a', b')$ の座標 $a'$ と $b'$ を計算すること。
テトラ「ははあ……少しわかりました。 これは、 $a$ と $b$ を使って、何かこう……複雑な計算をして $a'$ と $b'$ を求めるということでしょうか」
僕「そうだね。複雑な計算かどうかは問題じゃないけど、そういうことだよ。 $a,b$ から $a',b'$ を計算して求める。それができれば、点の回転ができると見なせる。 実際には計算するための数式を作ることになる」
テトラ「はい、納得です……あ、いえ、ひとつ質問が」
僕「何?」
テトラ「$(a,b)$ から $(a',b')$ を計算するのはいいんですが、それは回転する前と回転した後という二つの点しか考えていないように 思うんです」
僕「うん、そうだね。それで?」
テトラ「あの……あたしは回転というと、先ほどコンパスで描いた円弧のようにぐうううっと動いている様子を想像しちゃうんです。 なので、二点しかないのに回転……というところに引っかかるんです」
僕「なるほど! うん、テトラちゃんの疑問はよくわかるよ。確かにそうだね。 回転というと動いている様子を考えたくなるかもしれないな。 でも、二点を考えるだけでも大丈夫だよ」
テトラ「どうしてですか?」
僕「いまから僕たちが考える点の回転——つまり座標の計算には、回転の角度が登場するからだよ」
テトラ「?」
僕「さっきは回転の角度は $30^\circ$ で考えたけど、 計算をするときには角度を $\theta$ という文字にして考える。 《文字の導入による一般化》をするということ」
テトラ「《文字の導入による一般化》……角度を $\theta$ として一般的に回転を考えるということですか」
テトラちゃんは、いつもの《秘密ノート》に書き込みながら言った。 テトラちゃんは、学んだ大事なことをぜんぶそこにメモしているんだ。
僕「そうそう。そうしておけば、 $\theta$ は好きな角度にできる。 $0^\circ$ でも $1^\circ$ でも $1.0000001^\circ$ でも、 $29.99999^\circ$ でもね。 さっきテトラちゃんが気にしていた円弧も描くことができる。 好きな角度に回転できるのは、コンパスを回せるということだね」
テトラ「ははあ、なるほどです。小さな角度の回転でも大きな角度の回転でも表せるという意味ですね」
僕「そうそう。僕たちはこれから、点を回転して《回転後の点を得る式》を作るんだけど、 二点を考えるだけで、円弧のことも考えていることになる。 角度を文字を使って一般的に扱うならね」
テトラ「わかりました……あ、でも、まだどういう式で点が回転するかはわかっていませんが」
僕「うん、じゃあ、回転の方法をいっしょに考えていこう」
テトラ「はいっ!」
僕「まずは考えようとしている僕たちの問題をもう一度整理する」
僕たちの問題:点 $(a,b)$ を回転しよう
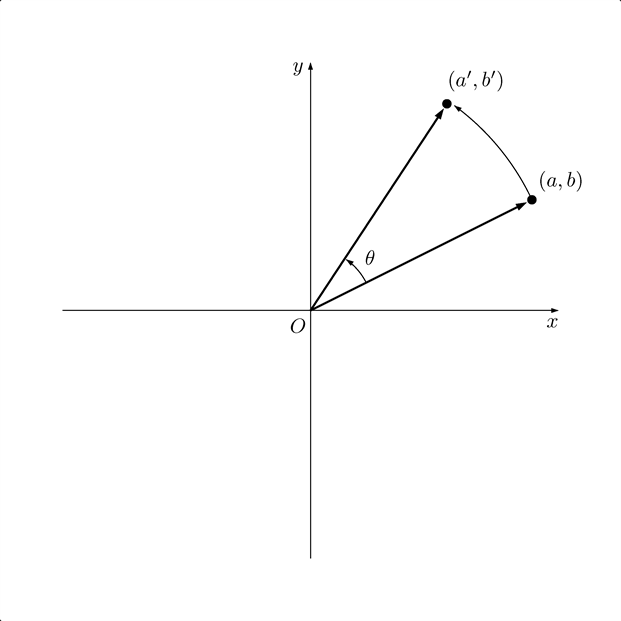
テトラ「はい、あたしたちの問題はわかりました……けれど、どうやって考えたらいいか、さっぱりわかりません。すみません」
僕「うん。やったことないと、さっぱりわからなくて当然だと思うよ。だから何もあやまらなくていいんだよ、テトラちゃん」
テトラ「教えていただけますか?」
僕「教えるのもいいんだけど、せっかくだから、数学でどう考えたらいいかわからないとき、僕がやることをいっしょにやってみようよ」
テトラ「え! 先輩が考えるみちすじってことですよね! はい! ぜひ!」
僕「といってもあたりまえのことなんだけどね。いま僕たちは、点 $(a,b)$ を回転するというとても一般的な問題を解こうとしていた」
テトラ「はい、《文字の導入による一般化》……ですよね」
テトラちゃんは、《秘密ノート》を見て言った。
僕「うん、一般的に考えるのはとても大事なんだけど、その分だけ抽象的になって解くのが難しいときもある。 そういうときには、わざと反対の方向に進んでみる。特殊化——まあ具体化といってもいいけど——をするんだ。《変数への代入による特殊化》だよ」
テトラ「?」
僕「一般的な点 $(a,b)$ を回転しようと考えるんじゃなく、たとえば、 $x$ 軸上にある点を回転しよう……とそんなふうに考えるんだ。 $x$ 軸上にある点に限定して考えるんだよ」
テトラ「$x$ 軸上にある点の回転……それが《変数への代入による特殊化》になるんですか」
僕「そうだよ。《$x$ 軸上にある》ということは《$y$ 座標の値が $0$》ってことだから、点 $(a,b)$ の $b$ に $0$ を代入した点 $(a,0)$ を 考えることになるよね。それで少し考えやすくなるかもしれない」
テトラ「ははあ、なるほどです!」
僕「だから、こんな $x$ 軸の問題1を考えてみよう」
$x$ 軸の問題1: $x$ 軸上の点 $(a,0)$ を回転しよう
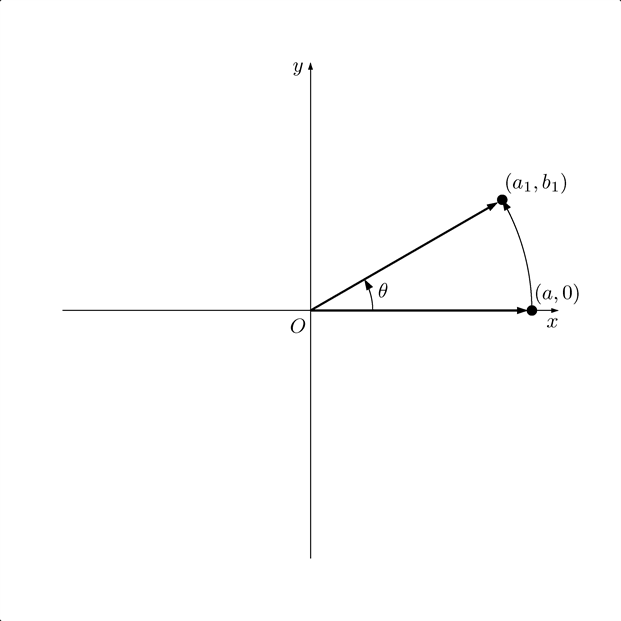
テトラ「あ、文字 $b$ がなくなりました」
僕「そうだね。文字を導入すると一般的になるけれど、文字を減らせば特殊になる。 それで問題が簡単になる場合もある」
テトラ「この $x$ 軸の問題1は……あたしにも解けるんでしょうか」
僕「まずは自分で図を描いてみようよ」
テトラ「あ、そうですね」
テトラちゃんの図、その一

テトラ「……はい、描けました」
僕「《求めるものは何か》」
テトラ「はい?」
僕「数学を考えるときの《問いかけ》だよ。この問題でテトラちゃんが《求めるものは何か》」
テトラ「求めるものは……はい、 $a_1$ と $b_1$ です」
僕「だったら、それも図に描かないと」
テトラ「あ、そ、そうですね。すみません」
テトラちゃんの図、その二

僕「さあ、どうかな。これで問題1は解けるかな」
テトラ「えっと……」
僕「それじゃ、次の《問いかけ》だよ。この問題でテトラちゃんが《与えられているものは何か》」
テトラ「与えられているものは……はい、 $a$ と $b$ ……あ、 $b$ はないですから、与えられているものは $a$ です」
僕「それだけ?」
テトラ「え……あ、違います。角度 $\theta$ もあります。与えられているものは $a$ と $\theta$ でした」
僕「そうだね。じゃあ、 $a$ と $\theta$ も図に描かないと」
テトラ「は、はい……そうか、そうなんですね」
僕「何が?」
テトラ「先輩の《問いかけ》です。 《求めるものは何か》と《与えられているものは何か》という問いかけです。 あたし、自分がぼんやりと問題を読んで、ぼんやりと図を描いているんだ……というのがよくわかりました」
僕「そう?」
テトラ「はい。 《求めるものは何か》と《与えられているものは何か》と自分に問いかけて、 きちんと思い出して、図を描く必要があるのですね」
僕「うん、そうだね」
テトラ「では図を描きます!」
テトラちゃんの図、その三
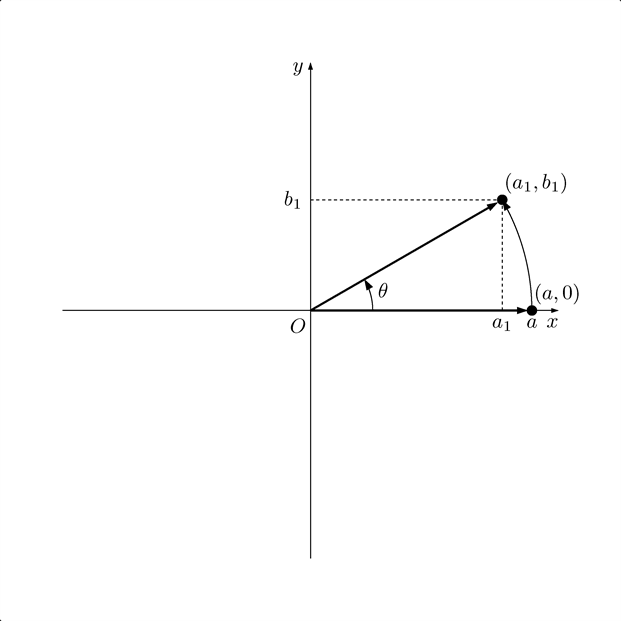
僕「じゃあ、問題の続きを考えよう」
テトラ「はい、そうですね」
僕「さあどうかな?」
テトラ「え、ええと……」
僕「もうちょっとなんだけどね……じゃあ、次の《問いかけ》だよ。《似ているものを知らないか》」
テトラ「似ているもの……ですか。い、いえ、わかりません」
僕「じゃあ、大ヒントになっちゃうけど、この図を見よう。ね、このあいだ見たこの図、似てない?」
単位円と $\cos \theta, \sin \theta$ との関係
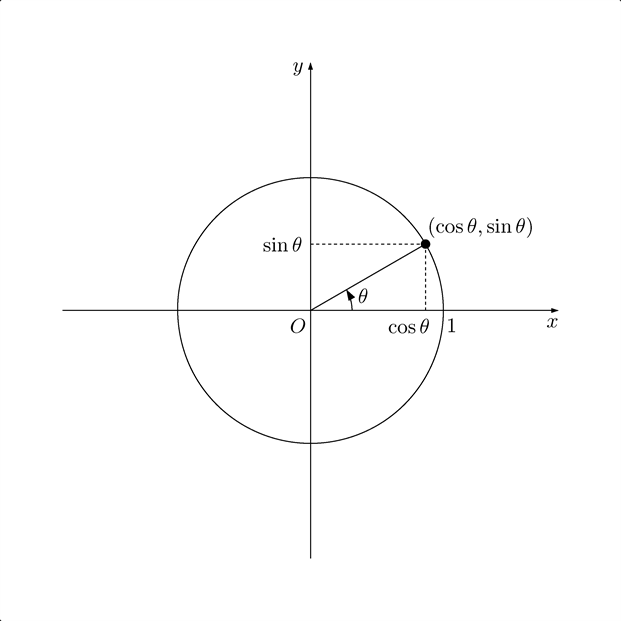
テトラ「あ……これはサインを——あの $\sin$ を教えていただいたときの図ですね」
僕「そう。テトラちゃんがいま問題1のために描いた図と似てない? 特に、こんなふうに大きな円を描いてみると……」

テトラ「ああああっ! 確かにそっくりですね! 左は単位円——半径が $1$ の円です」
僕「うん、で?」
テトラ「だから、えっと、右は半径が $a$ ですから、もしかして……」
僕「もしかして?」
テトラ「もしかして、 $a$ 倍すればいいんでしょうか? $x$ 座標も $y$ 座標も!」
僕「そうそう、それでいいんだよ。いまテトラちゃんが言ったこと、数式を使って書ける?」
テトラ「両方 $a$ 倍するんですから……こうですか?」
$$ \begin{align*} a_1 &= a \cos \theta \\ b_1 &= a \sin \theta \\ \end{align*} $$
僕「はい、大正解!」

テトラ「はわわ……そうですよね、 $a$ 倍するだけでよかったんですね」
僕「でも気が付かないときには気が付かないものだよね」
テトラ「そうですね」
僕「テトラちゃんが気づいた二つの式をよくよく見てごらん」
テトラ「はい?」
$$ \begin{align*} a_1 &= a \cos \theta \\ b_1 &= a \sin \theta \\ \end{align*} $$
僕「$\cos$ や $\sin$ が出てくるとややこしく見えるけれど、 $a_1$ と $b_1$ を、 $a$ と $\theta$ から求めているということを確かめないとね」
テトラ「あ、《求めるものは何か》ですね!」
僕「そうそう」
テトラ「確かにそうですね。求めるもの——つまり $a_1$ と $b_1$ を、 与えられているもの——つまり $a$ と $\theta$ で求めています。確かに!」
$$ \begin{align*} a_1 &= a \cos \theta \\ b_1 &= a \sin \theta \\ \end{align*} $$
僕「そうだね」
テトラ「あの……念のための確認ですけれど、あたしはさきほど $a \cos \theta$ や $a \sin \theta$ と書きましたが、 これでいいですよね」
僕「うん、いいけど?」
テトラ「あたしは $a \cos \theta$ を、 $a$ と $\cos(\theta)$ の掛け算のつもりで書いたんです」
僕「うんうん、それでいいよ」
$$ \begin{align*} a \cos \theta & = a \times \cos(\theta) \\ a \sin \theta & = a \times \sin(\theta) \\ \end{align*} $$テトラ「はい、安心しました」
僕「うん。さあテトラちゃん。ここまでで、 $x$ 軸の問題1は解けたね」
$x$ 軸の問題1: $x$ 軸上の点 $(a,0)$ を回転しよう
$x$ 軸の問題1の解答
$$ \begin{align*} a_1 &= a \cos \theta \\ b_1 &= a \sin \theta \\ \end{align*} $$
テトラ「……先輩、あの、いま問題1をとくとき、ほとんど先輩に教えていただいたんですが、 でも、なんだか、変なんです」
僕「何が?」
テトラ「なんだか、あたし、自分で考えたみたいな気持ちなんです」
僕「そう?」
テトラ「はい、そうです。ヒントもたくさん出していただいたんですが、 何だか自分の頭の中で、 $\cos \theta$ と $\sin \theta$ がうまく思い描けたような……」
僕「それじゃね、今度はほんとに自分で考えてみない? $y$ 軸の問題2だよ」
テトラ「え?」
$y$ 軸の問題2: $y$ 軸上の点 $(0,b)$ を回転しよう
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2013年4月26日)
この記事は『数学ガールの秘密ノート/丸い三角関数』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!