第25回 シーズン3 エピソード5

世界を回す（前編）

図書室にて

テトラ「先輩！　数学をなさっているんですか？」

僕「そうだよ、テトラちゃん」

テトラちゃんはいつも元気いっぱいな女の子。 数学はそれほど得意じゃないけれど、とても熱心に勉強している。 僕が書いていたノートを興味深そうに見ている。

テトラ「これは……？」

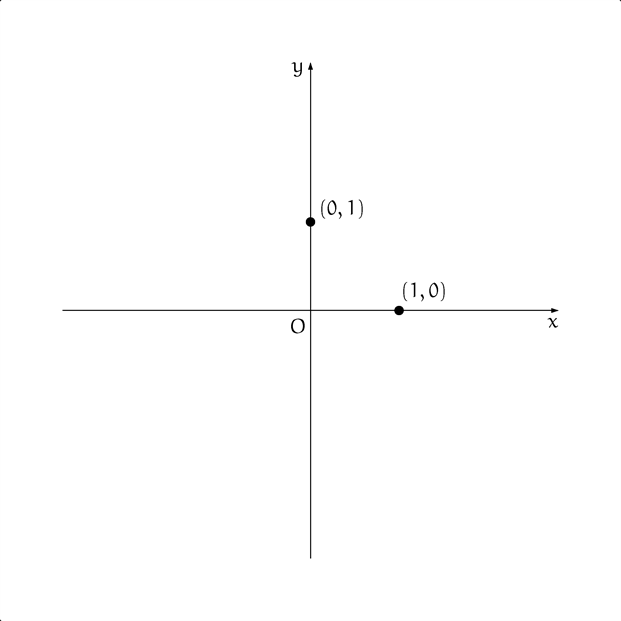
僕「見ての通り、座標平面だよ」

テトラ「はい……でも、何も描かれていませんね」

僕「うん、ちょっと考えごとしていたんだ。でも何も描いてないわけじゃないよ。ほらここに二つの点があるよね。 $(1,0)$ と $(0,1)$ だ」

テトラ「はい」

僕「$x$ 軸上に $(1,0)$ で、 $y$ 軸上に $(0,1)$ がある。この二つの点はとても大切なんだよ。この二つの点を使えば、世界が作れるからね」

テトラ「世界！　そんなものが作れるんですか！」

僕「ごめん……いま言った世界というのは、えっとね、この平面の上のことだよ」

テトラ「はあ……」

テトラちゃんはきょとんとした顔で、大きな目をぱちぱちさせた。

僕「ねえ、テトラちゃん。テトラちゃんは、《図形は点の集まりである》という言葉の意味はわかる？」

テトラ「はい？　……え、ええ、わかると思います。 図形というのは三角形や四角形や直線や……そういうもののことですよね？　そういう図形はどれも点が集まってできてます」

僕「そうだね。 この座標平面上に描かれる図形はぜんぶ点の集まりだ。数学では《点の集合》といったりする」

テトラ「はい」

僕「数学では図形を扱うことがよくあるよね。 図形は《点の集合》なんだから、 点をうまく扱うことができれば、 それは図形をうまく扱うことにつながっていく——というのはわかる？」

テトラ「は、はい。 おっしゃることはわかりそうです。一つ一つの点をうまく扱えれば、 点が集まった図形もうまく扱えるってことですよね。 具体的にその《数学で点を扱う》って何なのか、よくわかりませんが……」

僕「たとえば、以前いっしょに放物線のグラフを描いたじゃない？　グラフは数学で扱う図形の代表選手だね。 あのときも、グラフという図形を点の集まりとして考えた」

テトラ「えっと——確か、図形の方程式が出てきました」

僕「そうだね。 $y = x^2$ という放物線の方程式があると、その放物線の上にあるということで点には制約がかかる」

テトラ「はい、ルールで縛られるんですね。放物線の上に乗ってなくちゃいけないので」

僕「そうそう。放物線上の点——ほら、点だ！——を $(x, y)$ としたとき、 その点は必ず $y = x^2$ という関係式を満たす」

テトラ「そうでしたそうでした。それが図形の方程式、ですよね」

僕「うん、そこで……そこで、また話は座標平面に戻る。この平面上にはたくさんの点——無数の点があるよね。 この図では $(1,0)$ と $(0,1)$ という二点しか描いていないけど」

テトラ「はい、わかります。この平面をびっしりと敷き詰めるように点がある——はずです。見えませんけど」

僕「座標平面にある点はすべて二つの数のペアで表せる。 $(a, b)$ のように書いて、 $x$ 座標が $a$ で、 $y$ 座標が $b$ になる二つの数のペア」

テトラ「はい！　授業では《将棋盤や碁盤のよう》と習いました」

僕「ああ、そうだね。二つの数のペアで一つの点を表している。 ところで、 $(a, b)$ という書き方についてもう少し深く考えてみよう」

テトラ「はい」

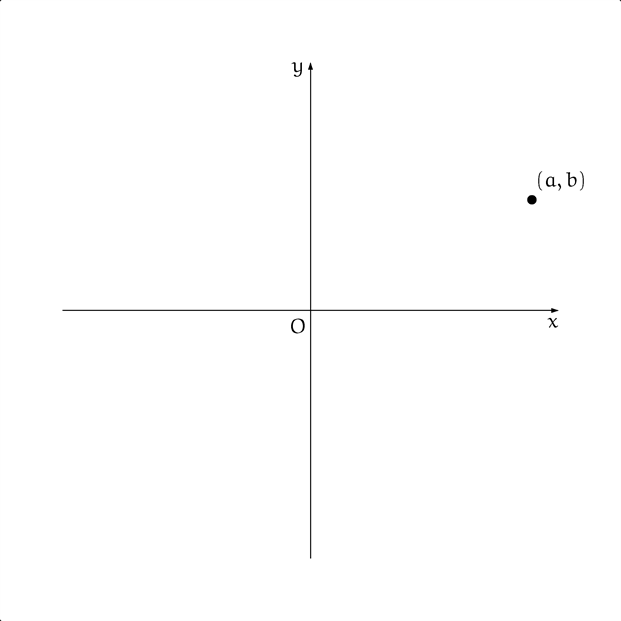
僕「適当に選んだ点 $(a, b)$ がたとえばここにあるとしよう」

テトラ「はい」

僕「理解の確認だけど、この点 $(a, b)$ の《$x$ 座標》と《$y$ 座標》はわかる？」

テトラ「え？　あ、はい、わかります。この点の $x$ 座標は $a$ で、 $y$ 座標は $b$ ですね。 ここにこう……点線を書いて、はい」

僕「うん、それでいい。 $a$ のことを点 $(a, b)$ の $x$ 成分と呼ぶこともある。 $b$ は点 $(a, b)$ の $y$ 成分」

テトラ「成分……なんだか化学みたいですね」

僕「そうだね。成分という言い方をするのは、 $a$ と $b$ が $(a, b)$ を作るモトになっているからだと思うな」

テトラ「はい、なるほどです」

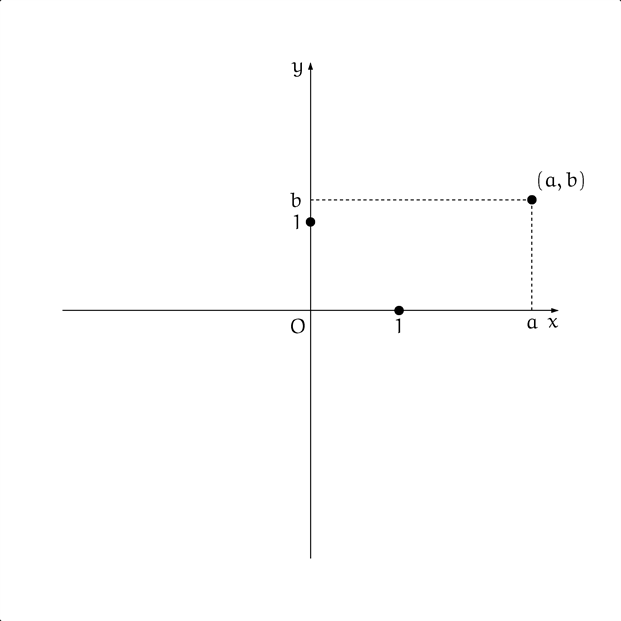
僕「いまは $a$ と $b$ のように簡単に書いたけれど、 その $a$ と $b$ という数の意味をきちんととらえるためには、 $x$ 方向と $y$ 方向のそれぞれの単位がわかっていなくちゃいけない。 言い換えると $x$ 方向と $y$ 方向のそれぞれの $1$ の大きさを確認しなくちゃいけない。 それがさっきから僕がいってるこの $2$ 点なんだよ」

テトラ「え……何をおっしゃっているのか、よくわからなくなりました」

僕「たとえば、この点 $(a, b)$ に行くには、 原点 $(0,0)$ から右方向に $a$ だけ進み、上方向に $b$ だけ進めばいいよね」

テトラ「そうですね」

僕「それで場所が決まる！　…というためには《$a$ だけ進むというのがどれだけの大きさか》をわかっていなくちゃね」

テトラ「基準になる量が必要ということでしょうか」

僕「そうそう。その基準となる量のことをいま単位と呼んだんだよ」

テトラ「はい……何とかわかりました」

僕「右方向、つまり $x$ が大きくなるときの $1$ と、 上方向、つまり $y$ が大きくなるときの $1$ がはっきりすれば、座標平面上のどんな点でも、 $(a, b)$ という数のペアで表せることがはっきりする。 そのときの $a$ は $x$ が原点 $(0,0)$ からどれだけ右に進んだか、 $1$ 単位の何倍右に行ったかを定めているし、 そのときの $b$ は $y$ が原点 $(0,0)$ からどれだけ上に進んだか、 $1$ 単位の何倍上に行ったかを定めている」

テトラ「はい、よくわかります。 碁盤の目のような平面を右に $a$ だけ、上に $b$ だけ進んだところに $(a, b)$ という点があるということですよね？」

僕「それでいいよ。こんなふうにマス目を描くとイメージしやすい」

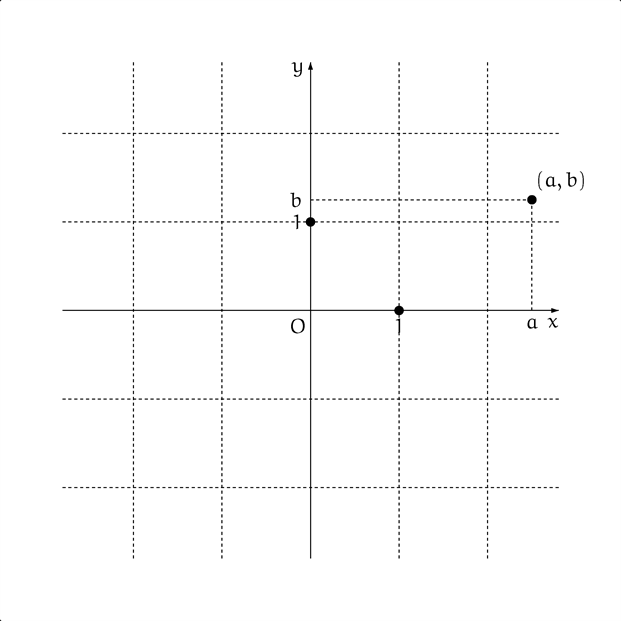
テトラ「あ、そうですね。右方向（$a$）は $2$ と少し、上方向（$b$）は $1$ と少しです」

ベクトル

僕「ここまでは座標平面の復習だね。 ここから、ベクトルというものについて話してみよう。授業でベクトルは習った？」

テトラ「は、はい……いちおう習いました。 あの、矢印が出てくるんですが、正直まだ《わかった感じ》はしていないです」

僕「実はね、ベクトルの基本的なところは、いままで話したことでもう説明は済んでいるんだよ」

テトラ「え！　でも、矢印が出てきてませんが……」

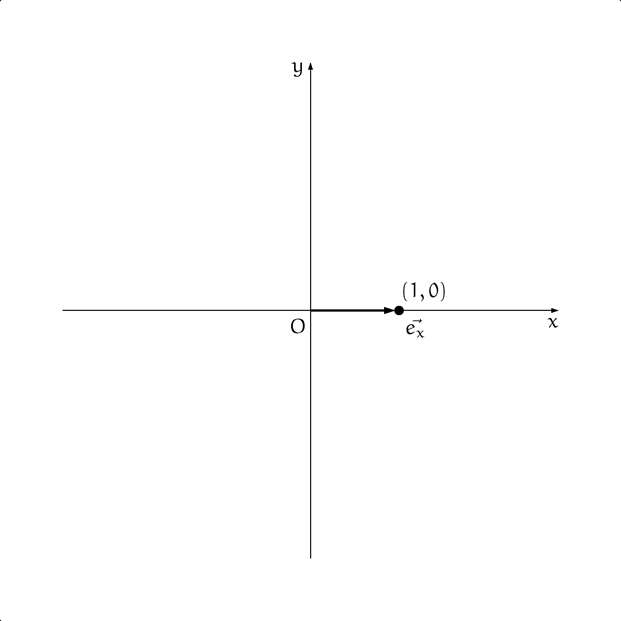
僕「そうだね。たとえば、点 $(1,0)$ と点 $(0,1)$ が大事だよという話をしたけど、 その話は、こういう二つの単位ベクトルの話をしていた——ともいえる」

点 $(1, 0)$ と単位ベクトル $\vec{e}_x$

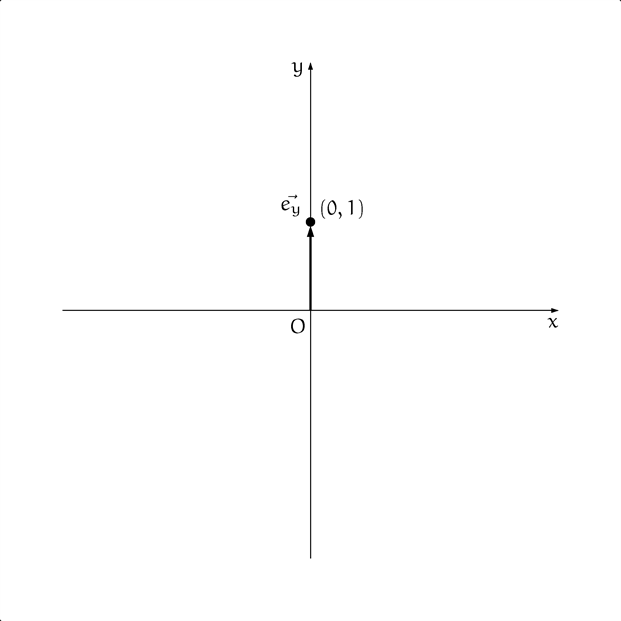
点 $(0, 1)$ と単位ベクトル $\vec{e}_y$

テトラ「え……ええと。確かに矢印は出てきましたが……」

僕「ベクトルはよく矢印で表す。矢印は始まりの点（始点）と終わりの点（終点）の二点で決まるよね」

テトラ「そうですね。終わりの点というのは矢印の先のことですね？」

僕「そうだね。矢印が二点で決まるというのなら、始点を原点 $(0,0)$ に固定してしまえば、 矢印というのは点と同じことだよね。終点が決まれば矢印も決まるから」

テトラ「ははあ……それはそうですが」

僕「いまは点 $(1,0)$ をベクトル $\vec{e}_x$ で表して、 点 $(0,1)$ をベクトル $\vec{e}_y$ で表した。 そうやって、ベクトルと点とを同一視することができる。同じものと見なすことができるということ」

テトラ「ベクトルと点とを同じものと見なす……」

僕「この図を見てごらん」

テトラ「はい」

点 $(a,b)$ とベクトル $\vec{v}$

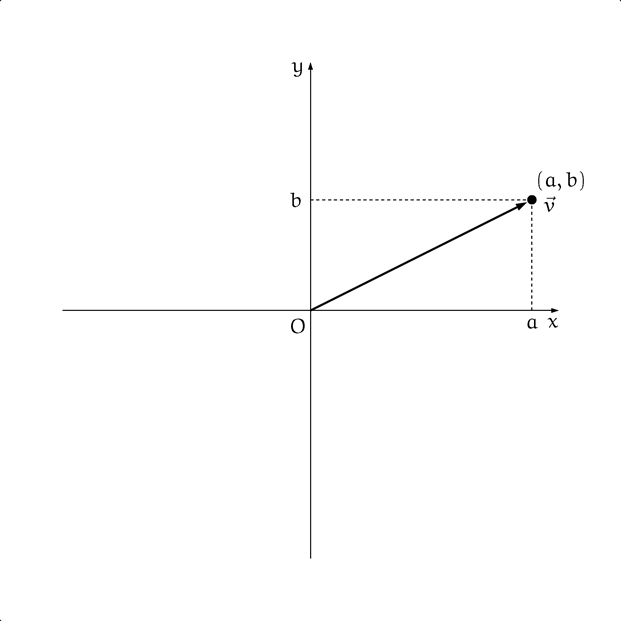
僕「このベクトル $\vec{v}$ と、点 $(a,b)$ とを同一視するということだね」

テトラ「先輩、すみません……難しすぎてわかりません」

僕「いやいやいや、いまは難しい話をしているわけじゃないよ」

テトラ「でも、どうしてこのベクトル $\vec{v}$ が $(a,b)$ という点と同一視できるのか、 その理論……というんでしょうか、それがあたしにはわからないんです！」

僕「うん、ええとね、テトラちゃん。 いまは何か深遠な理論を使って何かを導いたり証明しているわけじゃない。 そうじゃなくて、これは《ものの見方》の話をしているんだ」

テトラ「……」

僕「そうだなあ……テトラちゃんにピンと来る言い方をするなら、 いま説明しているのは、ベクトルという《平面上の点を表現する方法》について話しているんだ。表現方法の一つ、だね」

テトラ「表現する方法……コトバってことですか！」

僕「そうだね。そう考えてもいいよ。僕たちは平面上の点を表現する方法を二つ話してきた」

• 描画：方眼紙の上に具体的に描いて点を表す方法。
• 成分：座標軸を定めて、 $(a,b)$ のように $x$ 座標と $y$ 座標の二つの数のペアで点を表す方法。

テトラ「はい、そうでした」

僕「そしてね、いま話していたのは、点を表すもう一つの方法」

• ベクトル：原点に始点を持つ矢印の終点で点を表す方法。

テトラ「あ……え……それだけのことなんですか」

僕「そうだよ。それだけのこと。もちろん、厳密な話をすれば、 そんなふうに矢印を使って点を表すということの妥当性について議論が必要になるだろうけれどね。 ともかく、いまは、ベクトルという表現方法を使って点を表すことができるよ、 それはこんなふうに矢印で表すことが多いよ——というだけのことなんだ」

テトラ「あたし……何だか《ベクトル》という難しそうな言葉のために難しく考えてしまってました。 要するに点の表現方法だと思っていてもいいでしょうか」

僕「うん、いいよ。 ベクトルの役割はいろいろあるけれど、点を表現するのもその一つになるよ。 厳密には《位置ベクトル》といったりする」

テトラ「そうなんですね……」

僕「数学では考え方そのものはとてもシンプルなんだけど、 厳密に表現するために新しい言葉を使うことがあるよね。 そのために、初めて出会う言葉にとまどっちゃうんだ」

テトラ「まさにそうです！　難しそうな言葉でうわわわってなっちゃって……」

僕「本を読んだり、授業を聞いたりするときも、そこでぐっとこらえて、 言葉の難しさではなくて、説明されている内容に集中した方が良いよ」

テトラ「わかりました」

ベクトルを伸ばす（ベクトルの実数倍）

僕「ベクトルは点と同一視できるんだけど、ベクトルならではの計算もある。ベクトルの計算だね」

テトラ「ベクトルの計算？」

僕「そう。たとえば、ベクトルの向きを変えずにするするっと伸ばす計算がある。 それは実数をベクトルに掛ければいい。 実数 $a$ を単位ベクトル $\vec{e}_x$ に掛けると、ベクトルは $a$ の大きさに応じて伸びる。 これをベクトルの実数倍というよ。図でイメージするとこんな感じ」

ベクトルを伸ばす（実数 $a$ を単位ベクトル $\vec{e}_x$ に掛けた様子）

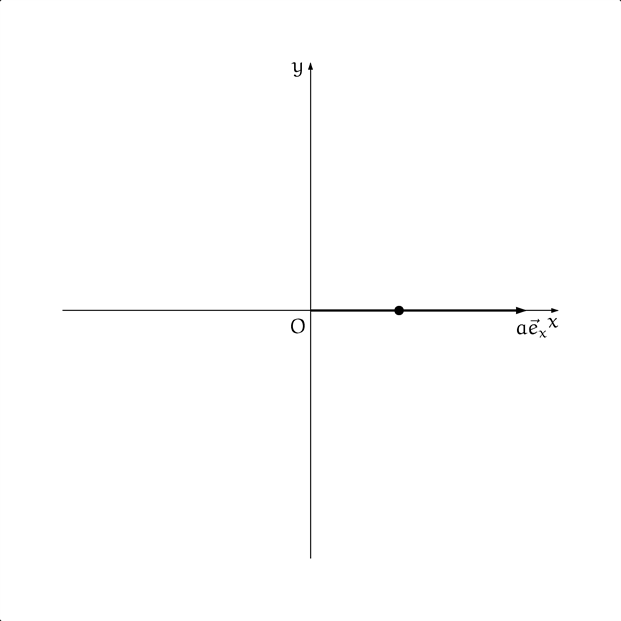
テトラ「はい、イメージできました。ベクトルを伸ばす」

僕「たとえば実数 $b$ を単位ベクトル $\vec{e}_y$ に掛けたらこうなる」

ベクトルを伸ばす（実数 $b$ を単位ベクトル $\vec{e}_y$ に掛けた様子）

テトラ「はいはい、ちょっぴり伸びました」

ベクトルを足す

僕「それからもう一つベクトルの計算があるよ。 さっきは実数をベクトルに掛けた。今度はベクトル同士の足し算だね。たとえばさっき作った二つのベクトルを加えると、 新たなベクトル $\vec{v}$ が作れる」

ベクトルを足す（ベクトル $a\vec{e}_x$ とベクトル $b\vec{e}_y$ とを足した様子）

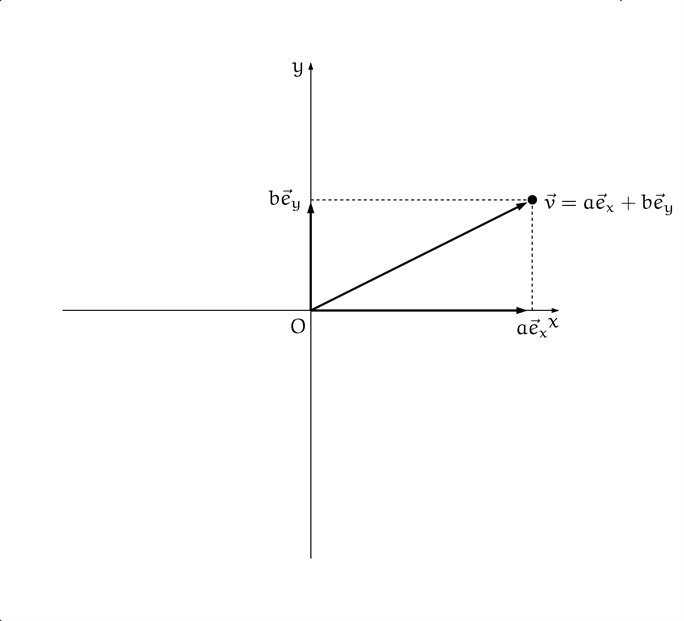
テトラ「あ！　これ授業でやりました！　先生のお話は理解できたんですが、《だから、何？》と思ったところです」

僕「うん、そうだね。ベクトルの足し算は、描いた図形を見ると何となく《まあそうかな》と思えるんだけど、 《だから、何？》って思っちゃうかもね。でも、さっきの《ベクトルの実数倍》と《ベクトルの足し算》という武器を手に入れてみると、 気がつくことがある」

テトラ「気がつくこと……といいますと？」

僕「ほら、三種類の点の表現方法について話したよね。 《図形として点を表現する》 《$(x,y)$ の成分で点を表現する》 それから《ベクトルとして点を表現する》……」

テトラ「はい？」

僕「図形として点を表現すると、僕たちは点を目で見ることができる。 $(x,y)$ の成分で点を表現すると、僕たちはヨコにどれだけタテにどれだけ動けばその点にたどり着けるかがわかる」

テトラ「はい、そうでした」

僕「そして、ベクトルとして点を表現すると、僕たちは点を使って《計算》ができるようになったわけだ！」

テトラ「あ……」

僕「そうなんだよ。もちろん、成分を使っても計算はできる。 でもベクトルとして点を表現すると、成分を忘れて計算することもできる。 そのときに使えるのがこの《ベクトルの実数倍》と《ベクトルの足し算》という二つなんだ」

テトラ「あ……あたし、まだわかってないんですけど、何か、ちょっとわかりました。ベクトルについて！」

回転

僕「それで、と。僕がさっき考えていたのは……回転のことなんだ」

テトラ「回転？　ぐるぐる何回も回るあの回転ですか？」

僕「そう。回転。でも数学でいう回転は、何回も回らなくてもいいんだよ。 回転には回転の中心と回転角があればよくて、回転角はほんの少しでもいい」

テトラ「回転角——それは、どれだけ回すかの角度のことですね」

僕「そうだね。回転では回転の中心と回転角の二つが大切なんだけど、 いまは回転の中心を原点に固定しておくことにする。 その上で、座標平面上の点 $(a, b)$ を回転させたい」

テトラ「なぜですか？」

僕「えっ？」

テトラ「なぜ、点を回転させたいんですか？」

テトラちゃんの質問に僕は一瞬絶句した。