![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/丸い三角関数』として書籍化されています。
僕「……こんなふうにタテ線とヨコ線をずらして始めると楕円になったね」

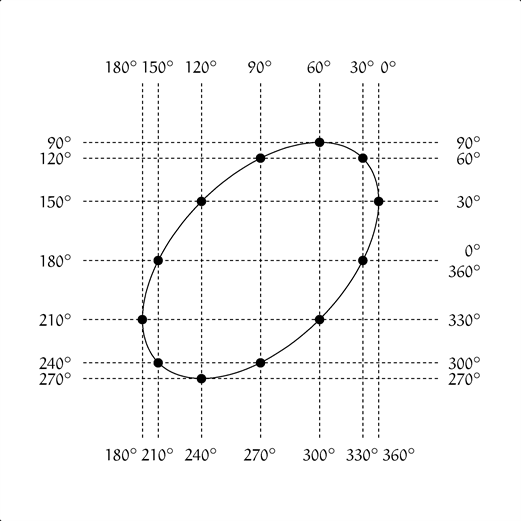
ユーリ「おもしろーい」
僕「この図形は全部、ユーリがさっき言ってた $49$ 個の点だけを使って作られているんだ」
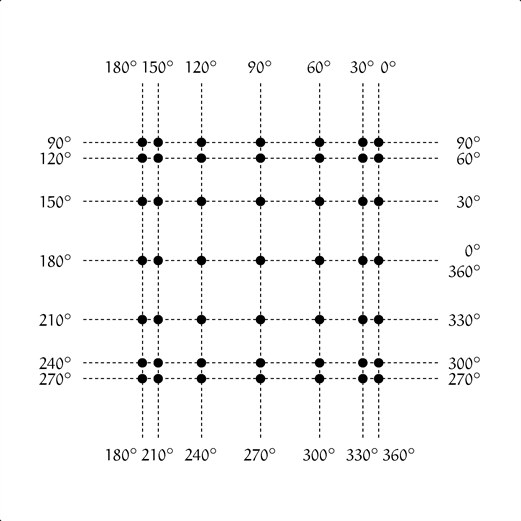
ユーリ「おーっ! 確かに!」
僕「今度は、別の図形を作ってみよう」
ユーリ「別の図形?」
僕「うん。そうだなあ……さっきはタテとヨコを同じ角度ずつ動かしたよね」
ユーリ「うん。 $30^\circ$ っしょ?」
僕「そうだね。今度は、タテを $30^\circ$ 動かすごとにヨコを $60^\circ$ 動かしてみよう」
ユーリ「二倍大きく動かすってこと? おっきな楕円ができるだけじゃないの?」
僕「いやいや、半径を変えるわけじゃない。角度を二倍大きく動かすんだから、円や楕円の大きさが大きくなるわけじゃないよ」
ユーリ「あ、そっか。角度が $60^\circ$ ごと動いても、 この $49$ 個の点よりも外に動くわけじゃないのか。でも……そーぞーつかないにゃあ」
僕「楕円を作ったときは、タテ線とヨコ線をひと目盛りずつ動かしていったよね」
ユーリ「うん、そうだった」
僕「端までいったら反射した」
ユーリ「うんうん。跳ね返るってことっしょ?」
僕「今度はね、《タテ線をひと目盛り左右に動かす》ごとに《ヨコ線はふた目盛り上下に動かす》。 そのときタテ線とヨコ線の交点が作る図形はどういう図形になるか……それがクイズ」
ユーリ「おもしろそー……だけど、むずかしそー……」
僕「じゃあ、実際にやってみようか」
ユーリ「待って待って待って! ユーリ、頭だけで考えてみたい!」
僕「いいよ。じゃあちょっと待つね」
ユーリが深い思考モードに入った。 栗色のポニーテールが美しい金色になる。 彼女はいつもはとってもめんどくさがりだけど、 興味を持つと急激に頭が回転する。 しかも論理的に考える力がとっても強い。 本人はあまり自覚していないようだけど……
ユーリ「……やっぱ、わかんにゃい!」
僕「じゃあ、実際に描いてみよう」
ユーリ「うん! でも、わかったことがあるよ」
僕「何?」
ユーリ「あのね、タテ線を $30^\circ$ 動かすごとにヨコ線を $60^\circ$ 動かすんだよね?」
僕「そうだけど?」
ユーリ「だったらさ、タテ線がぐるっと一回転したら、ヨコ線は二回転するよね?」
僕「おお、確かにそうだね」
ユーリ「回転……ってゆーのは変だにゃ。回転するのは円周上の点で、タテ線とヨコ線は……こう……行ったり来たり?」
僕「うん、ユーリはよくわかっているね。タテ線が一往復したらヨコ線は二往復するんだね」
タテ線が一往復

ヨコ線は二往復

ユーリ「おーふく。うん、そーゆーこと」
僕「じゃあ、実際に描いてみよう」
ユーリ「わくわくぅ!」
僕「まず、スタート地点を確認しよう。単位円の円周上、角度が $0^\circ$ の地点からスタートする。 タテ線とヨコ線の両方に $0^\circ$ と印を付けておく」
ユーリ「いーよ」
$(x, y) = (\cos 0^\circ, \sin 0^\circ)$

僕「次の一歩。タテ線を左にひと目盛り動かして、 ヨコ線は上にふた目盛り動かす。 タテ線は角度が $30^\circ$ の場所だけど、 ヨコ線は角度が $60^\circ$ の場所になる」
$(x, y) = (\cos 30^\circ, \sin 60^\circ)$
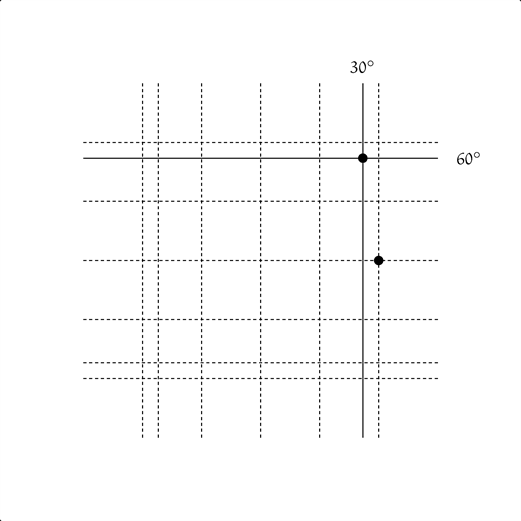
ユーリ「うん。これは想像付いたよ。大きくナナメジャンプするんだ。でも次がよくわかんなくなっちゃったの」
僕「そう? 次の一歩は、タテ線を左にひと目盛り動かして、 ヨコ線はふた目盛り動かす。でもここで注意が必要。 ヨコ線は角度が $60^\circ$ の場所から $60^\circ$ 動かすんだから、 $120^\circ$ の場所まで来る。つまり、ヨコ線はふた目盛り動いた結果、 上で反射して、同じ場所になるんだ」
ユーリ「あ!」
僕「だから、タテ線は角度が $60^\circ$ の場所で、 ヨコ線は角度が $120^\circ$ の場所になる——動かないんだけどね」
$(x, y) = (\cos 60^\circ, \sin 120^\circ)$
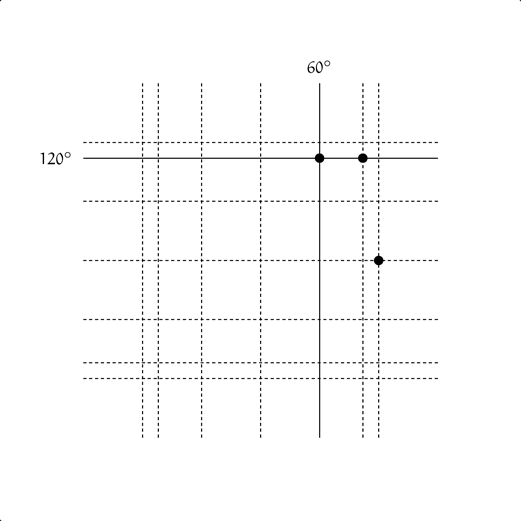
ユーリ「そっかー。上で反射して……そっかー」
僕「まだ形はよくわからないよね」
ユーリ「うん……」
僕「次の一歩は、タテ線は相変わらず $30^\circ$ 進んで $90^\circ$ になる。 ヨコ線は、 $60^\circ$ 進んで $180^\circ$ になるね」
$(x, y) = (\cos 90^\circ, \sin 180^\circ)$
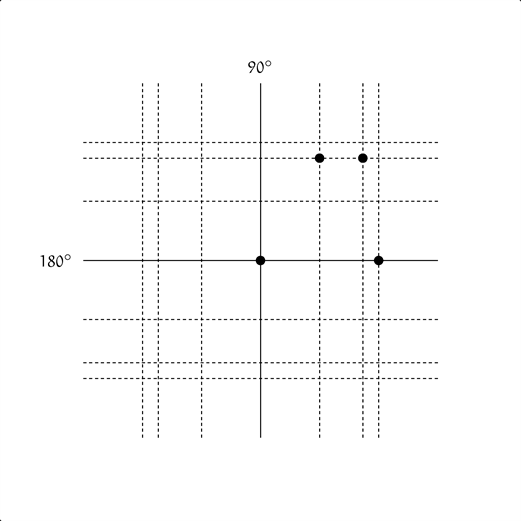
ユーリ「あ! 見えてきた! やっぱ、楕円じゃない? 細長い楕円だよ」
僕「そうかな?」
ユーリ「……あんま自信ない」
僕「次の一歩は、タテ線は $120^\circ$ で、 ヨコ線は、 $240^\circ$ だね」
$(x, y) = (\cos 120^\circ, \sin 240^\circ)$
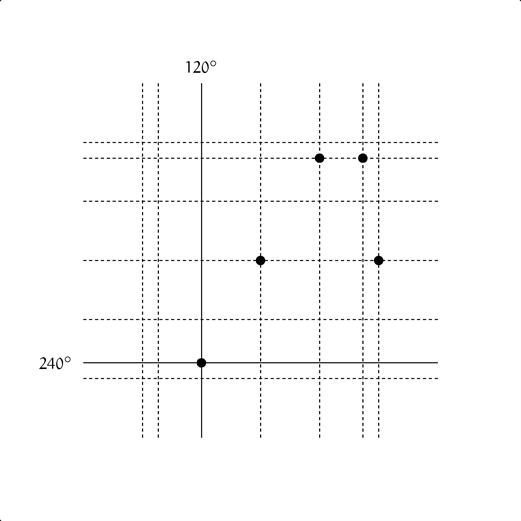
ユーリ「ありゃ? これじゃ、細長い楕円が下に突き抜けそうだよ」
僕「いやいや、ユーリ。楕円の発想から離れよう。対称性を考えたら、次にどうなるかは想像が付くはずだよ」
ユーリ「対称性?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2013年4月12日)
この記事は『数学ガールの秘密ノート/丸い三角関数』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!