![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/丸い三角関数』として書籍化されています。
ユーリ「お兄ちゃん、これ何?」
ユーリは、僕がそのへんに放り出していたルーズリーフを持ってきた。 彼女は中学二年生、僕の従妹だ。 でも僕のことをいつも《お兄ちゃん》と呼ぶ。
僕「ん? この図のこと?」



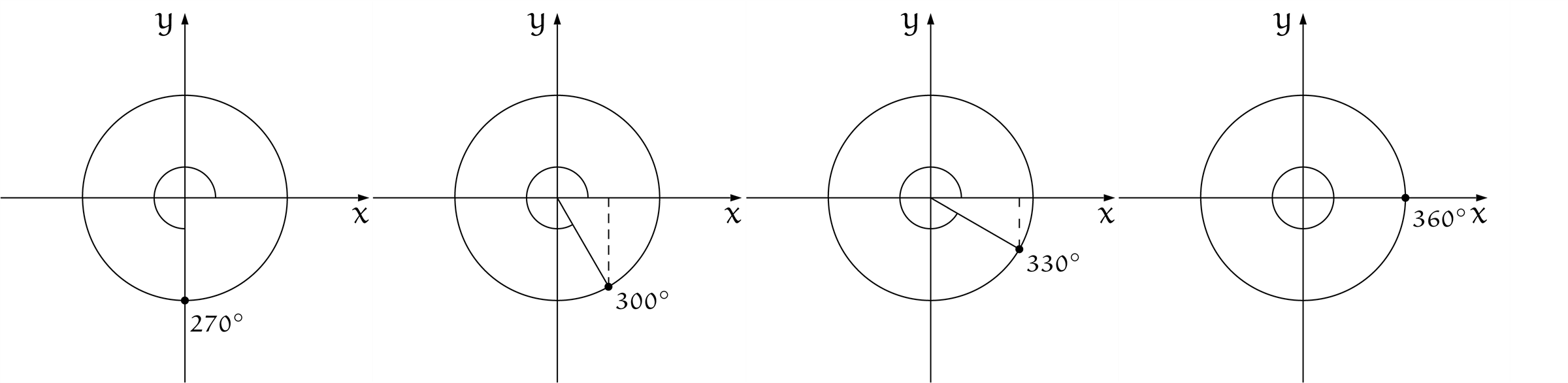
ユーリ「なんか、おもしろそーじゃん」
僕「おもしろいよ。これは単位円を使って……」
ユーリ「たんいえん?」
僕「単位円っていうのは半径が $1$ の円のことだよ」
ユーリ「ふーん……」
僕「まず、単位円の円周上に点を置く。それからその点をぐるっと回していくんだよ。こんなふうに、 $30^\circ$ ずつね」
単位円の円周上、点を $30^\circ$ ずつ回転させる
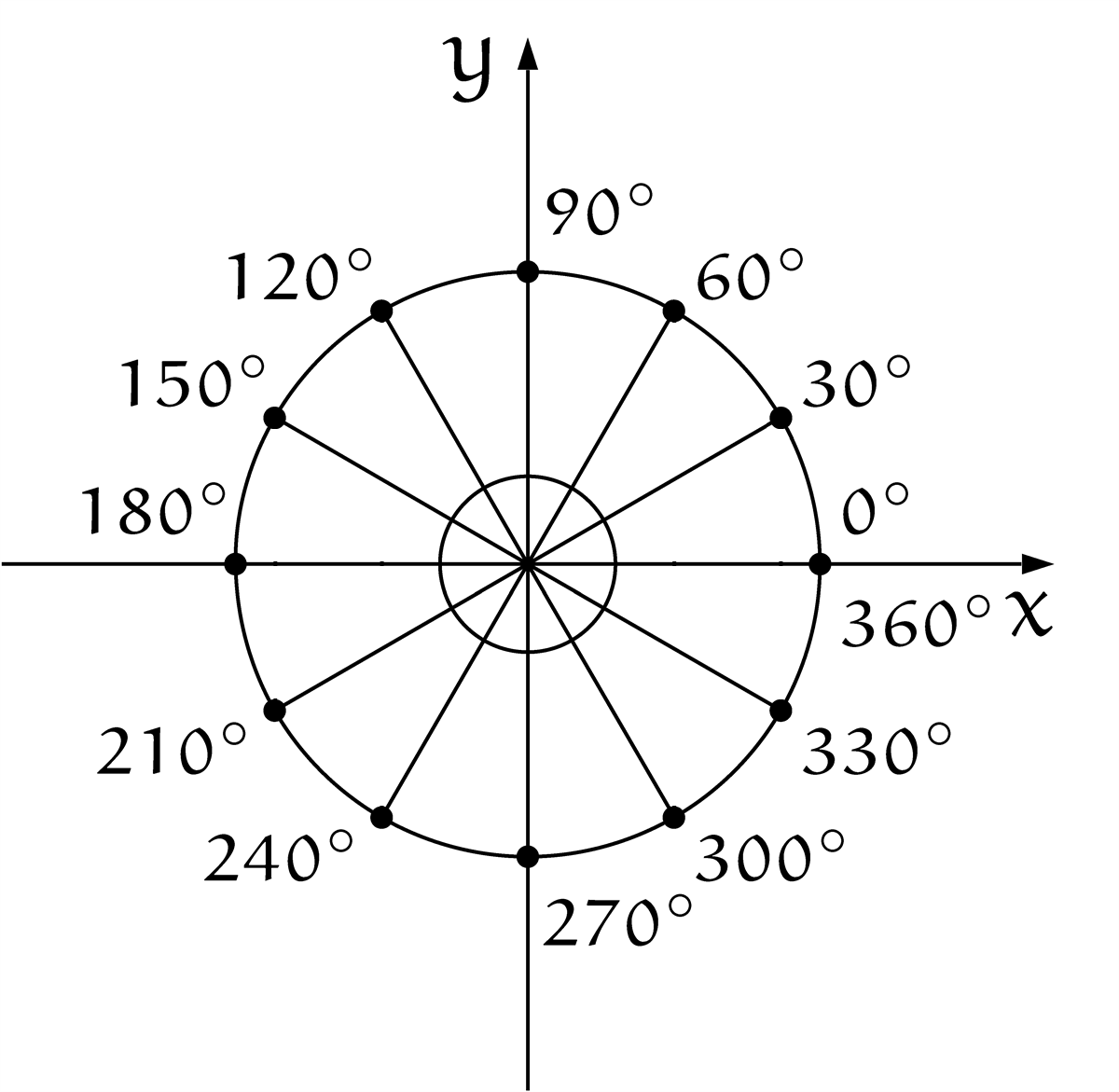
ユーリ「ほーほー。 $360^\circ$ でぐるっと回るんだね」
僕「そうだね。 $360^\circ$ で $0^\circ$ に戻る」
ユーリ「そんでそんで?」
僕「単位円を使うと三角関数の定義ができるんだよ」
ユーリ「さんかくかんすー? 難しそー」
僕「そんなことないよ。単位円の円周上でぐるぐる回る点の《$x$ 座標がコサイン》で《$y$ 座標がサイン》なんだよ。それだけのこと」
ユーリ「あ、コサインとか、サインとか、聞いたことある」
僕「回転させたときの角度を $\theta$(シータ)とすると……」
ユーリ「『シータ。いい名前だね』」
僕「?」
ユーリ「ラピュタ、知らないの?」
僕「アニメは関係ない……いや、あるのかな。まあいいけど、とにかく角度を $\theta$ と書くことにすると、 $x$ 座標のことを $\cos \theta$(コサイン・シータ)と呼んで、 $y$ 座標のことを $\sin \theta$(サイン・シータ)と呼ぶんだよ」
単位円の円周上の点
$(x, y) = (\cos \theta, \sin \theta)$
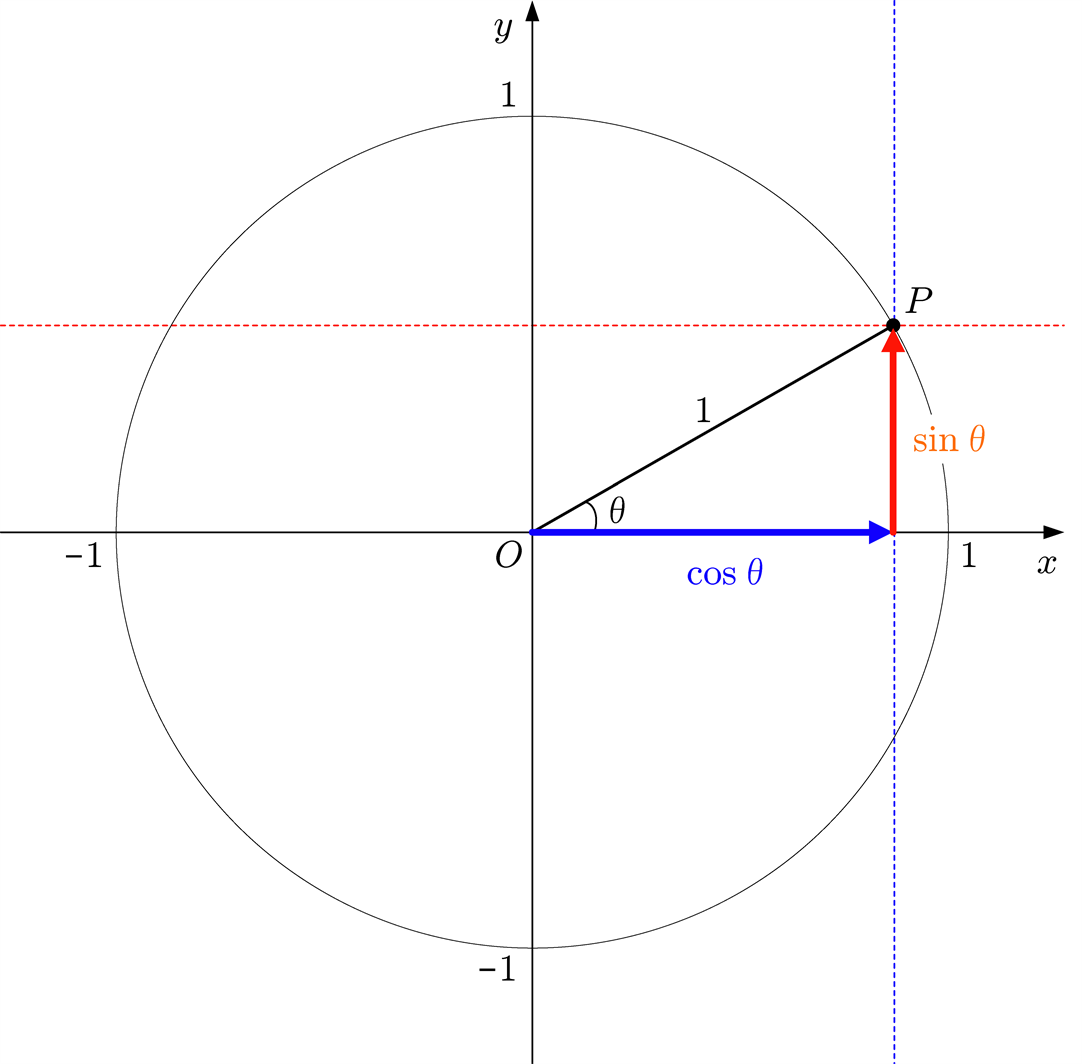
ユーリ「なんで?」
僕「いや、理由はないよ。これが $\cos \theta$ と $\sin \theta$ の定義なんだから。 単位円の円周上の点の座標を使って $\cos \theta$ と $\sin \theta$ を定義したんだ。 よく使うものだから名前を付けたと思ってもいいよ」
ユーリ「《コサインちゃん》と《サインくん》みたいに?」
僕「まあ、そうだね。三角関数っていうと難しそうだけれど、 単位円を描くと定義はすぐに覚えられるよね。コサインとサイン。 角度 $\theta$ を変えて点を回すと $x$ 座標と $y$ 座標もそれぞれ変わる。 それだけのことなんだ。 それだけのことなんだけど、三角関数を使うとおもしろい式がいろいろ……」
ユーリ「でたな数式マニア。でも、数式はもういいや。こっちの図は?」
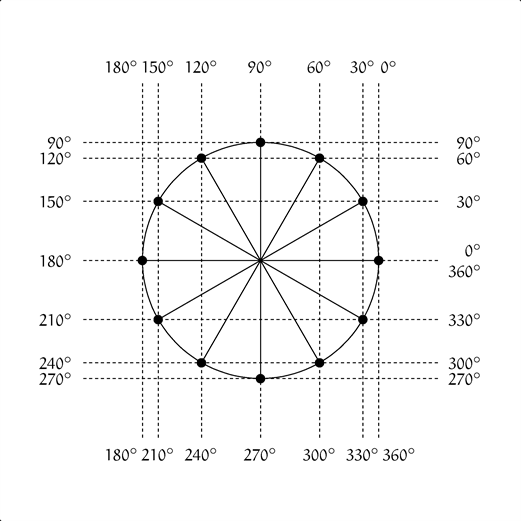
僕「ああ、これはお兄ちゃんが落書きしてたんだよ。何となく点を結んでね」
ユーリ「まわりの数字はなに?」
僕「え? 角度だよ。単位円の円周上の点が回転するとき、 $0^\circ$ だったらどの線になるか、 $30^\circ$ だったらどの線になるかを書き込んだんだ」
ユーリ「ふーん……」
点 $(x, y) = (\cos \theta, \sin \theta)$ が描く単位円
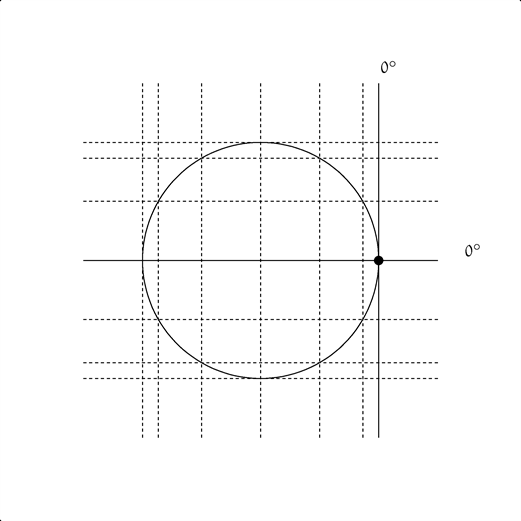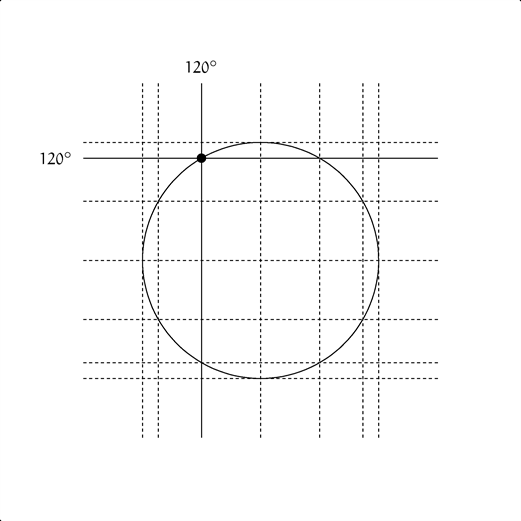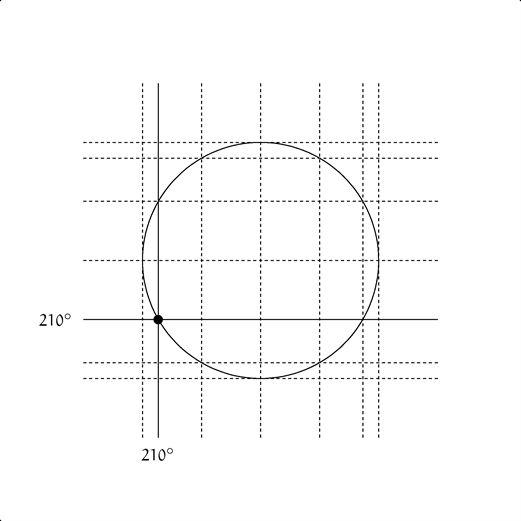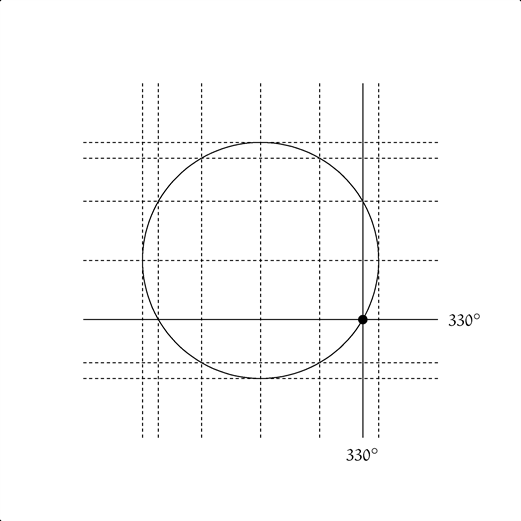
※プチ数学アニメは、アニメGIF表示可能環境のみで閲覧可能です。
ユーリ「……ところで、お兄ちゃん。これって時計みたい」

僕「そうだね。角度は時計の進む向きとは逆回りだけどね。 たまたま $30^\circ$ ずつに区切ったから、ちょうど $12$ に分かれて、 しかも、中心から回りに広がっている線もあるし」
ユーリ「線を書かなくても時計っぽいよー」

僕「まあ、そうかな」
ユーリ「お兄ちゃん、タテヨコの交差点を円がビシッと通るの、キモチいいよね」
僕「そうだね……ねえユーリ、 数学では交差点じゃなくて交点っていうんだよ。確かに道路の交差点と似てるけど」
ユーリ「タテ線とヨコ線のあいだが広くなったり狭くなったりして、こーてんが丸く並ぶの、おもしろいにゃ」
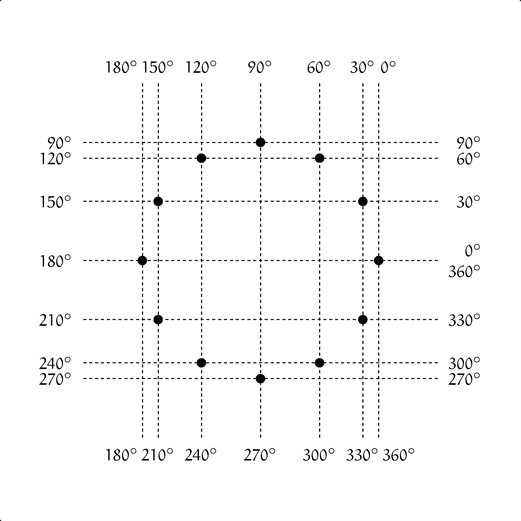
ユーリは図をながめている。 何かを考えているようだ。 しばらくたってから、ユーリは話し出す。
ユーリ「……ねーお兄ちゃん、タテの線とヨコの線って $7$ 本ずつあるじゃん?」
僕「そうだね。タテに $7$ 本、ヨコに $7$ 本」
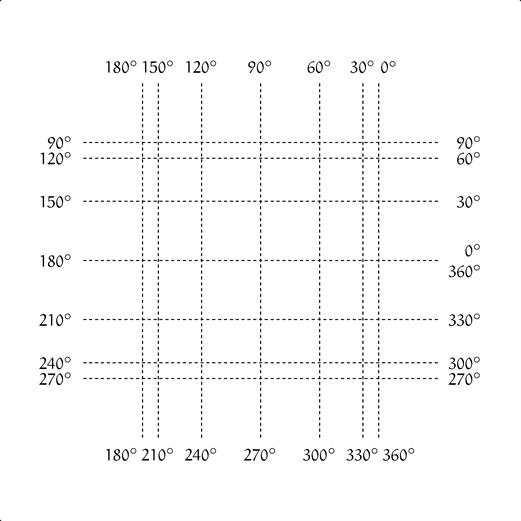
ユーリ「んで、 $7 \times 7 = 49$ で、 $49$ 個の交点があるわけじゃん?」
僕「そうだね」

ユーリ「$49$ 個も交点があるんだからさ、他の図形も描けそーじゃん!」
僕「ユーリ! それはおもしろい!」
ユーリ「わ、びっくりした! そんなにおもしろい?」
僕「うん、おもしろいことを思い出した。これから他の図形を作ってみよう」
ユーリ「?」
僕「さっき、単位円で、 $x$ 座標が $\cos \theta$ で、 $y$ 座標が $\sin \theta$ という話をしたよね」
ユーリ「うん」
僕「そこでは、両方とも同じ角度 $\theta$ を使っていた」
ユーリ「うん?」
僕「逆にいえば、 $\cos$ と $\sin$ に同じ角度 $\theta$ を与えると、単位円ができたわけだね」
ユーリ「うん……それで?」
僕「ではね、 $\cos$ と $\sin$ に渡す角度を $30^\circ$ ずらしてみよう。たとえば $\sin$ の方を $30^\circ$ 先に進める。そうしたら、どんな図形ができるだろうか」
ユーリ「なに言ってるかわかんない。難しーよ」
僕「簡単な話だよ。図で説明しようか。たとえば、タテとヨコの両方が $0^\circ$ の線のときはこの点になる」
$(x, y) = (\cos 0^\circ, \sin 0^\circ)$
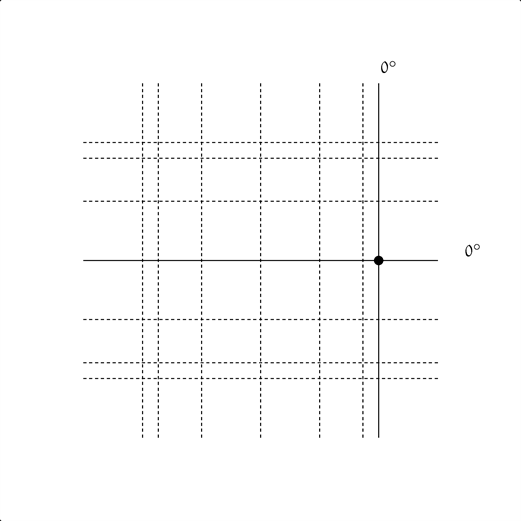
ユーリ「うん」
僕「この点 $(\cos 0^\circ, \sin 0^\circ)$ からスタートしてぐるっと回れば、単位円ができたわけだ」

ユーリ「うん、それで?」
僕「これから、 $\sin$ を $30^\circ$ 先に進めたらどんな図形ができるかを考えよう。 《$\sin$ を $30^\circ$ 先に進める》というのは《ヨコ線を一歩先に進める》ってことだよ。 つまりこの点 $(\cos 0^\circ, \sin 30^\circ)$ からスタートするんだ」
$(x, y) = (\cos 0^\circ, \sin 30^\circ)$
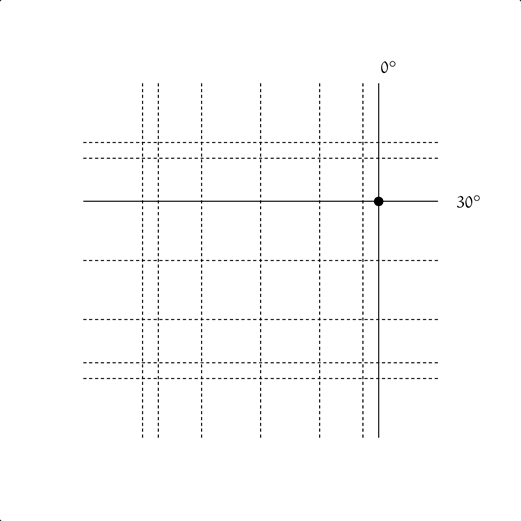
ユーリ「ほほー。なるほど。ヨコ線を上げたんだね。そーすると、どーなるの?」
僕「それが問題だよ。ヨコ線を、タテ線よりいつも $30^\circ$ 進めた状態で、ぐるっと回したらどうなるかな?」
ユーリ「む、むー……」
問題
$(x, y) = (\cos \theta, \sin \theta)$ では単位円ができる。

$(x, y) = (\cos \theta, \sin (\theta + 30^\circ))$ ではどんな図形ができる?
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2013年4月5日)
この記事は『数学ガールの秘密ノート/丸い三角関数』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!