第19回 シーズン2 エピソード9

ぐるぐるワンの作り方（前編）

僕の部屋

ユーリ「ねーお兄ちゃん！　目、つぶって！」

僕「三つ、ぶって？」

ユーリ「いきなりバイオレンスですか！　メ・ヲ・ツ・ブ・ッ・テ！」

僕「日本語でお願いしまーす」

ユーリ「……いいから目をつぶるんじゃー！」

僕「はいはい」

ユーリは中学二年生、僕の従妹（いとこ）だ。 まあ、従妹っていっても、小さい頃からいっしょに遊んでたから兄妹みたいなものだけれど。 ユーリはしょっちゅう僕の部屋に遊びに来てはおしゃべりしていく。

時計パズル

ユーリ「じゃじゃーん！　目、開けていいよ」

僕が目を開けると、こんなものが机に置かれていた。

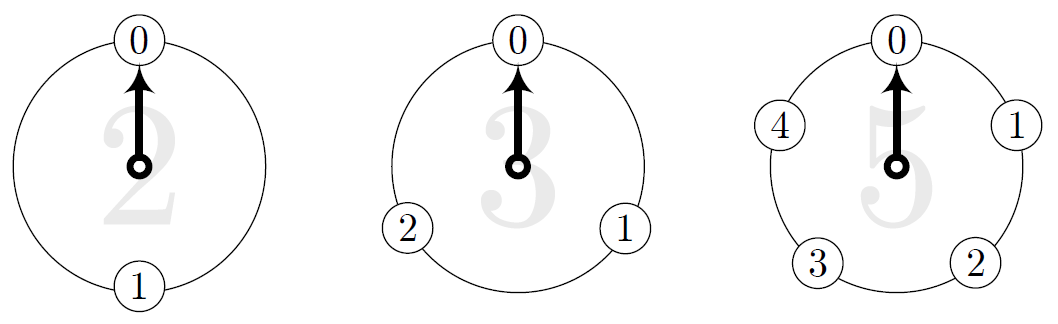
僕「何この変な機械」

ユーリ「変な機械ってゆーなー！」

僕「だって変だからね」

ユーリ「これ、時計パズルなんだよ」

僕「時計パズル？」

ユーリ「そだよん。ほら時計が三つ並んでるっしょ？」

僕は、三つ並んだ時計を順番に観察する。

三つの時計

僕「時計といっても、針は一つだし、この左端の時計には数字が二つしかないな」

ユーリ「そこがパズルだよねー。これ《$2$ の時計》ってゆーんだよ」

《$2$ の時計》

僕「真ん中にある時計は文字盤に数字が三つあると」

ユーリ「そだね。これは《$3$ の時計》だよ」

《$3$ の時計》

僕「そして右端の時計は数字が五つと。これは《$5$ の時計》かな」

ユーリ「そーそー。ねねね、おもしろそーっしょ？」

《$5$ の時計》

時計パズルを動かす

僕「確かにおもしろそうだけれど、これでどうやって時間を計るの？　止まってるみたいだけど」

ユーリ「あのね、これって自動で時間を計るんじゃないんだよ。数を数えるの」

僕「ほほう？」

ユーリ「ほらここにボタンが二つあるじゃん？」

僕「あるね。リセット（RESET）とカウント（COUNT）と書いてある」

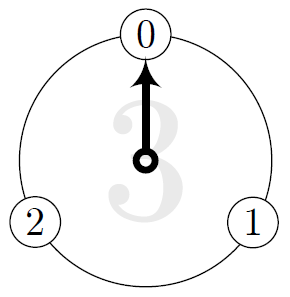
ユーリ「リセットボタンを《カチャッ》て押すと、三つの時計の針はこんなふうに全部 $0$ に戻るの。 時計パズルはここからスタートすんだよ。えっと、パターン $0,0,0$ だにゃ」

リセットボタンを押すと、全部 $0$ に戻る（パターン $0,0,0$）

僕「うん、いいよ。それで？」

ユーリはけんめいに時計パズルとやらの説明をしてくれる。 いつもはすぐに《めんどい！》って叫ぶくせに、 こういうときは意外に粘り強いんだな。

ユーリ「そんでね、カウントってボタンを $1$ 回《カチャッ》って押すと、ほらほら、針が進んだっしょ？」

僕「なるほど。カウントボタンを押すと、三つの時計の針が同時に $1$ だけ進むんだね」

カウントボタンを押すと、三つの時計の針が $1$ 進む（パターン $1,1,1$）

ユーリ「ほらほら、お兄ちゃん。よく見なきゃだめだよ」

今日のユーリはちょっと先生っぽいしゃべりかただな。 先生っぽいというか……いつもの僕の話し方みたいだ。

僕「はいはい。見てますよ。ユーリ先生」

ユーリ「針はどんなふーに進んだかわかる？」

僕「三つの時計の針が全部 $1$ ずつ進んで、 $1$ が並んだね。パターン $1,1,1$ になった」

ユーリ「カウントボタンをもっかい押したらどーなると思う？」

僕「そりゃ、全部 $1$ ずつ進むだろうね」

ユーリ「やってみよー！　《カチャッ》」

パターン $0,2,2$

僕「そらね。全部 $1$ ずつ進んだ。お兄ちゃんの言った通りだよ。パターン $0,2,2$ になった」

ユーリ「確かにそーなんだけど、《$2$ の時計》の針は $0$ に戻ったっしょ？　だから、 《針は進んでも数が大きくなるとは限らない》のが重要ポイント。はい、ここ試験に出ます」

僕「なに言ってるんだよ」

ユーリ「へへー」

僕「でも、確かにそこは大事だな。ねえ、ユーリ。お兄ちゃんにもカウントボタン押させてほしいな」

ユーリ「いいよん」

僕はカウントボタンを《カチャッ》と押す。針がまた $1$ ずつ進んだ。 《$2$ の時計》の針は $1$ になり、《$3$ の時計》の針は $0$ に、そして《$5$ の時計》の針は $3$ になった。 パターン $1,0,3$ だ。

パターン $1,0,3$

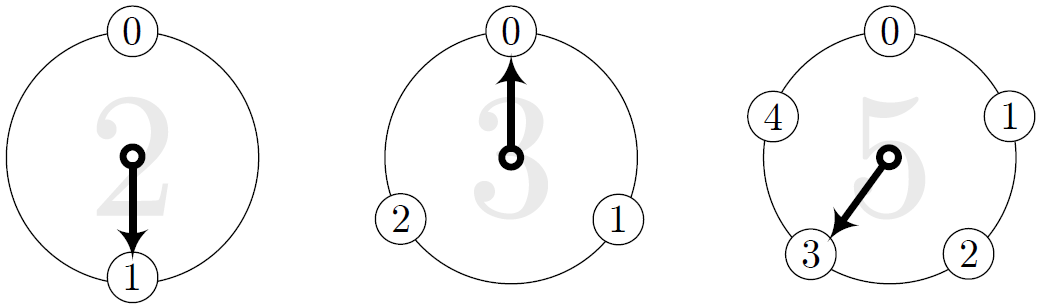
僕「これはなかなか…楽しいな。《$3$ の時計》が $0$ になった」

ユーリ「だよねー。ぐるっと戻った」

さらに僕はカウントボタンを《カチャッ》と押す。針がまた $1$ ずつ進んだ。 《$2$ の時計》の針は $0$ になり、《$3$ の時計》の針は $1$ に、そして《$5$ の時計》の針は $4$ になった。 パターン $0,1,4$ だ。

パターン $0,1,4$

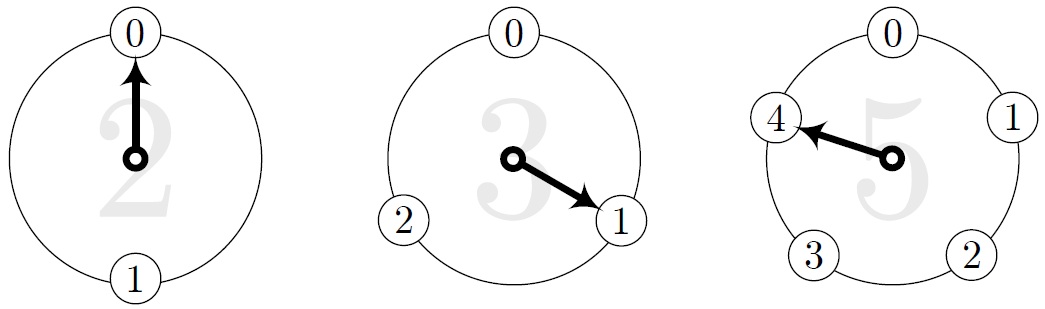
僕「ここでさらにもう一回押すと、《$5$ の時計》が $0$ になるな。《カチャッ》」

ユーリ「ぐるっと戻ったねー」

パターン $1,2,0$

僕はボタンを《カチャッ》と押す。針がまた $1$ ずつ進んだ。

僕「ふむ。今度は左の時計二つが $0$ を指すと……」

パターン $0,0,1$

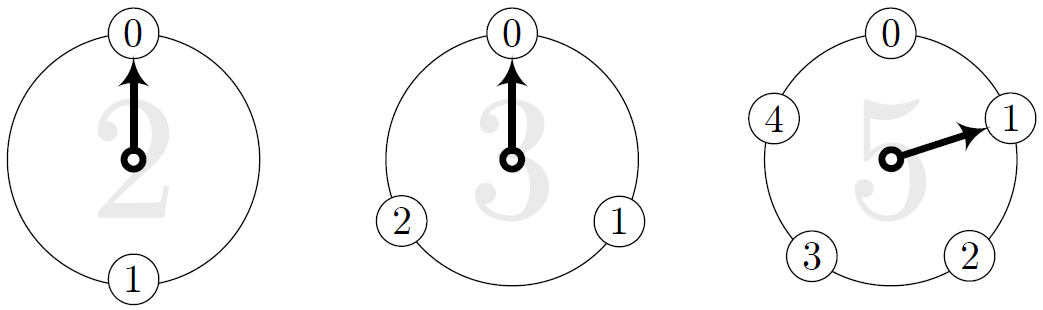
ユーリ「はい！　お兄ちゃん、そこでストップしてねー」

僕「どうして？」

ユーリ「お兄ちゃん、ここまで何回押したか覚えてる？」

僕「え？　 $5$ 回、いや、 $6$ 回か。うん、 $6$ 回だ」

時計パズルの問題

ユーリ「はい、それではここで時計パズルの問題でーす」

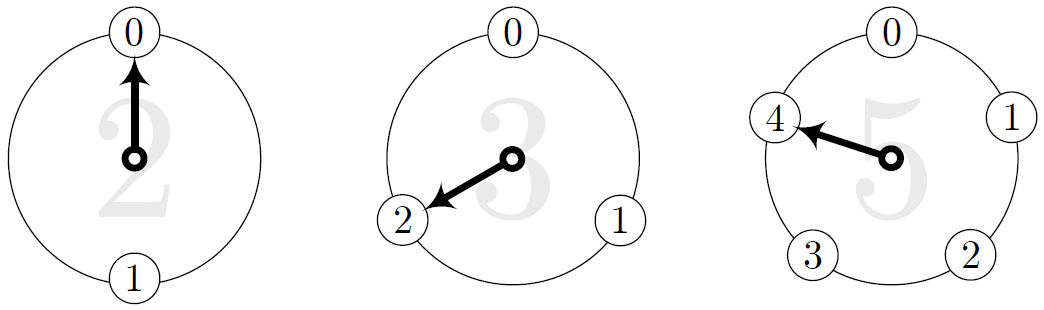
僕「なるほど。ぱっと見にはわからないな」

ユーリ「ほれほれ、カウントボタン押さないでもわかるかにゃ？」