第18回 シーズン2 エピソード8

選べないのに見える数（後編）

図書室にて

テトラ「あ、あの……先輩がおっしゃっていた《ゼロと単数と合成数を除いて素数を求める》という意味が、 とてもよくわかりました。《エラトステネスのふるい》は合成数を《ふるい》にかけて素数を求めているのですね……あれれ？」

僕「うん？」

テトラ「ひとつ疑問がわいてきました」

僕「というと？」

テトラ「《エラトステネスのふるい》はいいんですけれど、 合成数を選り分けて素数を求めるのではなく、 もっと直接に素数を求める方法はないんでしょうか？」

僕「直接に？」

テトラ「《エラトステネスのふるい》って、 $2$ の倍数を消していって、 $3$ の倍数を消していって、 $5$ の倍数を消していって……と進む方法ですよね」

僕「そうだね」

テトラ「そうやって数を消した《残り》が素数です」

僕「うん、テトラちゃんの言う通りだよ」

テトラ「合成数を消すことで素数が浮かび上がってくる感じですよね。 そうじゃなくて、素数を直接《はいこれ、はいこれ、はいこれ》ってピックアップはできないんでしょうか」

僕「テトラちゃんはおもしろいことをいうなあ。なるほど……いや、僕は知らないんだけど」

ミルカ「何をしてる？」

テトラ「あ、ミルカさん！　ちょうどいいところに」

ミルカさんは、長い黒髪の饒舌才媛。 数学がとても得意で、僕たちを数学の世界に導くリーダー的存在だ。 彼女はメタルフレームの眼鏡をくいっと上げ、僕たちのノートを見る。

ミルカ「ふうん。《エラトステネスのふるい》か」

テトラ「はい！　……やっぱりみなさんご存じなんですね」

ミルカ「どうして、こう並べた？」

ミルカさんはノートの表を指さす。

$0$ 以上の整数の表

テトラ「ええっと、あの……あれれ、でも、《エラトステネスのふるい》は $0$ 以上の整数から、 $0$ を消して、 $1$ を消して、 $2$ は素数で、 $2$ の倍数を消して、 $3$ は素数で、 $3$ の倍数を消して……」

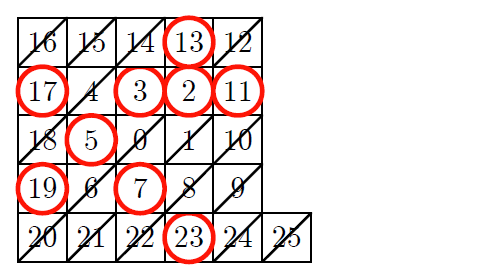
ミルカ「それはいい。《ふるい》を掛けた後はこうなって、赤丸の部分が素数なのだろう？」

《エラトステネスのふるい》を掛けた後の表（赤丸が素数）

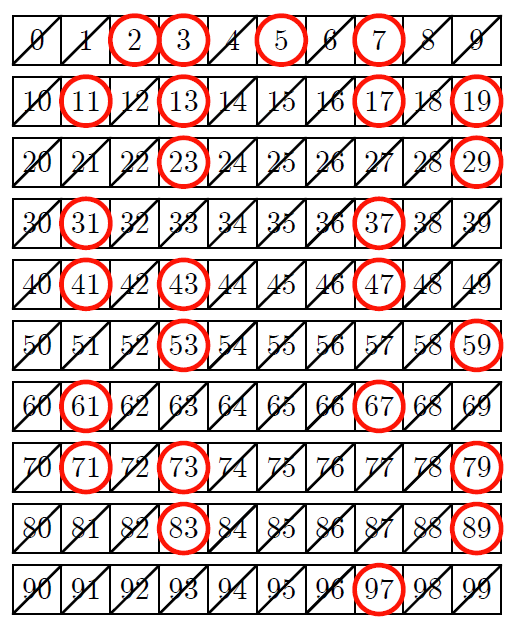
テトラ「は、はい……そうですが。ええと、この表は先輩が」

僕「うん、僕が書いたんだよ。何かおかしいかな、ミルカさん」

ミルカ「おかしくはない。理由を聞いているだけ。君は、どうしてこう並べた？」

僕「どうしてって、特に理由はないよ。 区切りよく $10$ 個ずつ $1$ 行にまとめると消しやすいってくらいで」

ミルカ「テトラ。 $0$ 以上の整数はどう並べたくなる？」

テトラ「え、あ、そうですね……あたしなら、数列なので一列にこう」

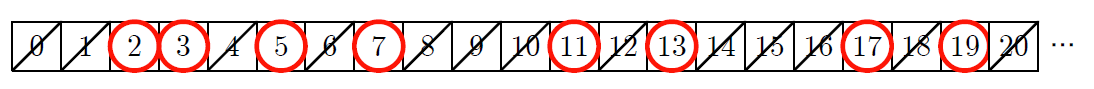
ミルカ「それもいい」

テトラ「でも、これだとノートの幅がすごおおおく長くないと不便ですね」

テトラちゃんは両手を思いっきり広げる。

僕「でも、いずれにせよ $0$ 以上の整数は無数にあるんだから、いくら長くても足りなくなるよ。 どこかで折り返さなきゃね」

ミルカ「だとしても $10$ 個ずつ折り返さなければいけないという法はないな」

テトラ「あ！　こうしたらどうでしょう。たとえば $2$ 個ずつ折り返すんです」

ミルカ「ふむ？」

テトラ「ああっ！　発見ですっ！　これだとタテに見たとき、左の列には赤丸が $2$ しかありませんっ！　 $2$ 以外の素数はすべて右の列に！」

僕「それは……あたりまえじゃないかな。だって、素数のうち偶数なのは $2$ だけだから。 $2$ 以外の素数はすべて奇数で、すべての奇数は右の列にあるんだからね」

テトラ「あ……そ、そうですよね。 うまく折り返したら《素数が見える》と思ったんですが……」

ミルカ「見ようか」

テトラ「はい？」

ミルカ「素数を、見ようか」

テトラ「……うまく折り返せば《素数が見える》んですか？」

ミルカ「まあね」

僕「え？」

素数を見よう

ミルカさんがノートに向かい、 僕とテトラちゃんは両側から彼女が書くのをのぞきこむ。

僕「それで？」

ミルカ「まずはゼロ（$0$）と単数（$1$）を並べる」

テトラ「さっきあたしが $2$ 個で折り返したのと同じですね」

ミルカ「テトラは下の行に進んだ。私は上に進もう」

テトラ「上……ですか？」

僕「でもこれだとさっきとは違うよね。 上に進むなら、 $0$ の上に $2$ を置くべきじゃない？」

ミルカ「そうしたら、テトラと同じ表になるだろう？」

僕「まあ、そうだけど」

テトラ「次はどうするんですか？」

ミルカ「左へ進む。 $3$ だ」

テトラ「なるほど。次は、上に進んで $4$ ですね！」

ミルカ「いや、違う」

テトラ「あれれ？」

ミルカ「$4$ は、左に進む」

テトラ「はみ出しちゃいました」

僕「だとするなら、次は上に進んで $5$ かなあ」

ミルカ「いや、次の $5$ は下に進む」

僕「？」

テトラ「次の $6$ は左でしょうか……」

ミルカ「いや。 $6$ はさらに下」

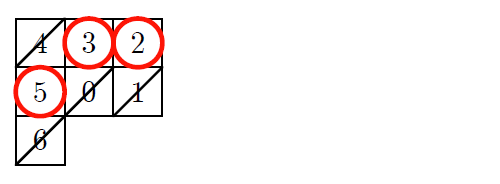
テトラ「始めは右で、次が上、左、左、下、下…？　→↑←←↓↓？」

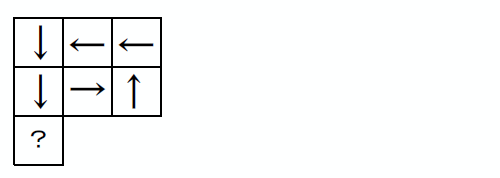
僕「あ、わかった！　ぐるっと回っているんだね、ミルカさん！」

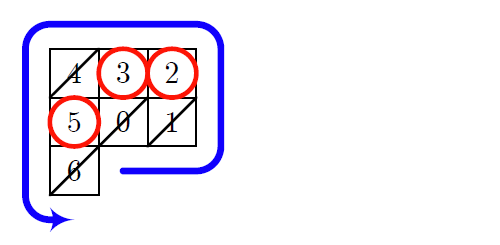
ミルカ「ビンゴ」

ミルカさんはウインクして指を鳴らした。

テトラ「ははあ……」

僕「ということは、 $7, 8, 9$ はずっと右に進むんだね」

ミルカ「その通り」

テトラ「すると、次の $10, 11, 12$ は上に進むんですか」

ミルカ「そうだ」

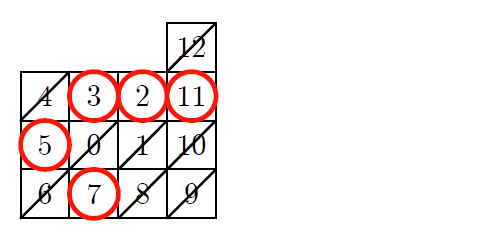
僕「ねえミルカさん。ぐるっと回りながら数を書いていくと《何かおもしろいこと》が起きるの？」

ミルカさんは顔を上げて僕を正面から見すえた。

ミルカ「君は、自分で見つけたいの？　私に教えてほしいの？」

僕「わかった、わかった。そうだよね。続けていこう」

テトラ「次は、ええと……はい、 $16$ までは左に進みます」

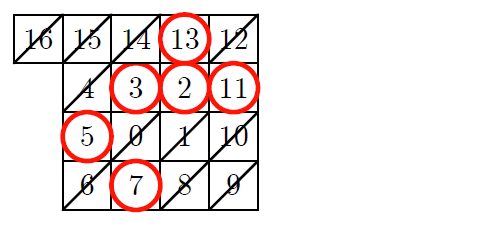
僕「$20$ までは下に進むんだね」

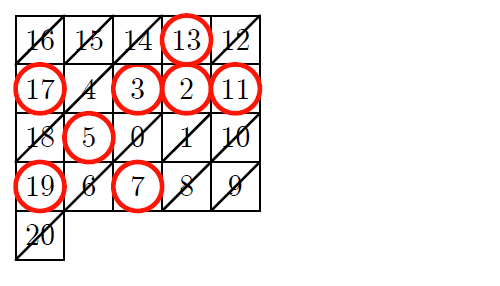
テトラ「次は $25$ まで右です。はいはいはい！」

テトラちゃんが大きく右手を挙げてぶんぶん振っている。

僕「どうしたの？」

ミルカ「気づいた？」