![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/整数で遊ぼう』として書籍化されています。
ここは高校の図書室。 放課後になったので、僕はいつものようにここにやってきた。 後輩の元気少女テトラちゃんが本をじっと見つめていた。
僕「テトラちゃん、難しい顔してるね」
テトラ「あ、先輩! そ、そうですか……そんなに難しい顔してました? すみません」
僕「いやいや、別に謝らなくてもいいよ。数学の問題?」
テトラ「いえ、この参考書に書いてあるエラトステネスのふるいの説明を読んでたんです」
僕「ああ、素数を求める方法だね」
テトラ「あ、やはりご存じでしたか」
僕「うん、素数が出てくるところでは必ず《エラトステネスのふるい》の話題が出てくるからね。 特に数学の読み物ではね」
テトラ「そうなんですか……」
僕「でも、そんなに難しくなかったように思うけどなあ」
僕はそういってテトラちゃんの隣に座る。 テトラちゃんはいつも甘い香りがする。
テトラ「そうなんですか? この本にはあまり詳しく書いてないんです。 エラトステネスさんが人の名前で、 とても賢い人だということはわかったんですが、 あとは 《順番に倍数を消していくと素数が現れてくる》という説明と、 数の表が書かれているだけで……」
僕「どれどれ……ああ、そうだね。これじゃよくわからないかな。 ぜんぜん難しい話じゃないよ。数の表を作って、倍数を実際に消してみればいい。 やってみようか」
テトラ「はい、お願いします」
僕「《エラトステネスのふるい》はね……」
テトラ「あ、すみません。お話の前に確めたいんですが、素数の定義はこれでいいですよね?」
素数の定義
$2$ 以上の整数で、 $1$ と自分自身以外に約数を持たない数を素数という。
僕「うん、それでいいよ。具体的に素数をいくつか言える? 小さい方から」
テトラ「はい、まず $2$ ですよね。それから $3$ です。あとは $5$ と、 $7$ と、次は $11$ ですか」
僕「そうだね。テトラちゃんがいま飛ばした $4$ や $6$ や $8, 9, 10$ は合成数というよ」
テトラ「合成数ですか……どうしてそういう名前なんですか?」
僕「合成数というのは《$2$ 個以上の素数を掛け算して作る数》だからね。 素数を素材にして合成した数という意味なんだと思うよ」
テトラ「ははあ」
僕「$2$ 以上の整数を、素数の積で表わしてみると、素数と合成数は一目で区別できるよ。合成数は積の形になるから」
$$ \begin{array}{rcll} 2 &=& 2 & \REMTEXT{素数} \\ 3 &=& 3 & \REMTEXT{素数} \\ 4 &=& 2 \times 2 & \REMTEXT{合成数(素数$2$と素数$2$の積)} \\ 5 &=& 5 & \REMTEXT{素数} \\ 6 &=& 2 \times 3 & \REMTEXT{合成数(素数$2$と素数$3$の積)} \\ 7 &=& 7 & \REMTEXT{素数} \\ 8 &=& 2 \times 2 \times 2 & \REMTEXT{合成数(素数$2$と素数$2$と素数$2$の積)} \\ 9 &=& 3 \times 3 & \REMTEXT{合成数(素数$3$と素数$3$の積)} \\ 10 &=& 2 \times 5 & \REMTEXT{合成数(素数$2$と素数$5$の積)} \\ \end{array} $$テトラ「ははあ……合成数は $4 = 2 \times 2$ や $6 = 2 \times 3$ のように掛け算が出てくるのですね」
僕「そうそう。 合成数は《$2$ 個以上の素数の掛け算》の形になるけれど、 素数は《$2$ 個以上の素数の掛け算》の形にはならない」
テトラ「あれ? $1$ はどうなるんですか」
僕「$1$ は合成数でも素数でもないよ」
テトラ「そうなんですか」
僕「$1$ 自身は素数じゃないし、 $1$ は素数の積で表すこともできないからね。 $1$ は単数というよ」
テトラ「単数に素数に合成数に……」
僕「あとはゼロだね。ゼロ($0$)は単数でも素数でも合成数でもないなあ」
テトラ「何だかごちゃごちゃしてきましたあ!」
僕「整理すれば大丈夫、難しい話じゃないんだから。 $0$ 以上の整数($0, 1, 2, 3, \ldots$)はきれいに分類できる。 もれもないし、だぶりもない」
$0$ 以上の整数($0, 1, 2, 3, \ldots$)の分類
$$ \begin{array}{llllllllllllllllll} \REMTEXT{ゼロ} &\REMTEXT{:}& 0 & \\ \REMTEXT{単数} &\REMTEXT{:}& & 1 & \\ \REMTEXT{素数} &\REMTEXT{:}& & & 2,& 3,& & 5,& & 7,& & & & 11,& & \ldots \\ \REMTEXT{合成数} &\REMTEXT{:}& & & & & 4,& & 6,& & 8,& 9,& 10,& & 12,& \ldots \\ \end{array} $$
テトラ「もれもないし、だぶりもない……」
僕「だからね、テトラちゃん」
テトラ「はい?」
僕「$0, 1, 2, 3, \ldots$ から、ゼロと単数と合成数を全部消したら——何が残る?」
テトラ「ええと……あ、素数ですか!」
僕「そうそう。素数が残る。 実はね、それが《エラトステネスのふるい》なんだよ。 ゼロ($0$)と単数($1$)はすぐに消せる。 あとは合成数を消してしまえばいい。 合成数を消して素数を求めるのが《エラトステネスのふるい》の仕組みなんだ」
テトラ「合成数を消して素数を求める! ……って、具体的にどうするんでしょう」
僕「たとえば $2$ という素数があったら、 $4, 6, 8, 10, \ldots$ のように、 《$2$ より大きな $2$ の倍数》を消すということだね」
テトラ「ははあ……」
僕「じゃあ、具体的に《エラトステネスのふるい》をやってみよう」
テトラ「はい!」
僕「まずは、 $0, 1, 2, 3, \ldots$ という表を作る。切りがないから $99$ までにしておくね」
テトラ「はい」
$0$ 以上 $99$ 以下の整数($0, 1, 2, 3, \ldots, 99$)の表
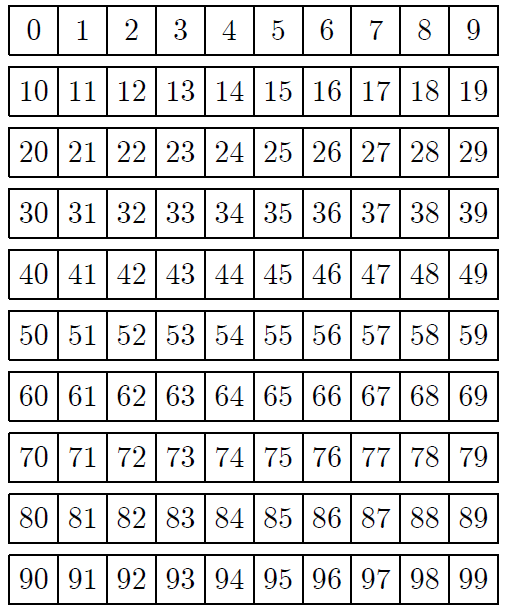
僕「まずはゼロ($0$)と単数($1$)を消す」
テトラ「これでいいですか」

僕「うん、いいよ。そして次の数 $2$ は、 $1$ と自分自身($2$)以外に約数を持たないから素数になる。マルをつけて」
テトラ「$2$ にマルを……はい、つけました。素数の印ですね」

僕「ここから $2$ を約数に持つ合成数を消していくよ。 要するに《$2$ より大きな $2$ の倍数を消していく》んだ」
テトラ「ということは、 $4$ と、 $6$ と、 $8$ と、 $10$ と、 $12$ と、 $14$ と、 $16$ と、 $18$ と……って、一つおきですから 消すのは楽ですね」
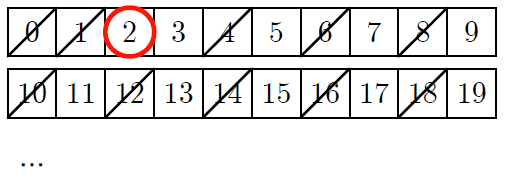
僕「そうだね。《$2$ の倍数を消す》ということは《$2$ で割り切れる数を消す》ということだよね」
テトラ「$20, 22, 24, 26, \ldots$」
僕「ねえ、テトラちゃん」
テトラ「$28, 30, 32, \ldots$」
僕「テトラちゃん?」
テトラ「……は、はいっ?」
僕「《$2$ の倍数を消す》ということは《$2$ で割り切れる数を消す》ということだよね」
テトラ「ええと……あ、はい、そうですね」
僕「さらに言い換えれば《$2$ の倍数を消す》ということは《$2$ を約数に持つ数を消す》ということになるね。 《$2$ の倍数》っていうのは《$2$ を約数に持つ数》のことだから」
テトラ「はい、わかります」
僕「だから、《$2$ より大きな $2$ の倍数を消す》というのは、 《$2$ を約数に持つ合成数を消す》ことになる」
テトラ「確かに! ……ちょっ、ちょっとすみません。消している途中だったので、 $2$ を約数に持つ合成数をぜんぶ消しちゃいます! $34, 36, \ldots$」
僕「……消したね」
テトラ「消えましたね。 $2$ より大きな $2$ の倍数は全部消えました」
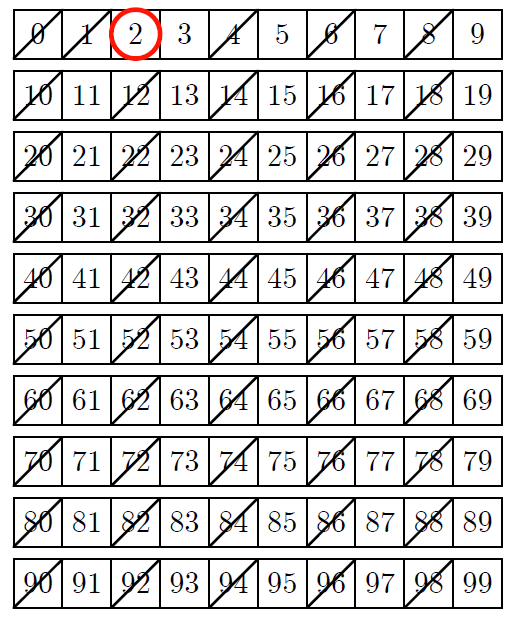
僕「表の中で《消えていない最小の数》を見ると $3$ になっている。だから、 $3$ が次の素数になる」
テトラ「どうしてそう言えるんですか?」
僕「どうしてかというと、 $3$ は、 $1$ と自分自身以外の約数を持たないことになるからだよ。 だって、 $3$ より小さな数のうち素数は $2$ だけ。しかも、 $3$ は $2$ の倍数じゃない。つまり、 $3$ は $2$ を約数に持たない」
テトラ「確かに $3$ は $2$ の倍数じゃありませんが……」
僕「だって、もし $3$ が $2$ の倍数だったら、いまごろ消えているはずだからね!」
テトラ「あ! それはそうですね。 $2$ の倍数をいま消したんですから! わかりました、消えてない一番小さな数の $3$ が次の素数ですね」
僕「その通り! $3$ にマルをつけよう」
テトラ「はい!」
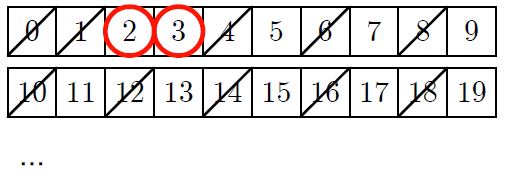
僕「今度は、 $3$ より大きな $3$ の倍数を消していくんだ。 $6, 9, 12, 15, 18, \ldots$ だね」
テトラ「ははあ……なるほど。さっきと同じですね。あれ? $6$ はもう消えてます」
僕「$6$ は $2$ の倍数でもあるからね」
テトラ「それはそうですね。おもしろいです。でも、いちおう改めて消します」
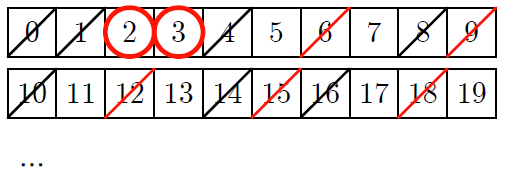
僕「$3$ の倍数を消そうとして、すでに消えていた数は $6$ の倍数になるんだよ。 $2$ の倍数でもあるし、 $3$ の倍数でもあるから」
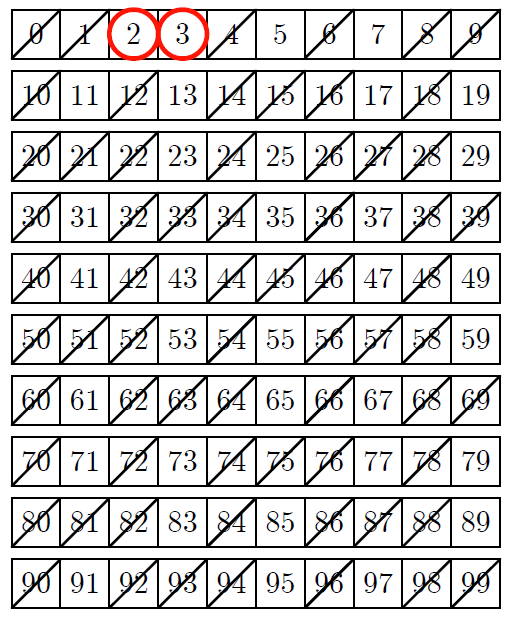
テトラ「そうですね! ……はい、できました。 $3$ の倍数も全部消しました」
僕「次に生き残っている数は何かな?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2013年2月22日)
この記事は『数学ガールの秘密ノート/整数で遊ぼう』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!