![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/整数で遊ぼう』として書籍化されています。
高校二年生の僕は、中学二年生のいとこのユーリと数学トークを続けている。 ユーリが持ってきた数当てマジックの背後にある数学をわかりやすく説明しようとしていると……
僕「ユーリの数当てマジックで《数を当てる方法》は簡単だよね」
ユーリ「そーだね」
数当てマジック
これから、あなたの好きな日を当ててみせましょう。
何月でもかまわないので、好きな日の数を思い浮かべてください。
・2月14日が好きなら→14
・3月16日が好きなら→16
・12月24日が好きなら→24
思い浮かべたら、5枚のカードのうち、 《その数が出てくるカード》だけをすべて表にしてください。
《その数が出てこないカード》は裏返しに伏せてください。

僕「数を当てるには、表になったカードの左上の数を足すんだろ?」
ユーリ「そーそー、それだけで思い浮かべた数を当てられるんだよー」
数を当てる方法
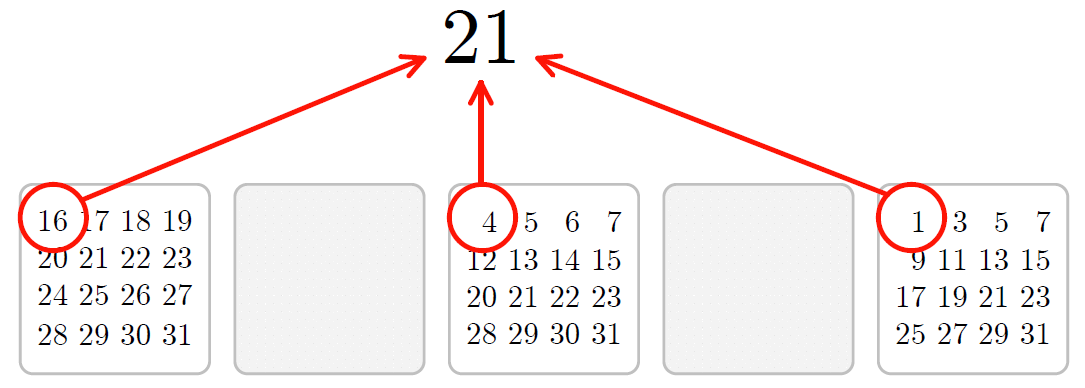
相手が選んだカードの左上の数を足せば、相手が選んだ数になる。
相手が $21$ を選んだときのようす
相手が $12$ を選んだときのようす

僕「そうだね。《数を当てる方法》はそれでいい。 理屈はわからなくてもマジックはできる。 でも、《数が当たる理由》がわからないとつまらない」
ユーリ「まーね」
僕「こんなふうに対応表を作れば、《$5$ 枚のカードの置き方》と《$0$ 〜 $31$ の整数》とを対応づけられる」
《$5$ 枚のカードの置き方》と《$0$ 〜 $31$ の整数》の対応表(×は裏、○は表)

ユーリ「うん」
僕「対応表が作れるんだから、 $0$ 〜 $31$ の範囲のどんな整数でも《$5$ 枚のカードの表裏の置き方》で表せる」
ユーリ「そーだね。この対応表に書いてあるもん」
僕「実は、理屈がわかってしまえば、対応表を見なくても、 $0$ 〜 $31$ の範囲の整数がどんな表裏の置き方になるかはわかるんだ」
ユーリ「カード見ればわかるよ」
僕「カードを見なくてもわかる。そのためにはカードの《左上の数》を研究すればいい。 《数を当てるときに足す数》がこれなんだから」
ユーリ「数を研究するってかっこいいにゃ!」
数当てマジックで《数を当てるときに足す数》
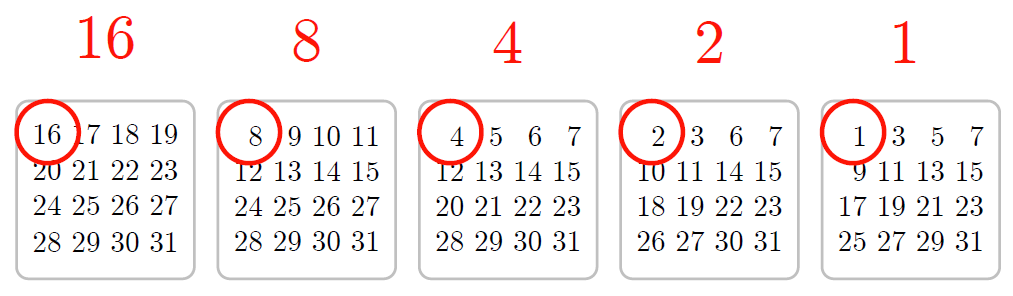
僕「さあ、この数が何なのか、わかるかな?」
$$ 16 \qquad 8 \qquad 4 \qquad 2 \qquad 1 $$ユーリ「わかるよ。偶数だ!……んにゃ、ちがう。 $1$ があるか」
僕「でも、いいセンいってる。これはね《$2$ の冪乗》というんだよ」
ユーリ「$2$ のべきじょう?」
僕「そう。 $2$ の冪乗は、 $2$ を何個か掛けてできる数だね。 $2$ の累乗ということもあるよ。 $2$ を $n$ 個掛けるなら、 $2^n$ と書く」
$2$ の冪乗
$$ \begin{array}{rclcl} 16 &=& \underbrace{2 \times 2 \times 2 \times 2}_{\REMTEXT{$4$個}} &=& 2^4 \\ 8 &=& \underbrace{2 \times 2 \times 2}_{\REMTEXT{$3$個}} &=& 2^3 \\ 4 &=& \underbrace{2 \times 2}_{\REMTEXT{$2$個}} &=& 2^2 \\ 2 &=& \underbrace{2}_{\REMTEXT{$1$個}} &=& 2^1 \\ \end{array} $$
ユーリ「あれ? でも $1$ は? $1$ は $2$ を掛けてできてるわけじゃないよ?」
僕「《$2$ の $0$ 乗》は $1$ に等しいと定義する」
ユーリ「てーぎ?」
僕「こう決めたってこと」
$$ 1 = 2^0 $$ユーリ「$0$ 乗……?」
僕「$2^0$ は $1$ と定義されてる。これは指数法則のため。 まあ、むりやり《$0$ 個掛ける》と見なすこともできるけどね。 こんなふうに頭に $1$ を掛けて考えれば」
$$ \begin{array}{rclll} 16 &=& 1 \times 2 \times 2 \times 2 \times 2 & = 2^4 & \REMTEXT{($2$を$4$個掛けた)} \\ 8 &=& 1 \times 2 \times 2 \times 2 & = 2^3 & \REMTEXT{($2$を$3$個掛けた)} \\ 4 &=& 1 \times 2 \times 2 & = 2^2 & \REMTEXT{($2$を$2$個掛けた)} \\ 2 &=& 1 \times 2 & = 2^1 & \REMTEXT{($2$を$1$個掛けた)} \\ 1 &=& 1 & = 2^0 & \REMTEXT{($2$を$0$個掛けた)} \\ \end{array} $$ユーリ「ほほー」
僕「さて、改めて……この数当てマジックの鍵になる数は《$2$ の冪乗》だ」
ユーリ「うん」
僕「数当てマジックをするためには、 《$16, 8, 4, 2, 1$ のどれかを足し合わせれば、 $0$ 〜 $31$ のどんな整数でも作れる》ことがポイントになる。 でないと《$5$ 枚のカードで、 $0$ 〜 $31$ の整数を表す》ことができない」
ユーリ「ふんふん」
僕「実は、与えられた $0$ 〜 $31$ から、どのカードを表にすればいいのかは、《計算》すればわかる」
ユーリ「けーさん?」
僕「たとえば $21$ をカードで表すとしよう。 そのために《割ってあまりを求める》という計算を繰り返すんだ」
ユーリ「割り算するってこと?」
僕「うん。繰り返して割り算する。 $21$ で具体的にやってみよう。 $21$ を $2^4$ つまり $16$ で割ると「商は $1$」で「あまりは $5$」だね」
ユーリ「商って何だっけ」
僕「割り算の答えだよ。 $21$ を $16$ で割ると、「$1$ あまり $5$」になる」
$$ 21 \div 16 = 1 \REMTEXT{あまり} 5 $$ユーリ「うん」
僕「次に《あまりの $5$》を今度は $2^3$ つまり $8$ で割る。 そんなふうに、《割ってあまりを求める》という計算を繰り返すんだ。そして商に注目する」
$$ \begin{array}{rcll} 21 \div 16 &=& \underline{1} \REMTEXT{あまり} 5 & \qquad \REMTEXT{$21$を$16$で割ると「商は$1$」で「あまりは$5$」だ。} \\ 5 \div 8 &=& \underline{0} \REMTEXT{あまり} 5 & \qquad \REMTEXT{$5$を$8$で割ると「商は$0$」で、「あまりは$5$」だ。} \\ 5 \div 4 &=& \underline{1} \REMTEXT{あまり} 1 & \qquad \REMTEXT{$5$を$4$で割ると「商は$1$」で、「あまりは$1$」だ。} \\ 1 \div 2 &=& \underline{0} \REMTEXT{あまり} 1 & \qquad \REMTEXT{$1$を$2$で割ると「商は$0$」で、「あまりは$1$」だ。} \\ 1 \div 1 &=& \underline{1} \REMTEXT{あまり} 0 & \qquad \REMTEXT{$1$を$1$で割ると「商は$1$」で、「あまりは$0$」だ。} \\ \end{array} $$ユーリ「うん? ややこしーなー」
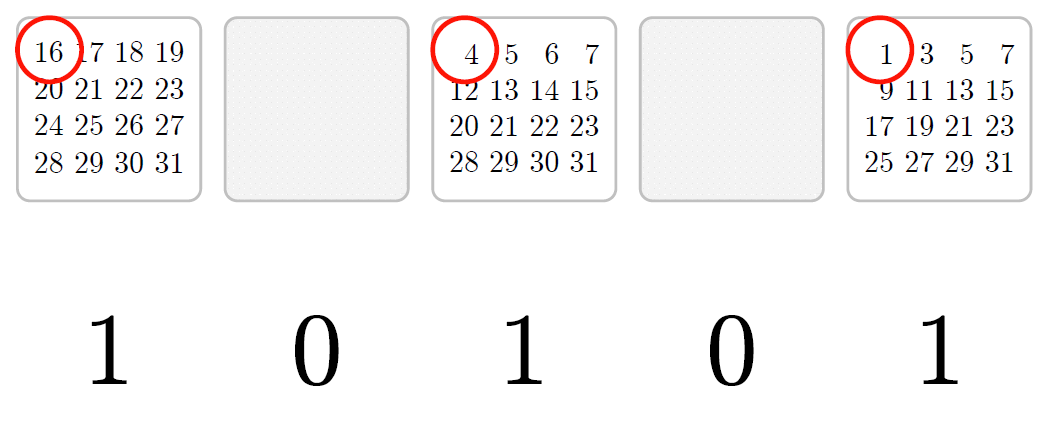
僕「商を上から読んでごらん」
ユーリ「$1, 0, 1, 0, 1$ だけど?」
僕「$21$ をカードで表すと、表、裏、表、裏、表になる。 ちょうどこれは $1, 0, 1, 0, 1$ というパターンに対応する」
《カードの表裏》と《$1$ と $0$》の対応($21$ の例)
ユーリ「おおっ! 計算すればわかるって、そーゆーことか! ユーリ、他の数でやってみる!」
僕「$12$ でやってごらんよ」
ユーリ「うん!」
$$ \begin{array}{rcll} 12 \div 16 &=& 0 \ldots 12 & \qquad \REMTEXT{$12$を$16$で割ると「商は$0$」で、「あまりは$12$」だにゃ。} \\ 12 \div 8 &=& 1 \ldots 4 & \qquad \REMTEXT{$12$を$8$で割ると「商は$1$」で、「あまりは$4$」だにゃ。} \\ 4 \div 4 &=& 1 \ldots 0 & \qquad \REMTEXT{$4$を$4$で割ると「商は$1$」で、「あまりは$0$」だにゃ。} \\ 0 \div 2 &=& 0 \ldots 0 & \qquad \REMTEXT{$0$を$2$で割ると「商は$0$」で、「あまりは$0$」だにゃ。} \\ 0 \div 1 &=& 0 \ldots 0 & \qquad \REMTEXT{$0$を$1$で割ると「商は$0$」で、「あまりは$0$」だにゃ。} \\ \end{array} $$僕「どう?」
ユーリ「うんっ! 商は $0, 1, 1, 0, 0$ になって、 カードの裏、表、表、裏、裏とぴったりだ」
《カードの表裏》と《$1$ と $0$》の対応($12$ の例)

僕「おもしろいだろ?」
ユーリ「うん、おもしろい! けど……なんで商が $1$ になるカードを表にすればいいの?」
僕「たとえば $16$ で割ったときに商が $1$ になるというのはどういうことかを考えればいい。 商が $1$ になるというのは $16$ を $1$ 回だけ引き算できるくらいの大きさだってことだね」
ユーリ「えーと、 $21$ から $16$ は $1$ 回だけ引ける大きさだってこと?」
僕「そうそう。でね、《あまり》っていうのは、これより引き算したらマイナスになっちゃうという残りの数だ」
ユーリ「……」
僕「だから、 $16, 8, 4, 2, 1$ の順番に数を割っていくとき、商が $1$ になるところは、 それぞれ $16, 8, 4, 2, 1$ の数以上だよ、といってるんだ。だから……」
ユーリ「ねえ、お兄ちゃん! 説明とちゅーで悪いんだけど、ユーリ、わかっちゃった」
僕「そう?」
ユーリ「ワニが出てくるんだ!」
僕「ワニ?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2013年2月15日)
この記事は『数学ガールの秘密ノート/整数で遊ぼう』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!