![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/整数で遊ぼう』として書籍化されています。
テトラ「この問題文は、とにかく長いですよね(第13回参照)」
僕「そうだね」
問題文(その1)2013年大学入試センター試験 数学II・数学B 第3問(選択問題)(2)より
正の数からなる数列 $\{ a_n \}$ は、初項から第 $3$ 項が $a_1 = 3, a_2 = 3, a_3 = 3$ であり、すべての自然数 $n$ に対して $$ a_{n+3} = \frac{a_n + a_{n+1}}{a_{n+2}} \qquad \REMTEXT{$\cdots$【2】} $$ を満たすとする。 また、数列 $\{ b_n \}, \{ c_n \}$ を、自然数 $n$ に対して、 $b_n = a_{2n - 1}, c_n = a_{2n}$ で定める。 数列 $\{ b_n \}, \{ c_n \}$ の一般項を求めよう。 まず、【2】から $$ a_4 = \frac{a_1 + a_2}{a_3} = \REMTEXT{[シ]}, a_5 = 3, a_6 = \frac{\REMTEXT{[ス]}}{\REMTEXT{[セ]}}, a_7 = 3 $$ である。 したがって、 $b_1 = b_2 = b_3 = b_4 = 3$ となるので、 $$ b_n = 3 \qquad (n = 1, 2, 3, \ldots) \qquad \REMTEXT{$\cdots$【3】} $$ と推定できる。 【3】を示すためには、 $b_1 = 3$ から、すべての自然数 $n$ に対して $$ b_{n+1} = b_n \qquad \REMTEXT{$\cdots$【4】} $$ であることを示せばよい。このことを……(その2へ続く)
テトラ「でもとにかく[シ]は $2$ で、[ス]は $5$ で、[セ]は $3$ とわかりました(第13回参照)」
僕「うん」
テトラ「でも、困ったのは次の部分です!」
問題文(その2)2013年大学入試センター試験 数学II・数学B 第3問(選択問題)(2)より
(その1から続く)……このことを「まず、 $n = 1$ のとき【4】が成り立つことを示し、 次に、 $n = k$ のとき【4】が成り立つと仮定すると、 $n = k+1$ のときも【4】が成り立つことを示す方法」を用いて証明しよう。 この方法を[ソ]という。 [ソ]に当てはまるものを、次の〔0〕〜〔3〕のうちから一つ選べ。
〔0〕組立除法 〔1〕弧度法 〔2〕数学的帰納法 〔3〕背理法
(問題文はさらに続く)
テトラ「……」
僕「この[ソ]の正解は〔2〕の数学的帰納法になる。 そもそも〔0〕や〔1〕は証明の方法じゃない。 〔3〕の背理法は証明の方法だけど、これは証明したい命題の否定を仮定すると矛盾が導けるという方法で、 自然数の証明とは直接関係はないね」
テトラ「……」
僕「ん? テトラちゃん、どうしたの。背理法のこと、詳しく話す?」
テトラ「い、いえ、そうじゃなくて、あたしはこの問題文の意味がさっぱりわからないんです。 これは……日本語なんでしょうか?」
……「まず、 $n = 1$ のとき【4】が成り立つことを示し、 次に、 $n = k$ のとき【4】が成り立つと仮定すると、 $n = k+1$ のときも【4】が成り立つことを示す方法」……
僕「そうだね、とても日本語には思えない。 ここでも、《少しずつ読む》ことが大事なんだよ。 いいかい、こんなふうに数学的帰納法を《2ステップ》に分けて読んでいこう」
数学的帰納法の《2ステップ》
テトラ「はい……二つのステップに分けました」
僕「ここで僕たちが関心があるのは問題文に出てくる【4】という命題だね」
$$ b_{n+1} = b_n \qquad \REMTEXT{$\cdots$【4】} $$テトラ「はい……ええと、これは数列 $\{ b_n \}$ についての式ですよね?」
僕「そう。《どんな自然数 $n$ についても【4】が成り立つ》ことを証明するのが目標だね。 で、【4】では $n$ という文字がとても重要な役割を果たしているんだよ」
テトラ「はあ……」
僕「【4】は、 $n$ の値が変われば主張していることも変わる式だよね。 たとえば、 $n = 1$ だったら、【4】はこう書ける」
$$ b_{2} = b_1 \qquad \REMTEXT{$\cdots$【4】で$n = 1$の場合} $$テトラ「ははあ……確かにそうですね」
僕「もしも $n = 2$ だったら【4】はどうなるかな?」
テトラ「はい、こうなります」
$$ b_{3} = b_2 \qquad \REMTEXT{$\cdots$【4】で$n = 2$の場合} $$僕「そうそう。で、僕たちが最終的に証明したいのは、 $n=1$ でも、 $n=2$ でも、 $n=3$ でも、……どんな自然数 $n$ に対しても、【4】が成り立つということなんだ」
テトラ「はい! でも……自然数は無数にあるんですよね。それが大問題です」
僕「うん、そうだね。 自然数は無数にある。 それは確かに大問題だ。 $b_2 = b_1$ を証明し、 $b_3 = b_2$ を証明し、……というふうにすべてをひとつひとつ証明していくわけにはいかない。 自然数は無数にあるんだから、いくらひとつひとつ証明していっても証明し尽くすことができないし」
テトラ「そうですそうです! 証明し尽くすことができない——それです!」
テトラちゃんは興奮してぶんぶんと頷く。
僕「そこで、数学的帰納法の登場だよ。さっきの《2ステップ》をもう一度よく見てみよう」
数学的帰納法の《2ステップ》
僕「ステップAは《$n = 1$ のとき【4】が成り立つことを示す》というものだけど、 これは、いったい何を言ってるか、テトラちゃん、わかる?」
テトラ「え……あの……」
僕「テトラちゃんはもうわかっていると思うよ」
テトラ「えっと、まちがっていたらすみません。《$n = 1$ のとき【4】が成り立つことを示す》っていうのは、 《$b_2 = b_1$ を示す》っていうこと……かなあ……と」
僕「そうそう、それでいいんだよ」
テトラ「ああ、よかったです。でも、あの、こんなこと言ってはなんですけれど、《それだけのこと?》って思っちゃいます。 《まず、 $n = 1$ のとき……》なんて、ちょっと、大げさですよね?」
テトラちゃんが大きな目で僕を見る。
僕「そうだね。やっていることに比べて確かに大げさな言い方かもしれない。 でもそれは、問題作成者が、数学的帰納法の形に合わせようとしているからだと思うな。 つまり、数学的帰納法の形を知っている人にわかりやすいようにするために、 かえって大げさな言い方になってしまってるんだね」
テトラ「数学的帰納法のカタチですか……」
僕「ところで、 $b_2 = b_1$ は実際のところ、成り立つかな。テトラちゃんは $b_2 = b_1$ を証明できる?」
テトラ「え? ええっと……証明はできませんけど、 $b_1 = 3$ と $b_2 = 3$ をさきほど求めました(第13回参照)から、 $b_2 = b_1$ は成り立つといえる……と思います」
僕「その通り! それで立派な証明だよ、テトラちゃん」
テトラ「そうなんですか。……証明って何か、こう、難しい数式を使わなくちゃいけないと思っていました。そうじゃないんですね」
僕「うん。難しい数式を使わなくちゃいけないなんてルールはないよ。 $b_2$ と $b_1$ の両方とも $3$ という数に等しい。だから、 $b_2 = b_1$ であるといえる。 これは立派な証明になってる」
テトラ「はい、わかりました」
僕「では、次に《2ステップ》のステップBをよく見てみよう。ここが数学的帰納法の核心になる」
数学的帰納法の《2ステップ》
テトラ「このステップBは、とても日本語に見えません! それに、 $n = k$ と言ってるのに、 すぐ後で $n = k+1$ だなんて……これは成り立たないですよね」
僕「あ、そう読むんじゃないんだよ。そういう読み方はテトラちゃんらしくないなあ。 数式だけに気を取られているね。ステップBもまた、少しずつ読むために区切ってみよう」
テトラ「少しずつ読むのは大事なんですね」
ステップBを区切って読む
次に、
$n = k$ のとき【4】が成り立つ
と仮定すると、
$n = k+1$ のときも【4】が成り立つ
ことを示す
テトラ「あ、そう……なんですね」
僕「こんなふうに区切って読むと、重要な二つの主張が出てきていることがわかると思う。 つまり、《$n = k$ のとき【4】が成り立つ》と《$n = k+1$ のときも【4】が成り立つ》だ。 いい? 《$k$ のとき》と《$k+1$ のとき》が重要だよ」
テトラ「はあ、確かに、その二つが出てますが……」
僕「思い切って肉を削って《2ステップ》の骨組みだけ書いてみると、もっとはっきりするよ」
数学的帰納法の《2ステップ》の骨組み
テトラ「す、すみません。あたし、わかりません……」
僕に向かって、テトラちゃんがもうしわけなさそうな表情を見せる。 僕はどうしたらテトラちゃんにわかってもらえそうか、頭をめぐらせる。
僕「うん、そうだ! ドミノ倒しみたいなものだと考えるといいよ」
テトラ「あの、ひとつ倒すとパタパタパタ……と倒れていくドミノ倒しですか」
僕「そうそう、それそれ。ステップAを、《$1$ 番目のドミノを倒せる》と読む」
ステップA:《$1$ 番目のドミノを倒せる》

テトラ「はあ」
僕「そしてステップBを、どんな自然数 $k$ に対しても《$k$ 番目のドミノが倒れたならば、 $k+1$ 番目のドミノも倒れる》と読む」
ステップB:どんな自然数 $k$ に対しても《$k$ 番目のドミノが倒れたならば、 $k+1$ 番目のドミノも倒れる》
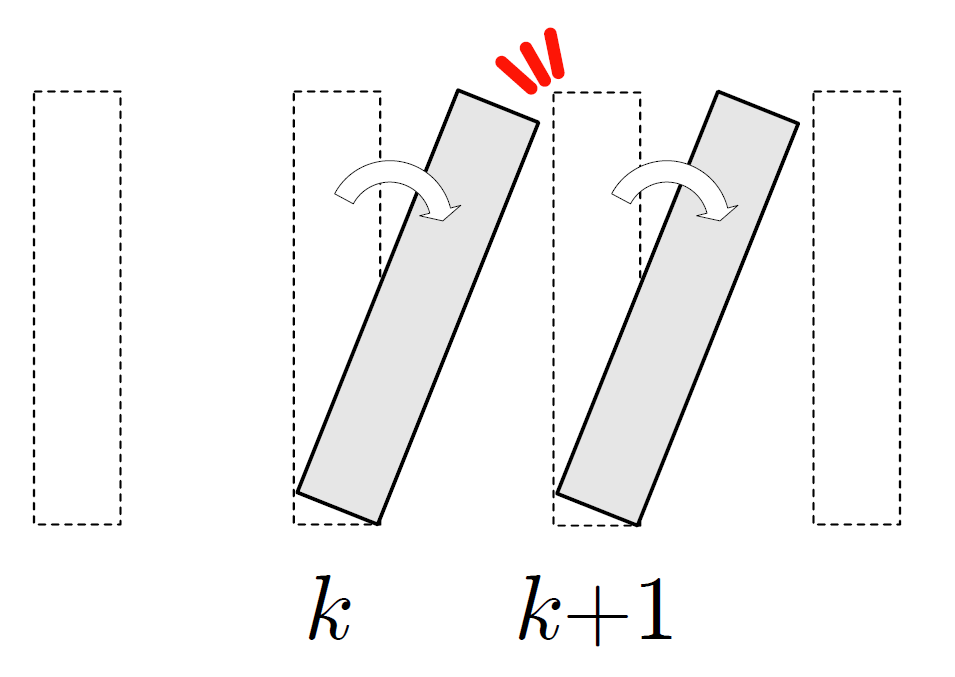
テトラ「次のドミノがパタンと倒れるということですね」
僕「そうだよ。 この二つのステップAとBが両方成り立つなら……どんなに大きな自然数 $n$ 番目のドミノも倒れる と証明できたことになる。 たとえば、 $100$ 番目のドミノでも倒れるといえるよね」
$100$ 番目のドミノも倒れるといえる
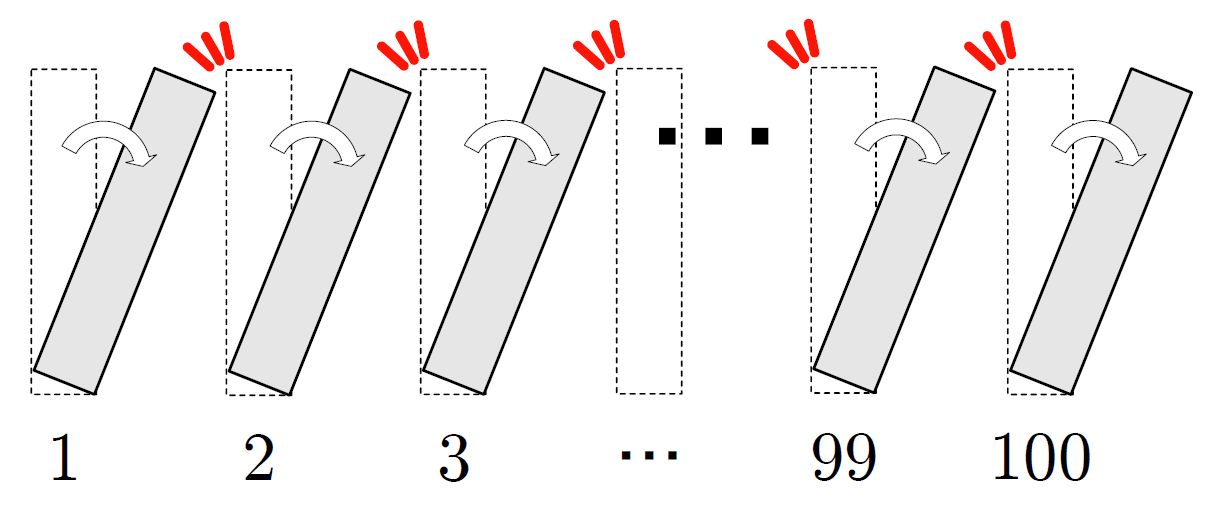
テトラ「ははあ……なんとなくわかってきました。確かにそれはそうですね」
僕「そうそう、そういうことだよ。これが数学的帰納法という証明の方法に通じるんだ」
テトラ「あっ、先輩、先輩! わかってきましたよっ! 《ドミノが倒れる》は《【4】が成り立つ》の《たとえ話》になってるんですね!」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2013年2月1日)
この記事は『数学ガールの秘密ノート/整数で遊ぼう』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!