![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/整数で遊ぼう』として書籍化されています。
僕は高校二年生、ユーリは中学二年生。 $0$ 以上の整数 $N$ について 《$N$ の各桁の数字をすべて加えた数は $3$ の倍数である》が《$N$ は $3$ の倍数である》ことの判定法であることを証明していた(第11回参照)。
僕「これで、 $3$ 桁の場合の証明ができたよね」
ユーリ「うん、まーね」
僕「これを、さらに一般化してみよう。数学がおもしろくなるのはここからだよ。いいかい、 $n$ という文字を導入して……」
ユーリ「ちょっと待って、お兄ちゃん」
僕「がく。どうした?」
ユーリ「あのね、お兄ちゃんはいま、 $N$ が $3$ 桁の場合を証明してくれたじゃん?」
僕「うん」
ユーリ「そんとき、数式を使ったよね」
僕「そうだよ。 $N = 100a + 10b + c$ とおいたけど?」
ユーリ「でもね、もっと、ずっと、簡単にできそーだ! ってひらめいたの」
僕「へえ! どういうひらめき?」
ユーリは栗色のポニーテールを揺らして熱心に話し出す。
ユーリ「あのね、《$N$ の各桁を足したのが $3$ の倍数》かどうかで《$N$ は $3$ の倍数》かどうかを判定したいんでしょ?」
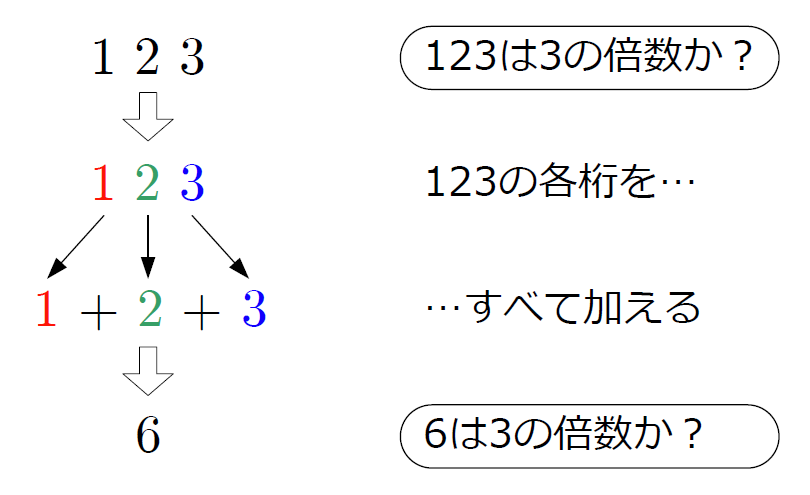
僕「そうだよ、それでいい」
ユーリ「$0$ は $3$ の倍数じゃん? そこに $1$ ずつ足してくんだよ。 そーすると、倍数→違う→違う→倍数→違う→違う→倍数→……ってなるの。 どっちもそーなの」
僕「え? ちょっとよくわからないな。ユーリは何を言いたいの? 倍数・違う・違う……って何?」
ユーリ「$0$ は $3$ の倍数だよね。《倍数》」
僕「そうだよ」
ユーリ「$1$ は $3$ の倍数じゃない。《違う》」
僕「うん」
ユーリ「$2$ も $3$ の倍数じゃない。《違う》……ね?」
僕「ああ、そういうこと? $3$ の倍数が $3$ つごとに出てくるって言いたいんだね」
ユーリ「だから、そー言ってんじゃん!」
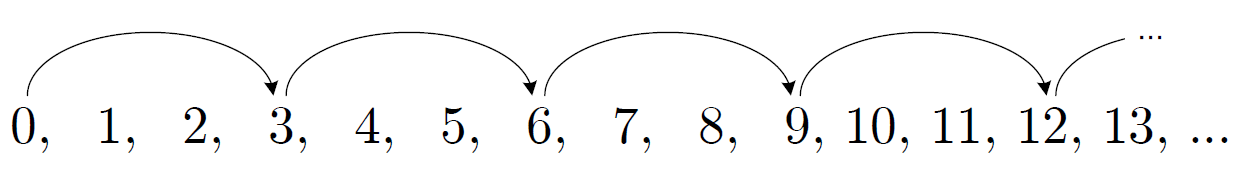
僕「それがどうしたの? いま考えているのは《$3$ の倍数の判定法》だよ」
ユーリ「だーかーらー! それをいま説明してんじゃん! ちゃんと聞いてよ。 $3$ の倍数はどっちも $3$ つごとなの! でね、足し算の方はね、 位上がりのところが $9$ でうまくいくから大丈夫なの。 一の位に $1$ を乗せるか、十の位に $1$ を乗せるかの違いだもん。 だから、ほらね。証明できた」
僕「何が? ごめん、ユーリ。何を言いたいのかわからないよ」
ユーリ「えー! なんでお兄ちゃん、わかってくんないの? お兄ちゃん、嫌いっ!」
大声を出すユーリ。 めずらしく涙目になっていて、僕はあわてた。
ふだん、僕はユーリの話をかなり根気よく聞く方だと思う。 それから、彼女の説明したいことも、先取りして理解しているつもりだ。 でも、今回はまだよくわからない。
いま考えたいことは、 《$N$ の各桁をすべて加えた数は $3$ の倍数である》が《$N$ は $3$ の倍数である》の判定法だということなんだけれど……。
ユーリはいったい何を考えてるんだろう。
僕「ねえ、ユーリ。ちゃんと聞くから、もう少しゆっくり説明してくれるかなあ」
ユーリはしばらくムッとしていたけれど、しぶしぶ話し出した。
ユーリ「……あのね、ユーリは $0$ から順に考えることにしたの。 お兄ちゃんは数式を使って証明してくれたけど、 なんだかね、それがややこしいと思ったから。 だって $3$ の倍数ってもっと簡単じゃん? だからバシッとできると思ったの」
僕「うん、それで?」
ユーリ「$0$ は $3$ の倍数だし、 $1$ は $3$ の倍数じゃないし、 $2$ は $3$ の倍数じゃないし、 $3$ は $3$ の倍数でしょ?」
僕「うん、いいよ」
ユーリ「それでね、 $0,1,2,3,4,\ldots$ みたいにね、順に考えていくの。 そうすると、 $3$ つごとに $3$ の倍数になるわけでしょ?」
$$ \underline{0}, 1, 2, \underline{3}, 4, 5, \underline{6}, 7, 8, \underline{9}, 10, 11, \underline{12}, 13, \ldots $$僕「その通りだよ。 $N$ を $1$ ずつ増やしていくと、 $3$ つごとに $3$ の倍数になる」
ユーリ「でね、もしもさ、数がヒトケタなら《いえる》じゃん?」
僕「《いえる》って……何が?」
ユーリ「あーもー! 《各桁を足したのが $3$ の倍数になるかどうか》が 《全体も $3$ の倍数になるかどうか》の判定法だ——そう《いえる》でしょ! ヒトケタなら!」
僕「あ、そうだね。確かに《いえる》。 数が一桁($0,1,2,3,4,5,6,7,8,9$)なら当たり前だね。各桁といっても数字一つなんだから」
$3$ の倍数の判定法(一桁の場合)
数 $N$ が一桁のとき、
《$N$ の各桁を足した数は $3$ の倍数である》は、
《$N$ は $3$ の倍数である》ことの判定法になっている。
ユーリ「だからさー、問題は位が上がるときだけなの。位上がりについて気をつければいーんだよ!」
僕「お。ユーリが言いたいことがわかってきたぞ」
ユーリ「位上がりが起きるのは《$9$ に $1$ 足したときだけ》でしょ? そんときはね、 《一の位に $1$ を乗せる》か《十の位に $1$ を乗せるか》の違いだけだからいいの。《$9$ はつぶれてもいい》し!」
僕「その《$1$ を乗せる》と《$9$ はつぶれてもいい》って何のこと?」
ユーリ「あーもー! にぶいにゃあ! こういうこと!」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2013年1月18日)
この記事は『数学ガールの秘密ノート/整数で遊ぼう』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!