![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/整数で遊ぼう』として書籍化されています。
ユーリ「お兄ちゃん、クイズ出したげるよ」
僕「その《たげる》は何?」
ユーリ「まーいいじゃん。あのね、 一億二千三百四十五万六千七百八十九は《$3$ の倍数》かにゃ?」
問題
一億二千三百四十五万六千七百八十九は《$3$ の倍数》か。
ユーリはいきなり猫語で質問を繰り出してくる。 ユーリは中学二年生。僕の従妹だ。 小さい頃からいっしょに遊んでいたから、 高校二年生の僕のことをいつも《お兄ちゃん》と呼ぶ。 僕の部屋に遊びに来ては本を読んだり、クイズをしたり……
僕「ん? 要するに $123456789$ ってこと?」
ユーリ「そーそー。さーどーだ!」
僕「$3$ の倍数かどうかだろ? 簡単だよ。 $123456789$ は $3$ の倍数だ」
ユーリ「ちぇー、つまんないの。お兄ちゃん、即答しないでよ」
解答
一億二千三百四十五万六千七百八十九は《$3$ の倍数》である。
僕「こんなの基本だよ。《$3$ の倍数かどうか》を知りたかったら、 《各桁の数字をすべて足し合わて $3$ の倍数になるかどうか》を調べればいい、簡単」
$3$ の倍数かどうかを調べる方法
《$3$ の倍数かどうか》を調べるには、 《各桁の数字をすべて足し合わせて $3$ の倍数になるかどうか》を調べる。
たとえば、 $123456789$ の各桁の数字をすべて足し合わせると、 $$ 1+2+3+4+5+6+7+8+9 = 45 $$ となる。 $45$ は $3$ の倍数だから、 $123456789$ も $3$ の倍数になる。
ユーリ「ちぇっ、やっぱり知ってたか」
僕「ユーリ。最近、言葉使いが乱暴になってないか?」
ユーリ「そんなことないですよー。ちゃーんとわきまえてございますもん」
僕「日本語へんだぞ」
ユーリ「でも、お兄ちゃん、暗算早いよね。 $1+2+3+4+5+6+7+8+9$ をそんなに早く計算できるの?」
僕「ん? いや、覚えてたから」
ユーリ「へ?」
僕「$1$ から $10$ まで足した数は $55$ になるって、暗記してるから。 $55$ から $10$ を引いて $45$ だろ? だから $1+2+3+4+5+6+7+8+9=45$」
ユーリ「なにそのマニアックな発言」
僕「マニアックじゃないって……ところで何で急に $123456789$ のクイズが出てきたんだ?」
ユーリ「あのね、授業でその話が出たから。 $3$ の倍数の話。へーって思ったの」
僕「そうか……あれ? ところでユーリは自分では納得してるの?」
ユーリ「納得ってどーゆーこと?」
僕「自分で《確かにそうだ》と確認したかどうかだよ。 《各桁をぜんぶ足して $3$ の倍数になるかどうか》っていうのは、 有名な $3$ の倍数の判定方法だけど、 どうしてこのやり方でいいのか、納得してる?」
ユーリ「え……」
ユーリは困った表情になってポニーテールの髪をいじりだした。
僕「《各桁をぜんぶ足して $3$ の倍数になるかどうか》が $3$ の倍数の判定方法になることは、 きちんと数学的に証明できるよ。中学生でも大丈夫」
ユーリ「《しょーめい》って何?」
僕「数学の証明っていうのは、 与えられた条件から、ある数学的な主張までの道筋を論理的に示すことだよ。 《たぶんこうなんじゃないかな》や《経験上こうなんだよ》じゃなくて、 《論理的に絶対これが成り立つ》と示すことが証明だね」
ユーリ「ほー! 論理的に絶対って? ユーリ、証明、好きかも!」
僕「きっと好きだと思うよ」
ユーリは《バシっとわかる》のが好きだからな。
ユーリ「証明ってどうするの?」
僕「話を《$3$ 桁の正の整数》にしぼって考えることにしよう」
証明したいこと
$N$ は $3$ 桁の正の整数とする($N = 100, 101, 102, \ldots, 999$)。
$N$ の各桁の数字をすべて足した数が $3$ の倍数ならば、 $N$ は $3$ の倍数である。
ユーリ「ふーん」
僕「いや、ふーん、じゃなくて、これを証明するんだよ」
ユーリ「わかんない。ねー、お兄ちゃん。なんでこんなややこしい話になっちゃうの? $N$ とか出てきてやだな」
僕「$N$ が出てくるのは、問題の内容が正確に伝わるようにするためだよ」
ユーリ「あのね、たとえば $123$ とか考えちゃだめなの?」
僕「もちろんいいよ。具体的な数で考えたいんだね。それはとても大事なことだ」
ユーリ「たとえばね、 $123$ という数だと、 $1 + 2 + 3 = 6$ で、 $6$ は $3$ の倍数。 それから $123$ は $3$ で割ると…えーと… $41$ かにゃ? うん、 $123 \div 3 = 41$ で割り切れる。オッケー! いいじゃん」
僕「……うん、ユーリはいま、 《$N$ の各桁の数字をすべて足した数が $3$ の倍数ならば、 $N$ は $3$ の倍数である。》 を、具体的な $N = 123$ について確かめたんだね」
ユーリ「ま、そーだよー」
僕「それは正しいし、いま問題になっていることの具体例になっている。 《例示は理解の試金石》だ。ユーリは問題の中心的なアイディアをよく理解しているといえる」
ユーリ「えへん」
僕「でもね」
ユーリ「?」
僕「いまやりたいのは、そこからもう一歩進むことだよ。 つまり、もっと《一般的なこと》を証明したいんだ」
ユーリ「一般的なこと?」
僕「そう。 ユーリは $N = 123$ という具体的な数で調べた。 でも $N = 100, 101, 102, \ldots, 999$ のように $3$ 桁の数すべてについて 確かめるわけにはいかないよね」
ユーリ「なんで? $124$ でも $567$ でも $999$ でも、確かめられるよ?」
僕「わかった、お兄ちゃんの言い方が悪かった。 確かめることはできる。でも、とても手間がかかるんだ。 $100$ から $999$ までの数一つ一つを調べていくのは不可能じゃない。でも、手間がかかる」
ユーリ「ふんふん。まー、めんどーだよね」
僕「具体的に一つ一つ調べるのに手間がかかるとき、数学では文字を使うことがある」
ユーリ「文字を使う? 数学の問題なのに?」
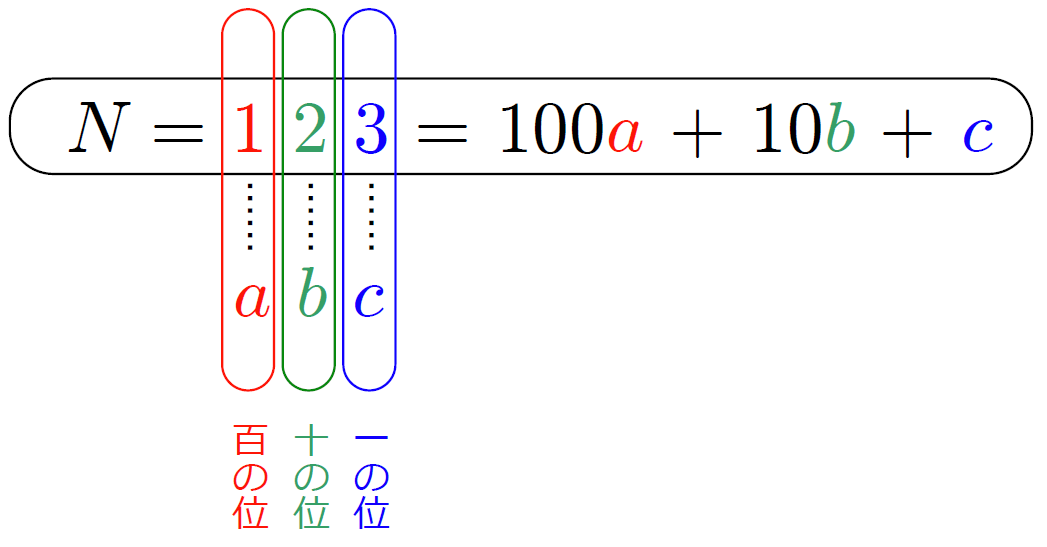
僕「そう。《文字の導入による一般化》というんだよ。 $3$ 桁の正の整数 $N$ は、 $a,b,c$ という文字を使って次のように書ける」
《$3$ 桁の正の整数 $N$》を文字 $a,b,c$ を使って書く。
$$ N = 100a + 10b + c $$
ただし、 $a,b,c$ はそれぞれ、
$a = 1,2,3,4,5,6,7,8,9$(のいずれか)
$b = 0,1,2,3,4,5,6,7,8,9$(のいずれか)
$c = 0,1,2,3,4,5,6,7,8,9$(のいずれか)
とする。
ユーリ「出たな数式マニア」
僕「マニアというほどの数式じゃないよ。 $100a + 10b + c$ という数式を、 掛け算の記号を使って書ける?」
ユーリ「書けるよー。こうでしょ?」
$$ 100 \times a + 10 \times b + c $$僕「そうそう。《$100$ 倍した $a$ と、 $10$ 倍した $b$ と、 $c$ を足した数》を表している」
ユーリ「ねー、でも、この $a$ って何?」
僕「それはとてもいい疑問だよ、ユーリ。 いま $a,b,c$ は $3$ 桁の数の各桁を表している。 $a$ は百の位の数字、 $b$ は十の位の数字、 $c$ は一の位の数字だよ」
ユーリ「どーして?」
僕「え、どーしてって?」
ユーリ「どーして、そんなことがわかるの? $a$ が百の位とかさ」
僕「あ、そうじゃない、そうじゃない。 あのね、 $a$ を百の位の数字、 $b$ を十の位の数字、 $c$ を一の位の数字を表すと決めたのはお兄ちゃんなんだよ。 いま、そういうふうに自分で決めたんだ。 これからの証明のために自分で定義したんだよ」
ユーリ「そーゆーのって自分で勝手に決めてもいーの?」
僕「うん、いいんだよ。自由に定義していい。 そうか、ユーリは数式を使って考えるのにあまり慣れていないんだね。 数式を使って考えを進めるとき、自分の考えを進めやすいように、 自分で文字を定義することはとても大切なんだ。 文字は自由に選べる。お兄ちゃんはいま $a,b,c$ という文字を選んだけれど、 他の文字を使ってもいい」
ユーリ「ふんふん」
僕「どんな文字を使ってもいいけど、その文字が何を表しているかは、はっきりさせておかなくちゃいけない。 文字が何を表すかをはっきりさせないと、わけがわからなくなるから」
ユーリ「そりゃそーだ」
僕「話を戻そう。いま $3$ 桁の正の整数 $N$ を、 $$ N = 100a + 10b + c $$ と表して、 $N$ の百の位の数字、十の位の数字、一の位の数字をそれぞれ $a,b,c$ で表すものとしよう。 そのようにお兄ちゃんが定義したということだよ」
ユーリ「うん、わかった!」
僕「$N = 123$ のとき、 $a$ は具体的に何になると思う?」
ユーリ「へ? 百の位だから $100$ じゃないの?」
僕「違うよ。 $a$ は $100$ じゃなくて $1$ だ」
ユーリ「あ、そーか。じゃあ、 $a$ は $1$ から $9$ までのどれか?」
僕「その通り。 $a$ は $1,2,3,\ldots,9$ のどれか。 $b$ と $c$ も似ているけれど、 $0$ になる場合がある」
ユーリ「そっか。 $3$ 桁だから $a$ だけ $0$ にならないんだね」
僕「そうそう。いいぞ」
ユーリ「ねー、お兄ちゃん。これって $3$ の倍数かどうかに関係しているの?」
僕「まだ下ごしらえ。関係するのはこれからだね」
ユーリ「むー」
僕「これで $N$ が $N = 100a + 10b + c$ で表せるっていうのはいいよね」
ユーリ「だいじょーぶ」
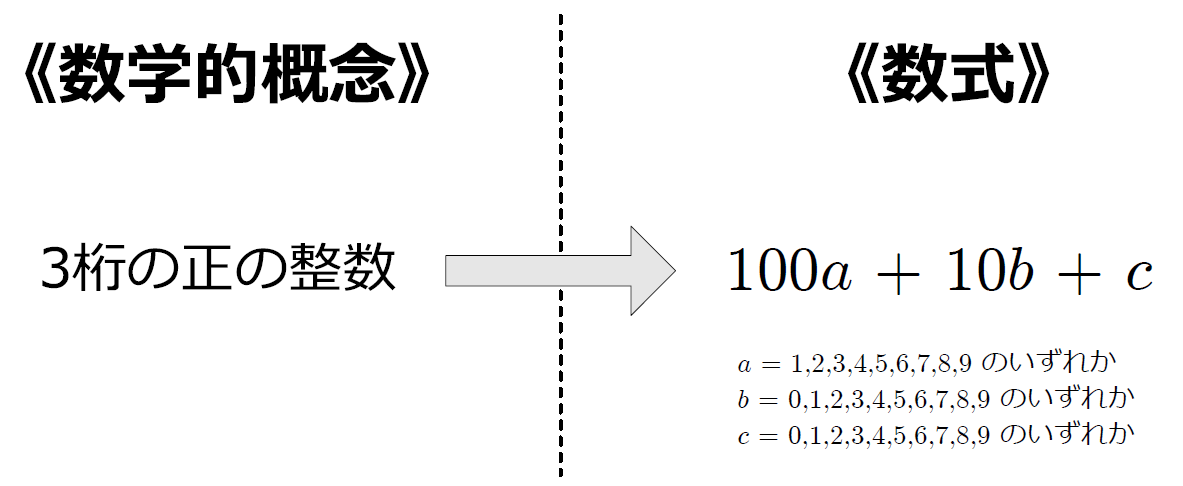
僕「よしよし。ここまでで、 $N$ を $100a + 10b + c$ と表すという数学のやり方に慣れたよね。 これは《数学的概念を数式で表す》という練習になってるんだよ」
ユーリ「ごめん、すーがくてき……なに?」
僕「数学的概念を数式で表す。 《数学的概念》っていうのは、《$3$ の倍数》や《$3$ 桁の正の整数》のような数学的な《何か》のことをちょっと気取って呼んだんだよ。 数学で証明をするときにはね、自分の頭の中にある《数学的概念》を《数式》で表すことがよくあるんだ。 まあ、自分が考えたことを数式にするってこと」
ユーリ「すーがくてきがいねん……」
僕「いまは《$3$ 桁の数》という数学的概念を数式で表したい。 そのために、各桁の数字を表す文字 $a,b,c$ を導入した。 それで《$3$ 桁の数》は《$100a + 10b + c$》という数式で書けたよね」
ユーリ「すーがくてきがいねん……って、なんかカッコイイね、お兄ちゃん」
ユーリの栗色の髪がきらっと金色に輝いた。
僕「そうだね。 $N$ や $a,b,c$ のような文字が何を表しているのかわからないと、 数式は難しく感じちゃう。 でもね、ひとつひとつの文字が何を表しているかを落ち着いて理解すれば、 数式なんて少しも恐くはないんだよ」
ユーリ「ねえ! ユーリは《数式が恐い》なんて言ったことないよ! ただ、ちょっと、めんどいな——って思っただけじゃん!」
僕「そうだっけ」
ユーリ「あ! これって、お兄ちゃんがこないだ話してくれたツルカメ算! 《現実の世界》と《数学の世界》の話だ!(第4回参照)」
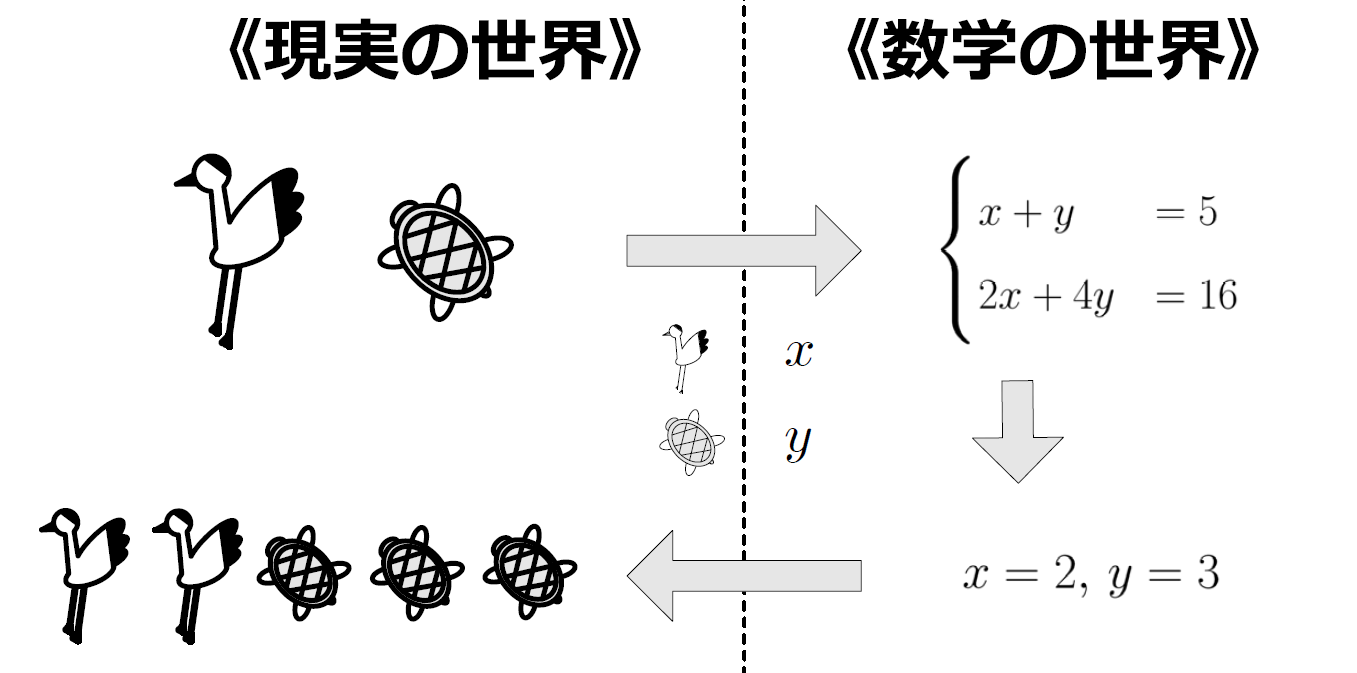
僕「ああ、そうだったね。 《現実の世界》を《数学の世界》に移す。 《数学的概念》を《数式》で表す。うん、似たような話だよ」
ユーリ「それで、ここからどーするの? 証明すんでしょ?」
僕「次にやりたいのはね、 $N$ を $100a + 10b + c$ と書いたとき、 《$N$ の各桁の数字をすべて加えた数》という数学的概念を数式で表したい。できる?」
ユーリ「にゃるほど。《$N$ の各桁の数字をすべて加えた数》……って簡単じゃん! $a + b + c$ だよ!」
《$N$ の各桁の数字をすべて加えた数》を数式で表す。
$$ a + b + c $$
僕「その通り! 僕たちは $a,b,c$ がそれぞれ各桁の数を表しているって定義した。 だから、《各桁の数をすべて加えた数》は、 $a + b + c$ という数式で表せる」
ユーリ「へへん、数式なんて簡単じゃ」
僕「いきなり年を取るなよ」
ユーリ「それでそれで? 次は?」
僕「次は、ちょっと難しいぞ。 《$N$ の各桁の数字をすべて加えた数は $3$ の倍数である。》を数式で表してみよう。 《$3$ の倍数である》はどう書けるかな」
ユーリ「簡単だよ! こうだね!」
$$ a + b + c = \REMTEXT{《$3$の倍数》} \qquad \REMTEXT{(?)} $$僕「ええっとね、ユーリ。方向性は合ってる。 でも、もう一息。この等式の右辺の《$3$ の倍数》も数式で書いてほしい」
ユーリ「んんん?」
僕「こんなふうにすればいいよ」
《$N$ の各桁の数字をすべて加えた数は $3$ の倍数である》を数式で表す。
$$ a + b + c = 3d $$
ただし $d$ は $0$ 以上の整数とする。
ユーリ「$d$ なんて新しい文字使っていいの?」
僕「もちろん」
ユーリ「$d$ って何なの?」
僕「$d$ は、 $a + b + c$ を $3$ で割った答え(商)になるけど、 $d$ が具体的に何になるかは、 $a,b,c$ が決まらなければわからない」
ユーリ「ねー、お兄ちゃん。文字を使うとわかりにくくなるみたい。だって、 $a,b,c,d$ のどれもわからなくて……」
僕「うん、確かにそう感じてもしょうがない。 文字を使うと、具体的な数が見えなくなっちゃうからね。 具体的じゃないと、わかりにくい。でもその代わり、いいこともあるんだよ」
ユーリ「いいこと?」
僕「文字を使うと、具体的な数が見えなくなる。 でも、その代わり、文字を使うとたくさんの数を一度に扱うことができるんだよ。 それが、まさに、文字を使って一般的に考えるってことなんだ」
ユーリ「一般的に考える?」
僕「そう。たくさんの数を一度に扱えるってことだよ」
ユーリ「ふーん……」
僕「ここまでいっしょに考えてきたことをまとめてみよう」
ユーリ「うん、そこまではわかった。完璧だよ」
僕「これから僕たちが証明したいことは何だっけ」
ユーリ「何だっけ」
僕「《$N$ の各桁の数字をすべて加えた数は $3$ の倍数である》ならば、《$N$ は $3$ の倍数である》ということを証明したい」
証明したいこと
《$N$ の各桁の数字をすべて加えた数は $3$ の倍数である》ならば、《$N$ は $3$ の倍数である》
ユーリ「うん。そうだった」
僕「それじゃあね、《$N$ は $3$ の倍数である》は数式で書ける?」
ユーリ「わかんな……くない! さっき似たようなことやった。わかった、こうかにゃ?」
$$ N = 3d \qquad \REMTEXT{(?)} $$僕「惜しい!」
ユーリ「え? だって $3$ の倍数は $3d$ なんでしょ?」
僕「そうなんだけど、 $d$ という文字はさっき別の意味で使ったから、今度は別の文字 $e$ を使おう」
ユーリ「あ、そっか」
《$N$ は $3$ の倍数である》を数式で書く。
$$ N = 3e $$
ただし $e$ は $0$ 以上の整数とする。
僕「$N = 100a + 10b + c$ だから、こう書いてもいいよ」
《$100a + 10b + c$ は $3$ の倍数である》を数式で書く。
$$ 100a + 10b + c = 3e $$
ただし $e$ は $0$ 以上の整数とする。
ユーリ「えーっと、そっか、うん、わかった」
僕「ここまでずっと、数学的概念を数式であらわそうとしてきたけど、 僕たちが証明したいことっていうのは、こうなる」
証明したいことを数式を使って書く。
《$a + b + c = 3d$》ならば、《$100a + 10b + c = 3e$》である。
ユーリ「ほーほー」
僕「ここまで整理ができたなら、数式の力を信じて進むことができる。 $100a + 10b + c$ という式を何とかして $3e$ という形に変形すればいいから。これが《目標の形》」
$100a + 10b + c$ を《目標の形($3e$)》に変形したい!
$$ N = 100a + 10b + c = \,\stackrel{\REMTEXT{?}}{\cdots}\, = 3e $$
ただし、 $e$ は $0$ 以上の整数である。
ユーリ「ふーん……」
僕「数式を $3e$ という形にもっていくぞ! という気持ちを持つわけだね。がんばるぞ、おー!」
ユーリ「おー!」
僕「あとは数式の変形で進める」
$$ \begin{array}{rcll} N &=& 100a + 10b + c & \\ &=& (99a + a) + 10b + c & \REMTEXT{$100a$を$99a + a$にした} \\ &=& (99a + a) + (9b + b) + c & \REMTEXT{$10b$を$9b + b$にした} \\ &=& 99a + 9b + (a + b + c) & \REMTEXT{足し算の順序を変えた} \\ &=& 99a + 9b + 3d & \REMTEXT{$a+b+c = 3d$だから} \\ &=& 3 \times 33a + 9b + 3d & \REMTEXT{$99 = 3 \times 33$だから} \\ &=& 3 \times 33a + 3 \times 3b + 3d & \REMTEXT{$9 = 3 \times 3$だから} \\ &=& 3(33a + 3b + d) & \REMTEXT{$3$でくくる} \\ &=& 3e & \REMTEXT{$e = 33a + 3b + d$とおいた} \\ N &=& 3e & \REMTEXT{結局、これが得られた} \\ \end{array} $$僕「さあ、どうかな!」
ユーリ「ややこしー……なんで急に $99$ とか出てくるの?」
僕「$99$ や $9$ は $3$ の倍数だからだよ。最後に《$3$ でくくる》ってやりたかったんだ」
ユーリ「あ、そーゆー作戦か」
僕「数式を $\cdots = 3e$ という形にもっていくぞ! って言ったじゃないか」
ユーリ「そーだった」
僕「$3$ でくくった $3(33a + 3b + d)$ という式で、 $33a + 3b + d$ は $0$ 以上の整数になるから、 $e = 33a + 3b + d$ とおける。 だから結局、 $$ N = 100a + 10b + c = \cdots = 3e $$ が成り立った。 そして、これが証明したかったことだ」
ユーリ「……」
僕「これで証明できた。 各桁の数字の $a,b,c$ をすべて加えた数が $3$ の倍数になるなら、 全体の $N$ も $3$ の倍数になるといえた!」
証明できたこと
$N$ は $3$ 桁の正の整数だとする($N = 100, 101, 102, \ldots, 999$)。
$N$ の各桁の数字をすべて加えた数が $3$ の倍数ならば、 $N$ は $3$ の倍数である。
ユーリ「……」
僕「お、何だかノリが悪いな」
ユーリ「あのね、お兄ちゃん。 お兄ちゃんが見せてくれた証明はわかったよ。リクツもちゃんとわかったけど……」
僕「けど?」
ユーリ「うーん。うまくいえない。お兄ちゃんの言ってた《証明したいこと》が……」
僕「気になる?」
ユーリ「……ま、いっか。とにかく数式がめんどいのは確かだよね」
僕「まあね。でも、よく考えてごらん。 $100,101,102,\ldots,999$ っていうたくさんの数をひとつひとつ調べる必要はもうないんだ。 $100a + 10b + c$ という数式を一つ調べるだけで、 ぜんぶ調べた代わりになるんだから」
ユーリ「そっか。それは便利」
僕「うん、ここから、さらに一般化することもできるよ。もう一歩を進めよう」
ユーリ「もう一歩?」
僕「そう。いまは $3$ 桁で考えてきたけれど……」
この記事は期間限定で「ただいま無料」となっています。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(第11回終わり)
(2013年1月11日)
この記事は『数学ガールの秘密ノート/整数で遊ぼう』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!