第10回 シーズン1 エピソード10

交わる点、接する点（後編）

図書室にて

僕「さて、ここまで放物線と $x$ 軸の話をしてきたけれど、今度は、交点（こうてん）について考えてみようか」

テトラ「交点……ですか」

僕「うん。放物線と $x$ 軸の交点は、二つの図形が交わっている点だよね」

テトラ「そうですね」

僕「で、交点という言い方は《図形の世界》の表現になるわけだ。それに対して——」

ミルカ「楽しそうだな」

テトラ「あ、ミルカさん！」

僕「いま放物線と $x$ 軸の話をしていたんだよ」

ミルカ「ふうん？」

テトラ「あ、あの……放物線を移動するときのお話がまだきちんとわかっていなくて」

ミルカ「ああ、 $2$ 次式の話か」

僕「そうだよ、ミルカさん。いま、ちょうどその話をしようと思っていたところなんだ」

ミルカ「続ければ」

ミルカさんはそう言って、向かい側の席で本を読み始めた。 僕はなぜか少し緊張しつつテトラちゃんへの説明を再開する。

僕「放物線 $y=x^2-2x$ の上には無数の点があるよね」

テトラ「はい、そうですね」

テトラちゃんは、手でぶんっと放物線を描いた。

僕「その放物線上にある点を $(x,y)$ で表すと、 $x$ と $y$ にはルールがある」

テトラ「はい、そうでした。必ず $y=x^2-2x$ が成り立っているんですよね」

僕「そうそう。それから、 $x$ 軸の上にも無数の点 $(x,y)$ があって、その $x$ と $y$ にもルールがある」

テトラ「はいはい。大丈夫です。必ず $y=0$ が成り立っているということですね。 $x$ と $y$ のルールです——って、 $x$ は出てきませんけれど」

僕「うん、それでいい。いまから、この二つの図形が交わってできる点を考えたい。つまり、交点（こうてん）を考えるということ」

テトラ「はい。ここと、ここにある点のことですねっ！」

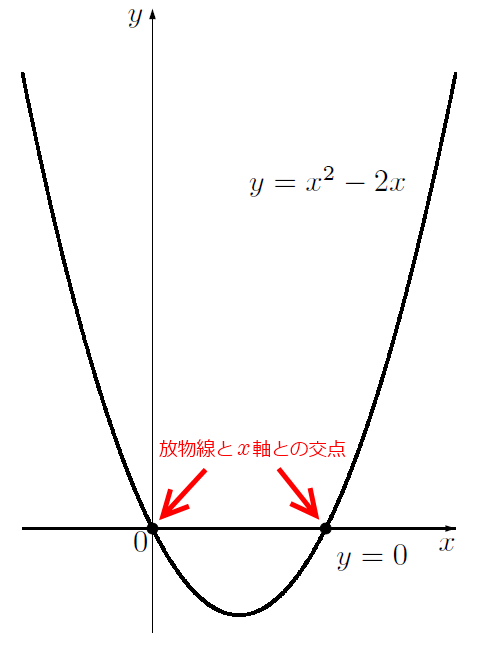
僕「うん、そう。この交点を $(x,y)$ と表したときにもルールがある」

テトラ「ええと……交点であるというルール、ですね？　交わっている点のルール……ええと」

僕「いやいや、そんなに難しく考える必要はないんだよ、テトラちゃん。僕たちはこれまで放物線と $x$ 軸について考えてきた。 点 $(x,y)$ について——」

テトラ「はい、よくわかります」

僕「ではね、点 $(x,y)$ が《放物線 $y=x^2-2x$ と $x$ 軸との交点である》に対応するものは何だと思う？」

テトラ「えっと、交点というのは二つの図形が、ええと、交わってできる点、ですよね。 ですから、こんなふうに、こう……クロスしていて、点ができます」

テトラちゃんは一生懸命ジェスチャつきで説明しようとする。

僕「そうだね。あらためて交点とは何かを答えるのはとても難しいよね」

テトラ「そうなんです……目の前に見えているので、かえって難しくて。ほら、これのこと！　と言いたくなるんです」

僕「じゃあね、まずは次の表現を言い換えてみたらどうかな」

テトラ「言い換える？」

僕「そう、こんなふうに言い換えてみるとわかるかも」

テトラ「……これは、放物線と $x$ 軸の両方の上にあるという意味でしょうか」

僕「そうそう。両方の図形の上にある点。それで交点を説明しているよね」

テトラ「確かに、そうですけれど……いまひとつわからないです」

僕「うん、ここまではまだ《図形の世界》の言葉だからね」

ミルカ「図形の世界？」

ミルカさんさんが急に口をはさんできた。

僕「あ、そうだよ。さっき、《図形の世界》と《数の世界》という言い方で説明してたんだ」

ミルカ「ふうん……もう少しテトラの理解力を信頼してテンポを上げた方がいいな」

ミルカさんはそう言って、自分の《読書の世界》に戻っていった。

僕「それで……《両方の上にある》に対応する【？】は何かを考えてみよう」

テトラ「はい……」

僕「【？】は《$y=x^2-2x$ と $y=0$ の両方が成り立つ》と考えればいい」

テトラ「両方が成り立つ……なるほど！」

僕「うん。 $y=x^2-2x$ という放物線の方程式と、 $y=0$ という $x$ 軸の方程式の両方が成り立つということ」

テトラ「確かにそういえますね」

僕「そうそう。二つの方程式の両方を成り立たせる点が交点だということになる」

ミルカさんが僕をちらっと見る。

テトラ「はい」

僕「ねえ、テトラちゃん」

テトラ「はい何ですか、先輩？」

僕「これで僕たちがよく知っているところまでたどり着いたんだよ」

テトラ「あたしたちがよく知っているところ？」

テトラちゃんは大きな目を見開いてまわりをきょろきょろ見回す。

僕「そう。僕たちはいま二つの方程式の両方を成り立たせる点を見つけたいんだよね。それは、つまり——」

テトラ「つまり？」