![[logo]](https://img.hyuki.net/20220628121544-7a397ed015277339.png) Web連載「数学ガールの秘密ノート」
Web連載「数学ガールの秘密ノート」
この記事は『数学ガールの秘密ノート/式とグラフ』として書籍化されています。
高校二年生の僕は、いとこのユーリに比例と反比例を教えている。 でも、ユーリは反比例のグラフにどうも納得しない。
ユーリ「えー、納得いかなーい!」
僕「どうして? 比例と反比例のグラフはこれでいいんだよ」

ユーリ「だってさ、ぜーんぜん違う形じゃん! 比例は右上がりの直線で、反比例は右下がりの直線のほうがすっきりする」
僕「すっきりするって言われても……わかった。じゃあね、どうして反比例のグラフがこんな形をしているかを説明しよう。 そうすればユーリもきっと納得すると思うよ」
ユーリ「比例が右上がりで増えていって、反比例が右下がりで減っていくなら、なんかちょうどいーじゃん!」
僕「ユーリがちょうどいいように感じても、反比例の定義からはそういうグラフの形にはならないんだよ」
ユーリ「じゃ、反比例の定義はどーゆーの?」
僕「反比例の定義の前に、比例の定義を復習しておこう。まずは比例。それから反比例」
ユーリ「わかったよ、お兄ちゃん。比例の定義……厳密な意味だね」
僕「そうそう」
比例の定義
量 $x$ と、量 $y$ と、 $0$ 以外の定数 $a$ があって、 $$ y = ax $$ という関係がいつも成り立つとする。 このとき、《$y$ は $x$ に比例する》という。
ユーリ「で? 反比例の定義は?」
僕「反比例の定義はこうなる」
反比例の定義
量 $x$ と、量 $y$ と、 $0$ 以外の定数 $a$ があって、 $$ y = \dfrac{a}{x} $$ という関係がいつも成り立つとする。 このとき、《$y$ は $x$ に反比例する》という。
ユーリ「……」
僕「反比例の定義、どう? 意味わかる?」
ユーリ「わかるよ。定数 $a$ があって、 $y$ が $\frac{a}{x}$ ってことでしょ?」
僕「そうそう。それが反比例だね。《$y$ は $x$ に反比例する》は《$x$ と $y$ は反比例の関係にある》ということもあるよ」
ユーリ「あんましピンと来ない」
僕「そう? 比例は $y = ax$ で、反比例は $y = \frac{a}{x}$ だから、式の形がぜんぜんちがうだろ? 反比例の式の特徴は《$x$ が分数の分母に来てる》ってことだね」
ユーリ「まー、式はそーなんだけど……」
僕「何が気になってるの?」
ユーリ「うーん。うまくいえない」
僕「そう。じゃ、少し反比例について話してみよう。反比例のグラフはこんな形になるよ。双曲線という名前がついてる」

ユーリ「……」
僕「《比例のグラフ》は《原点を通る直線》になるけれど、《反比例のグラフ》は《双曲線》になる。式の形がまったく違うから、グラフの形もまったく違うね」
ユーリ「あ!」
僕「ユーリ、どうした?」
ユーリ「そこがね、納得いかないんだよー。グラフの形がぜんぜん違うのに、反対なの?」
僕「反対って……あ、そうか。そこが気になってたんだね」
ユーリ「比例が右上がりで、反比例が右下がりっていうのはまちがいなんでしょ?」
僕「うん、まちがいだね。 原点を通る直線のグラフが右上がりでも右下がりでも、どちらも比例のグラフだよ」
ユーリ「右上がりと右下がりだとちょうど反対っぽいなーって思ったんだけど」
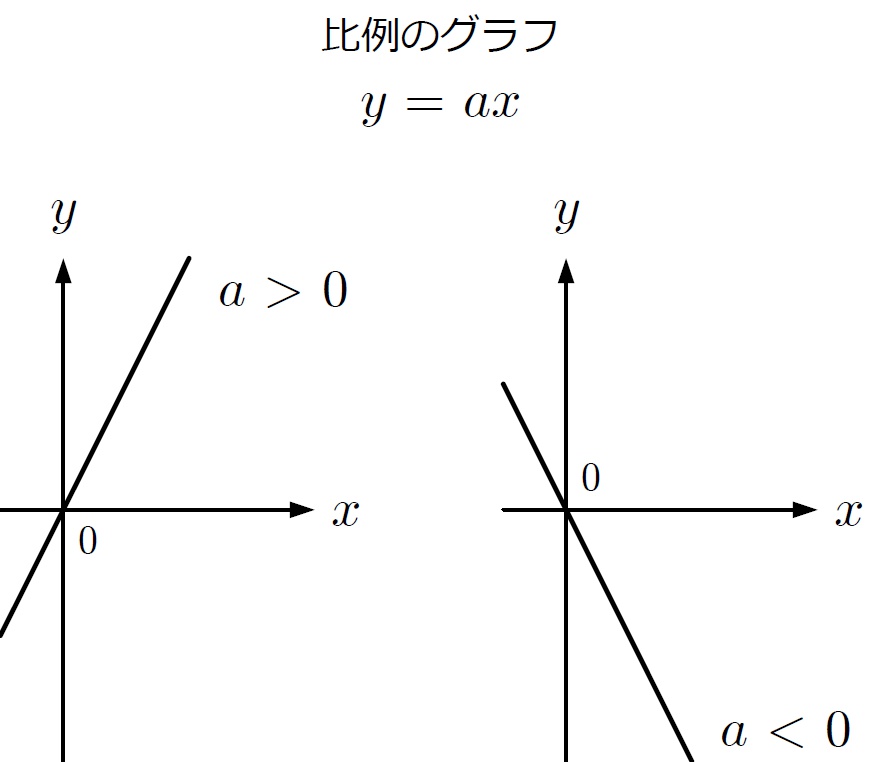
僕「いやいや、ユーリ。雰囲気だけで考えちゃだめだよ。 $y = ax$ という式で、右上がりなら $a > 0$ で、右下がりなら $a < 0$ となる。 つまり、右上がりか右下がりかの違いは、定数 $a$ がプラスかマイナスかの違いなんだ。 $y = ax$ という比例の式はそのまま」
ユーリ「プラスとマイナス……そーゆー種類の反対かー」
僕「うん。ユーリが目を付けた《右上がり》と《右下がり》の違いは《$a > 0$》と《$a < 0$》に対応してたんだね。 その二つは、 $x$ が増えたときに《$y$ が増える》と《$y$ が減る》にちょうど対応している」
$y = ax$ のグラフの形と $a$ の関係
$$ \begin{array}{llll} \REMTEXT{右上がり} & a > 0 & \REMTEXT{$a$はプラス} & \REMTEXT{$x$が増えると$y$は増える} \\ \REMTEXT{右下がり} & a < 0 & \REMTEXT{$a$はマイナス} & \REMTEXT{$x$が増えると$y$は減る} \\ \end{array} $$
ユーリ「うーん、そっか……」
僕「それでね、反比例はまったく違う式の形 $y = \frac{a}{x}$ で定義される」
ユーリ「それそれ! 反対というより、ぜーんぜん違うじゃん!」
僕「確かにそうだね」
ユーリ「そーだよ! 直線と……なんとか曲線」
僕「双曲線」
ユーリ「グラフの形が、直線と双曲線みたいにぜーんぜん違う形なのに」
僕「じゃあね、《式の形》を少し変えてながめてみよう。おもしろいことがわかるよ。うまく《反対》が見つかるから」
ユーリ「へ? 《反対》が見つかるって、どゆこと?」
僕「まずは、比例の式から。いまはちょっと $x \neq 0$ としておく」
$$ \begin{array}{rcll} y &=& ax & \qquad \REMTEXT{比例の式} \\ y \div x &=& a & \qquad \REMTEXT{両辺を$x$で割った($x \neq 0$を仮定)} \\ \end{array} $$ユーリ「これがどーしたの? $y$ を $x$ で割っただけじゃん」
僕「比例の式から $y \div x = a$ という式がでる。この式をじっと見るとわかることがあるよ」
ユーリ「じー」
(比例)この式から、何がわかる?
$$ y \div x = a $$
僕「なにか、わかった?」
ユーリ「なんにも、わかんない」
僕「そう? $y \div x = a$ で、 $a$ は定数だったよね。 だから、《$y$ が $x$ に比例する》とき《$y \div x$ はいつも一定》だということがわかる」
ユーリ「一定ってゆーのは《変わらない》ってことだよね……それだけ?」
僕「そう。ユーリは《それだけ?》っていうけどさ、それってすごいことなんだよ。 $x$ と $y$ は変化する量なのに、《$x$ と $y$ は勝手に変化できない》っていってるんだから」
ユーリ「勝手に変化できない……?」
僕「つまり、 $y \div x$ がいつも一定の値 $a$ になってなくちゃいけないという制約……シバリがあるわけだ」
ユーリ「シバリ?」
僕「そう。縛られている。動けるんだけど、勝手には動けない。完全に自由には動けない」
ユーリ「ふーん」
僕「《$y$ が $x$ に比例する》というとき《$y \div x$ はいつも一定》になってなくちゃいけない。 そういうシバリがあるのが比例」
ユーリ「ま、そー言えないこともないか。シバリね……」
比例では、 $y \div x$ はいつも一定になる
$$ y \div x = a \qquad \REMTEXT{(一定)} $$
僕「そして今度は反比例だよ」
ユーリ「お? そっか、そっちが問題なんだった」
僕「同じように反比例の式を少し変形させてみよう。反比例の式は覚えてる?」
無料で「試し読み」できるのはここまでです。 この続きをお読みになるには「読み放題プラン」へのご参加が必要です。
ひと月500円で「読み放題プラン」へご参加いただきますと、 460本以上の記事がすべて読み放題になりますので、 ぜひ、ご参加ください。
参加済みの方/すぐに参加したい方はこちら
結城浩のメンバーシップで参加 結城浩のpixivFANBOXで参加(2012年12月21日)
この記事は『数学ガールの秘密ノート/式とグラフ』として書籍化されています。
書籍化にあたっては、加筆修正をたくさん行い、 練習問題や研究問題も追加しました。
どの巻からでも読み始められますので、 ぜひどうぞ!