第7回 シーズン1 エピソード7

すなおな反比例（前編）

僕の部屋

ユーリ「ねえ……お兄ちゃん」

僕「何？　ずいぶん眠そうな声してるな」

ユーリ「眠いからだよー。ゆーべゲームしすぎた。頭がすっきりしないー」

僕「ゲーム？」

ユーリ「あー眠い眠い。ところでさ、お兄ちゃん。グラフって何のためにあんの？」

僕「え、グラフって数学のグラフのこと？」

ユーリ「あのね、授業でね、先生が熱心にグラフは大事だ！　グラフは大事だ！　ってゆーんだけど、 《なんでグラフが大事か》はさっぱり教えてくれないんだよ。そんで、何のためにあんのかにゃって」

ユーリは急に甘えた猫語になった。

僕「なるほど。ところで、ユーリはグラフってどういうものか知ってる？」

ユーリ「バカにしないでほしいにゃあ……」

僕「してないよ。グラフといってもいろいろあるからね」

ユーリ「ん？　たとえばこーゆーの」

僕「これはなに？」

ユーリ「折れ線グラフじゃん！」

僕「これはちょっと折れ線グラフとはいえないなあ。 ちゃんとした折れ線グラフにするには、こんな風にしなくちゃ」

ユーリ「大して違わないじゃん」

僕「ぜんぜん違うよ」

• $x$ と $y$ のように軸（じく）に名前を付けている
• 軸に目盛りを付けている

ユーリ「ふーん」

僕「ここでは $x$ と $y$ って名前を付けたけど、 グラフを書いたり読んだりするときは、 横軸が何を表していて、 縦軸が何を表しているかを確認するのはとっても大切なんだよ」

ユーリ「はいはい。わかったよ」

僕「ともかく、グラフは確かに大事だよね」

ユーリ「だーかーらー！　グラフがなぜ大事かをさっきから聞いてんじゃん」

僕「だって、グラフを見れば変化を読み取れるからね」

ユーリ「あ、それそれそれそれ。先生もね、グラフから読み通れるって言ってた」

僕「読み通れるじゃなくて《読み取れる》だよ」

ユーリ「何でもいいけど、グラフはグラフじゃん。言葉が書いてないのに、読み取るっていうのはどゆこと？」

僕「そうだなあ……何か変化する数や量があるとするよね」

ユーリ「変化する数や量って？」

僕「たとえば、ユーリの体重とか」

ユーリ「お兄ちゃん！　女性に向かってそーゆー話題を出すのは命知らずだよ」

僕「命知らず……じゃあ、気温にしようか。こういう気温の変化を表す折れ線グラフはよくある」

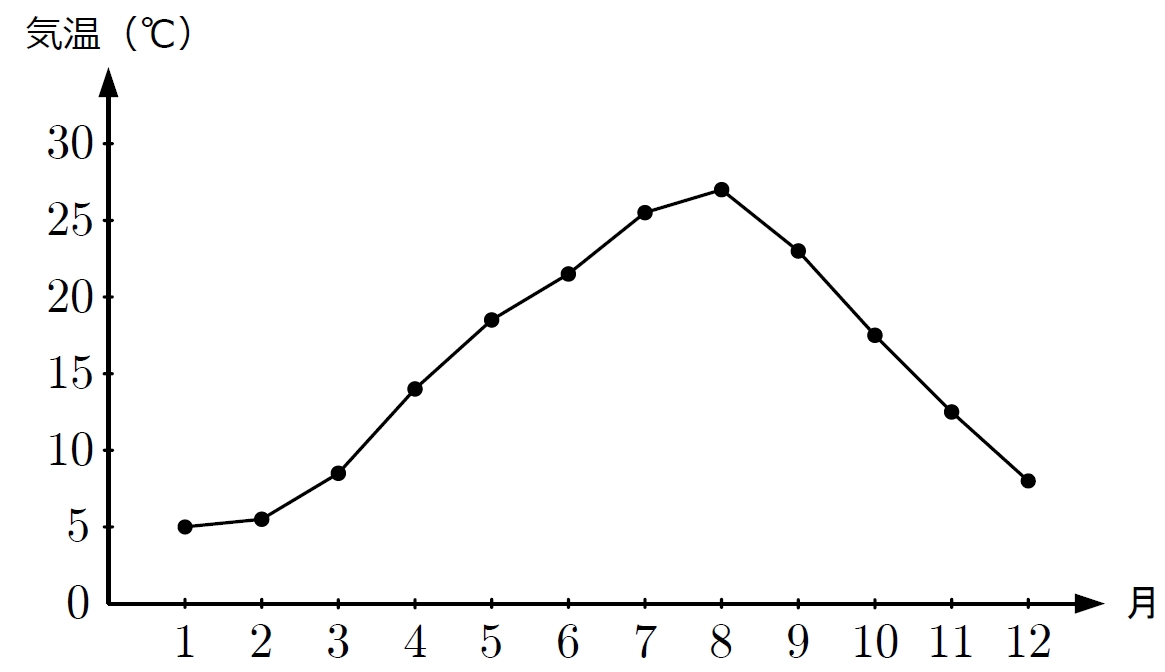
ユーリ「これがどーしたの？」

僕「この折れ線グラフを見ると、夏になると気温が上がって、冬になると下がることがよくわかる」

ユーリ「そんなのあたりまえじゃん。夏は暑いし、冬は寒いよ」

僕「そうだね。気温が変化する様子が《グラフの形》からわかるわけだよね。 このグラフの形をよく見ると、8月のところが一番高くなってる。ということは8月が一番暑いんだなということがわかる。 そんなふうに《グラフの形を見てどんな意味か考える》ことを《グラフから読み取る》っていうんだよ」

ユーリ「グラフの形を見て……どんな意味か考える？」

僕「うん、ほら、《文章を見てどんな意味か考える》ことを《文章から読み取る》っていうのと同じことだよ」

ユーリ「ふーん」

僕「そうだ。グラフでは単位（たんい）も大事だね。ほら気温のところに℃て単位が書いてあって……」

ユーリ「ま、それはさておき」

僕「さておくなよ」

ユーリ「あのね、グラフから読み取らなくても、夏が暑いし冬が寒いのはあたりまえじゃん？」

僕「じゃ、このグラフからは何が読み取れるかな」

ユーリ「ほよ！　このグラフだと、夏が寒くて冬が暑い。おかしー！」

僕「そうだね。さむがなつくてあつがふゆい」

ユーリ「お兄ちゃんはギャグが寒い」

僕「これはシドニーの気温の折れ線グラフなんだ。 シドニーは南半球のオーストラリアにあるから、北半球にある日本とは気温の変化が逆転するんだ。 グラフを見ると夏……というか7月が最も寒くなっているのがよくわかるね」

ユーリ「ふーん、そういうのが……グラフから読み取れること？」

僕「そう。グラフから読み取れることは他にもたくさんあるけどね」

ユーリはポニーテールの髪の先をいじりながら、何かを考え始めた。

ユーリ「……えー、でもさ、グラフを見ても7月の気温が何℃なのかは、バシっとわかんないよ。 だいたい……ええと、12℃ぐらいってはわかるけど」

僕「確かにそうだね。ユーリのいう通りだ。 この折れ線グラフだとそういう精密な数値を読み取るのは確かに難しい。 正確な数値を知りたいなら、表（ひょう）になっている方がわかりやすい」

東京とシドニーの気温の表（単位は℃）

$$ \begin{array}{|c|rrrrrrrrrrrr|} \hline \textbf{都市} & 1月 & 2月 & 3月 & 4月 & 5月 & 6月 & 7月 & 8月 & 9月 & 10月 & 11月 & 12月 \\ \hline \textbf{東京} & 5.2 & 5.6 & 8.5 & 14.1 & 18.6 & 21.7 & 25.2 & 27.1 & 23.2 & 17.6 & 12.6 & 7.9 \\ \hline \textbf{シドニー} & 22.6 & 22.7 & 21.4 & 18.8 & 15.7 & 13.1 & 12.2 & 13.2 & 15.5 & 18.0 & 19.7 & 21.7 \\ \hline \end{array} $$

ユーリ「そっか。表だと7月の東京は……えっと25.2℃で、シドニーは12.2℃ってわかるね」

僕「それは表から読み取っているわけだね」

ユーリ「ふーん」

僕「つまりね、グラフは全体の形を調べるのに向いていて、 表は個別の数値を精密に調べるのに向いていることになる。 グラフと表は、それぞれ向き不向きがあることになるね」

ユーリ「まー、そこまではわかったけど」

比例

僕「気温じゃなくて、もっと数学的なグラフの話をしようか」

ユーリ「数学的なグラフ？」

僕「ユーリは比例（ひれい）っていう言葉を聞いたことがある？」

ユーリ「あるよ、もちろん。《比例する》ってよくゆーじゃん。《ナントカに比例して大きくなる》とか」

僕「そうだね。それじゃユーリに聞くけど、比例という言葉の定義（ていぎ）を知ってる？」